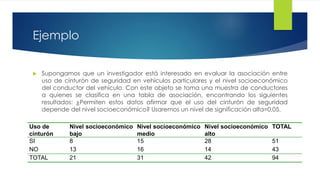
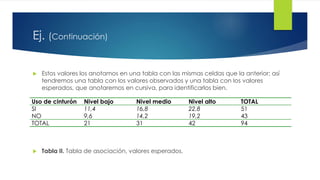
Este documento presenta diferentes pruebas de hipótesis para analizar datos estadísticos, incluyendo pruebas para medias, proporciones, diferencias entre medias y proporciones, y la prueba de chi-cuadrado. También incluye un ejemplo completo de cómo aplicar la prueba de chi-cuadrado para determinar si el uso de cinturón de seguridad depende del nivel socioeconómico usando datos de una muestra.

1. Pruebas de Hipótesis
ESPINOZA GRACIA JORGE ARMADO
GAMBOA CORONEL JOEL
MEDINA PADILLA SARAH ELIZABETH

2. Media con muestras grandes
 Cuando la prueba de la media poblacional proviene de una muestra grande y la
desviación estándar poblacional es conocida, el estadístico de la prueba se obtiene
con la siguiente fórmula:
 Cuando σ es desconocida la estimamos con la desviación estándar de la muestra s.
Mientras el tamaño de muestra n > 30, z se puede aproximar con:
z
X

 
 / n
z
X
s n

 
/

3. Media con muestras pequeñas
 El estadístico de la prueba es la distribución t. El estadístico de la prueba para el
caso de una muestra es:
ns
X
t
/



4. Proporción poblacional
 Una proporción poblacional es simplemente una media poblacional para una
población de 0 y 1: una población de Bernoulli.
n
pp
pp
z
00
0
1(
ˆ




5. Diferencia entre dos medias con
muestras grandes
 Los datos los conformarán dos muestras, una para cada población. La idea básica
es simple. Se calculará la diferencia de las medias muestrales. Si la diferencia se
encuentra alejada de 0, se concluirá que las medias poblacionales son diferentes. Si
la diferencia se aproxima a 0, se concluirá que las medias poblacionales podrían ser
iguales
   
y
y
x
x
yx
nn
yx
z 22






6. Diferencia entre dos medias con
muestras chicas
 Se asume que las 1 y 2 son iguales pero desconocidas:
 Se asume que las 1 y 2 son desiguales y desconocidas:
2
2
1
2
2121
21
2
2
21
2
12 )()(
;
2
)1()1(
n
S
n
S
XX
t
nn
nSnS
S
pp
cp







2
2
2
1
2
1
2121 )()(
'
n
S
n
S
XX
t c





7. Diferencia entre dos proporciones
 El objetivo de estas pruebas de hipótesis es determinar si las dos muestras
independientes fueron tomadas de diferentes poblaciones que
presentan la misma proporción de elementos con cierta característica.
 Las hipótesis que se pueden establecer con estas pruebas son:
 𝐻0: 𝑝1 − 𝑝2 = 0
 𝐻1: 𝑝1 − 𝑝2 ≠ 0
 𝐻1: 𝑝1 − 𝑝2 > 0
 𝐻1: 𝑝1 − 𝑝2 < 0

8.  La fórmula para calcular el valor estadístico de prueba es:
 Siendo:
x
x
n
x
p ˆ
)
11
)(ˆ1(ˆ
ˆˆ
yx
yx
nn
pp
pp
Z



y
y
n
y
p ˆ
yx nn
yx
p


ˆ

9. Diferencia con datos apareados
 La idea básica para la construcción de este tipo de pruebas de hipótesis es la
colección de diferencias como una sola muestra aleatoria de una población de
diferencias.
 El valor del estadístico de prueba se calcula como:
 Con
 Siendo 𝐷 la media de las diferencias de las 2 muestras y utilizando la tabla t-student.

0
 D
t
n
s


10. Chi- Cuadrada
 Esta prueba puede utilizarse incluso con datos medibles en una escala nominal. La
hipótesis nula de la prueba Chi-cuadrado postula una distribución de probabilidad
totalmente especificada como el modelo matemático de la población que ha
generado la muestra.
 Para realizar este contraste se disponen los datos en una tabla de frecuencias.
Para cada valor o intervalo de valores se indica la frecuencia absoluta observada
o empírica



k
i
i
ii
E
Eo
x 1
2
2 )(

11. Ejemplo
 Supongamos que un investigador está interesado en evaluar la asociación entre
uso de cinturón de seguridad en vehículos particulares y el nivel socioeconómico
del conductor del vehículo. Con este objeto se toma una muestra de conductores
a quienes se clasifica en una tabla de asociación, encontrando los siguientes
resultados: ¿Permiten estos datos afirmar que el uso del cinturón de seguridad
depende del nivel socioeconómico? Usaremos un nivel de significación alfa=0,05.
Uso de
cinturón
Nivel socioeconómico
bajo
Nivel socioeconómico
medio
Nivel socioeconómico
alto
TOTAL
SI 8 15 28 51
NO 13 16 14 43
TOTAL 21 31 42 94

12. Ej. (Continuación)
1. En primer lugar se debe plantear las hipótesis
que someteremos a prueba
 H0: “El uso de cinturón de seguridad es
independiente del nivel socioeconómico”.
 H1: “El uso de cinturón de seguridad depende
del nivel socioeconómico”.
2. En segundo lugar, obtener (calcular) las
frecuencias esperadas
 Las frecuencias esperadas se obtendrán de la
distribución de frecuencias del total de los
casos, 51 personas de un total de 94 usan el
cinturón y 43 de 94 no lo usan. Esa misma
proporción se debería dar al interior de los tres
grupos de nivel socioeconómico, de manera
que el cálculo responde al siguiente
razonamiento: si de 94 personas 51 usan
cinturón; de 21 personas, ¿cuántas debieran
usarlo?
Nivel bajo: (21x51/94)=11.4-(21x43/94)= 9.6
Nivel medio: (31x51/94)=16.8-(31x43/94)= 14.2
Nivel alto: (42x51/94)=22.8-(42x43/94)= 19.2

13. Ej. (Continuación)
 Estos valores los anotamos en una tabla con las mismas celdas que la anterior; así
tendremos una tabla con los valores observados y una tabla con los valores
esperados, que anotaremos en cursiva, para identificarlos bien.
 Tabla II. Tabla de asociación, valores esperados.
Uso de cinturón Nivel bajo Nivel medio Nivel alto TOTAL
SI 11,4 16,8 22,8 51
NO 9,6 14,2 19,2 43
TOTAL 21 31 42 94

14. Ej. (Continuación)
3. En tercer lugar se debe calcular el estadístico de prueba
 Uso de tabla ji-cuadrado
 La tabla de ji-cuadrado tiene en la primera columna los grados de libertad y en la
primera fila la probabilidad asociada a valores mayores a un determinado valor del
estadístico
 Grados de libertad (gl)=(nº de filas–1)x(nº de columnas–1)
Así, en nuestro ejemplo, en que hay 2 filas y 3 columnas, los grados de libertad serán:
gl=(2-1)x(3-1)=2
23.5
2.19
)2.1914(
8.22
)8.2228(
2.14
)2.1416(
8.16
)8.1615(
6.9
)6.913(
4.11
)4.118()( 2222222
2














 
i
ii
e
eo
x

15. Ej. (Continuación)
 Al comienzo elegimos un nivel de significación alfa=0,05. Entonces un valor de tabla
para x2 asociado a 2 grados de libertad y alfa 0,05 es 5,99.
 Por lo tanto, como en el gráfico 2 vemos que 5,23 se encuentra a la izquierda de 5,99,
la probabilidad asociada a valores superiores a 5,23 es mayor que alfa (0,05).

16. Ej. (Continuación)
 Según esto, debemos aceptar la hipótesis nula que plantea que las
variables “uso de cinturón de seguridad” y “nivel socioeconómico” son
independientes. Limitación: como norma general, se exige que el 80% de
las celdas en una tabla de asociación tengan valores esperados mayores
de 5.