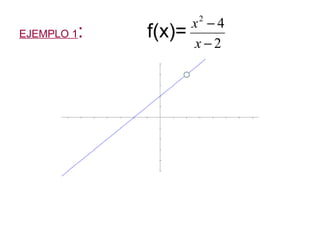
El documento presenta 4 ejemplos de funciones racionales y analiza su continuidad y tipo de discontinuidades en puntos donde anula el denominador. El primer ejemplo muestra una discontinuidad evitable. El segundo y tercer ejemplo presentan discontinuidades salto infinito. El cuarto ejemplo analiza discontinuidades salto infinito en dos puntos y tiene una asíntota horizontal.

1. LÍMITES DE FUNCIONES
CONTINUIDAD
EJEMPLOS
Aurora Domenech

2. EJEMPLO 1
:
f(x)=
x −4
x−2
2

3. EJEMPLO 1
x −4
f(x)= x − 2
2
:
Es una función racional.
Su dominio son todos los reales excepto x=2 que anula el
denominador.
Es continua en todo su dominio.
Analizamos el tipo de discontinuidad en x=2
¿Existe f(2)?
¿Existe el límite de la
función en x=2?
¿Coinciden límite
e imagen?
Tipo de discontinuidad:
f (2) =
0
0
in det er min ación
No existe
( x + 2)( x − 2) = lim( x + 2) = 4
x2 − 4 0
lim
= = lim
x→2 x − 2
x→2
0 x→2
x−2
Evidentemente, no; ya que uno de ellos no
existe
“falta un punto” discontinuidad
evitable en x=2.

4. EJEMPLO 2
:
x +x
f ( x) = 3
2
x − 2x + x
2

5. EJEMPLO 2
:
x +x
f ( x) = 3
2
x − 2x + x
2
Es una función racional.
Su dominio son todos los reales excepto x=0 y x=1 que anulan el
denominador.
Es continua en todo su dominio.
Analizamos el tipo de discontinuidad en x=0
¿Existe f(0)?
¿Existe el límite de la
función en x=0?
¿Coinciden límite
e imagen?
Tipo de discontinuidad:
f ( 0) =
0
0
in det er min ación
No existe
x2 + x
0
x·( x + 1)
( x + 1) 1
lim 3
= = lim
= lim
= =1
x →0 x − 2 x 2 + x
x →0 x·( x − 1) 2
x →0 ( x − 1) 2
0
1
Evidentemente, no; ya que uno de ellos no
existe
“falta un punto” discontinuidad
evitable en x=0.

6. EJEMPLO 2
:
x +x
f ( x) = 3
2
x − 2x + x
2
Analizamos ahora el tipo de discontinuidad en x=1
¿Existe f(1)?
¿Existe el límite de la
función en x=1?
f (1) =
2
0
x2 + x
2
lim 3
=
x →1 x − 2 x 2 + x
0
No existe
Obligatoriedad
de estudiar
límites laterales
x2 + x
2
lim 3
= + = +∞
2
x →1+ x − 2 x + x
0
Asíntota vertical en x=1
x +x
2
= + = +∞
x3 − 2x 2 + x 0
2
lim
−
x →1
¿Coinciden límite
e imagen?
Tipo de discontinuidad:
Evidentemente, no.
discontinuidad salto infinito en x=1.

7. EJEMPLO 3:
x +1
f ( x) =
x −1
2

8. x2 +1
EJEMPLO 3: f ( x ) =
x −1
¿Existe f(1)?
Es una función racional.
Su dominio son todos los reales
excepto x=1 que anula el denominador.
Es continua en todo su dominio.
Analizamos el tipo de discontinuidad en x=1
12 + 1 2
f (1) =
=
No existe
1−1 0
¿Existe el límite de la
función en x=1?
x2 +1 2
lim
=
x →1 x − 1
0
Obligatoriedad
de estudiar
límites laterales
x2 +1 2
lim
= + =∞
+
x →1 x − 1
0
x +1 2
=
= −∞
x − 1 0−
2
lim
−
x →1
Tipo de discontinuidad:
Asíntota vertical en x=1
discontinuidad salto infinito en x=1.

9. x2 +1
EJEMPLO 3: f ( x ) =
x −1
Es una función racional.
Como el grado del numerador es uno
mayor que el del denominador existirá
una asíntota oblicua. Vamos a calcularla.
Asíntota oblicua es del tipo y=mx+n
f ( x)
x2 +1
x2
m = lim
= lim 2
≈ lim 2 = 1
x →∞
x →∞ x − x
x →∞ x
x
 x2 +1

 x2 +1

2
n = lim[ f ( x) − m· x ] = lim 
− 1· x  ≈ lim 
− 1· x  = lim
=0
x →∞
x →∞ x − 1
x →∞ x − 1
x →∞ x − 1




Asíntota oblicua es y=x

10. EJEMPLO 4
x2 − 4
f ( x) = 2
x −1

11. EJEMPLO 4
x2 − 4
f ( x) = 2
x −1
Es una función racional cuyo dominio son todos los reales
excepto el 1 y el -1.
Analizamos el tipo de discontinuidad en esos dos puntos.
Análisis de continuidad en x=-1
¿Existe f(-1)?
¿Existe el límite de la
función en x= -1?
( − 1) 2 − 4 = − 3
f (−1) =
( − 1) 2 − 1 0
x2 − 4 − 3
lim 2
=
x → −1 x − 1
0
No existe
Obligatoriedad
de estudiar
límites laterales
x2 − 4 − 3
lim+ 2
= − = +∞
x → −1 x − 1
0
x −4 −3
=
= −∞
x 2 − 1 0+
2
lim−
x → −1
Tipo de discontinuidad:
Asíntota vertical en x= - 1
discontinuidad salto infinito en x= -1.

12. EJEMPLO 4
x2 − 4
f ( x) = 2
x −1
Es una función racional cuyo dominio son todos los reales
excepto el 1 y el -1.
Analizamos el tipo de discontinuidad en esos dos puntos.
Análisis de continuidad en x=1
¿Existe f(1)?
¿Existe el límite de la
función en x= 1?
(1) 2 − 4 = − 3
f (1) = 2
(1) − 1 0
x2 − 4 − 3
lim 2
=
x →1 x − 1
0
No existe
Obligatoriedad
de estudiar
límites laterales
x2 − 4 − 3
lim 2
= + = −∞
+
x →1 x − 1
0
x −4 −3
=
= +∞
x 2 − 1 0−
2
lim
−
x →1
Tipo de discontinuidad:
Asíntota vertical en x= 1
discontinuidad salto infinito en x= 1.

13. EJEMPLO 4
x −4
f ( x) = 2
x −1
2
Al tener el mismo grado numerador y denominador, existirá una asíntota
horizontal.
x2 − 4
x2
lim f ( x) = lim 2
≈ lim 2 = 1
x →∞
x →∞ x − 1
x →∞ x
x2 − 4
x2
lim f ( x) = lim 2
≈ lim 2 = 1
x → −∞
x → −∞ x − 1
x → −∞ x
Por lo tanto la recta y=1 es una asíntota horizontal