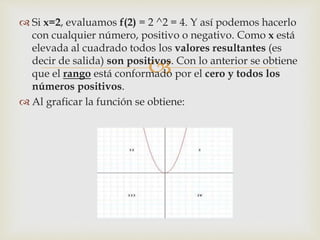
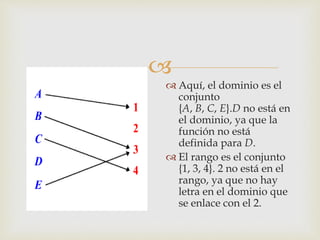
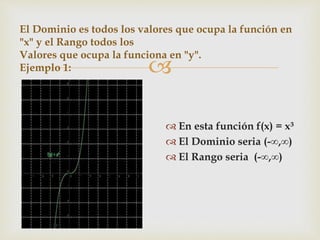
Este documento contiene información sobre funciones reales, dominio y rango. Define una función real como una función definida de un subconjunto de números reales al conjunto de números reales. Explica que el dominio de una función es el conjunto de valores que puede tomar la variable independiente, mientras que el rango es el conjunto de valores que puede tomar la variable dependiente al evaluar la función. Proporciona ejemplos como ilustración.

1. Integrantes:
Norman Eras
Michelle Escobar
Marlene Guacho

2. 
 Se llama función real a toda función definida de un
subconjunto D de los números reales, en el
conjunto R de los números reales, tal que a cada
elemento x de D le corresponde uno y sólo un
elemento y.
Que es una variable
real?

3.  Tiene por conjunto origen o campo de existencia todos
los números reales, pues dado cualquier número real x,
siempre es posible calcular su cuadrado, siendo el
resultado otro número real.

 Tiene por conjunto imagen todos los números reales
positivos, puesto que el cuadrado de un número
siempre es positivo:

 La regla de asignación es «dado cualquier número
real x, calcular su cuadrado para obtener la imagen».

4. 
 Está dado por el conjunto de valores que puede tomar
una función. Por ejemplo si f(x) = x; esta
variable x puede tomar cualquier valor, no tiene
ninguna restricción, entonces su dominio esta
compuesto por todos los números Reales.
 Como los valores de la función están dados para la
variable independiente (x), los valores que puede tomar
la función son aquellos para los cuales al evaluar la
función para un valor de x, su resultado nos da un
número Real. Por ejemplo la función:
 f(x) =
Dominio

5. 
 En general se pueden seguir las siguientes
recomendaciones para obtener el dominio de una
función o de una expresión algebraica:
 No puede haber una raíz cuadrada ( ó cualquier raíz
par ) negativa, pues se trataría de un número
imaginario que no hace parte de los Reales.
 Un fraccionario no puede contener por denominador
cero, pues la expresión queda indeterminada.

6. 
 Está determinado por todos los valores que pueden
resultar al evaluar una función. Son los valores
obtenidos para la variable dependiente (y). También
se puede expresar como todos los valores de salida
de la función.
Rango

7. 
 Si x=2, evaluamos f(2) = 2 ^2 = 4. Y así podemos hacerlo
con cualquier número, positivo o negativo. Como x está
elevada al cuadrado todos los valores resultantes (es
decir de salida) son positivos. Con lo anterior se obtiene
que el rango está conformado por el cero y todos los
números positivos.
 Al graficar la función se obtiene:

8. 
 Aquí, el dominio es el
conjunto
{A, B, C, E}.D no está en
el dominio, ya que la
función no está
definida para D.
 El rango es el conjunto
{1, 3, 4}. 2 no está en el
rango, ya que no hay
letra en el dominio que
se enlace con el 2.

9. 
El Dominio es todos los valores que ocupa la función en
"x" y el Rango todos los
Valores que ocupa la funciona en "y".
Ejemplo 1:
 En esta función f(x) = x³
 El Dominio seria (-∞,∞)
 El Rango seria (-∞,∞)

10. 
GRACIAS POR SU
ATENCIÓN.