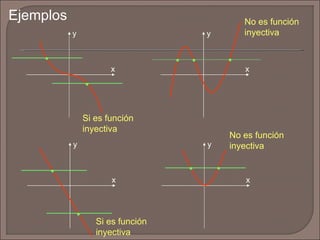
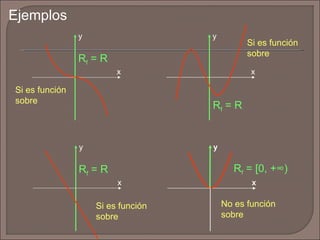
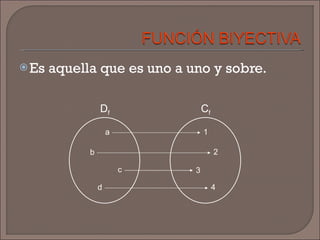
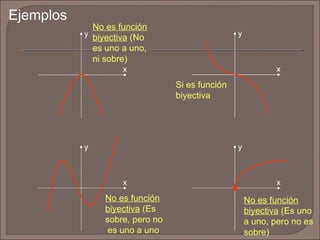
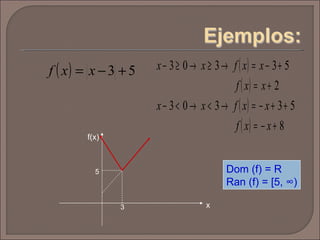
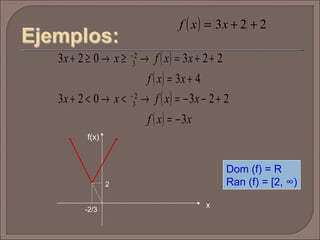
El documento define las funciones inyectivas, sobreyectivas y biyectivas y proporciona ejemplos de cada una. También define la función valor absoluto, su dominio y rango, y muestra cómo graficarla. Finalmente, pide graficar otra función especificada y determinar su dominio y rango.

1. Srta. Yanira Castro Lizana (según el tipo de correspondencia)

2. Uno a uno (Inyectiva) Sobre (Suprayectiva) Biyectiva

3. Es aquella en la que a elementos distintos del Dominio le corresponden elementos distintos del Codominio. No importa que elementos del Codominio no sean imágenes del Dominio. a b c d 1 2 3 4 5 D f C f O sea, dos o más elementos del Dominio, no pueden tener la misma imagen; y el Rango de la función, no tiene que ser igual al Codominio.

4. Puesto que a cada elemento distinto del Dominio de una función debe de corresponder un elemento distinto del Codominio, ninguna recta horizontal puede cortar la gráfica cartesiana de una función INYECTIVA en más de un punto.

5. Si es función inyectiva No es función inyectiva Si es función inyectiva No es función inyectiva Ejemplos y x • • y x • • x y • • y x • • •

6. Es aquella en la que a todo elemento del Codominio le corresponde cuando menos un elemento del Dominio. a b c d 1 2 3 4 D f C f e O sea, el Rango de la función, tiene que ser igual al Codominio. En el caso de una función real de variable real, el Rango debe ser igual al conjunto de los números reales R.

7. Si es función sobre No es función sobre Si es función sobre Si es función sobre Ejemplos x y R f = R y x R f = R y x R f = R y x R f = [0, + ∞) y x

8. Es aquella que es uno a uno y sobre. a b c d 1 2 3 4 D f C f

10. Ejemplos y x • No es función biyectiva (No es uno a uno, ni sobre) No es función biyectiva (Es uno a uno, pero no es sobre) No es función biyectiva (Es sobre, pero no es uno a uno Si es función biyectiva y x y x y x

13. En algunos casos, nos puede interesar conocer la diferencia entre los datos recogidos y un número en particular, sin importar que esta diferencia es positiva o negativa. Por ejemplo, podemos obtener la distancia de los siguientes puntos al valor de 2: Distancia: |x – 2| 2 3 5 9 0 -2 x

14. Definición de Valor Absoluto. Identificación de la función valor absoluto, su dominio y rango. Gráfica de la función valor absoluto en el plano.

15. |15| = 15 |-4| = -(-4) = 4

16. Dom (f) = R Ran (f) = [0, ∞) x f(x)

17. En términos generales: h k Dom (f) = R Ran (f) = [k, ∞) Es posible deducir la siguiente gráfica con la técnica de traslación: x f(x)

18. Dom (f) = R Ran (f) = [5, ∞) 3 5 x f(x)

19. x f(x) Dom (f) = R Ran (f) = [2, ∞) -2/3 2

20. Grafique la siguiente función, determinando su dominio y rango.