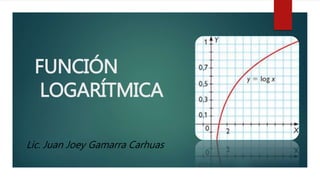
Este documento describe la función logarítmica, que es una función importante en matemáticas y un poderoso instrumento para el cálculo numérico. La función logarítmica es la recíproca de la función exponencial y aparece en fenómenos como el crecimiento de bacterias y la desintegración radiactiva. El documento también define formalmente la función logarítmica, describe algunas de sus propiedades clave y teoremas y aplicaciones de ecuaciones e inecuaciones logarítmica

1. FUNCIÓN
LOGARÍTMICA
Lic. Juan Joey Gamarra Carhuas

2. La función logarítmica es muy importante
en matemáticas. Constituye un poderoso
instrumento en la práctica del cálculo
numérico.
Por ser la recíproca de la exponencial, esta
función es una de las de más presencia en
los fenómenos observables.
Así aparece en la reproducción de una
colonia de bacterias, la desintegración de
una sustancia radiactiva, algunos
crecimientos demográficos, la inflación, la
capitalización de un dinero colocado a
interés compuesto, etc.
I N T R O D U C CI ÓN
FUNCIÓN
LOGARÍTMICA

3. FUNCIÓN LOGARÍTMICA
La función logarítmica con base 푏 > 0; 푏 ≠ 1, se
define así
퐷표푚 푓 = 0; +∞
푅푎푛 푓 = ℝ
Donde:
FUNCIÓN
LOGARÍTMICA
푓 푥 = log푏 푥

4. PROPIDADES
1. La función 푓 es decreciente para 0 < 푏 < 1 y
creciente para 푏 > 1.
FUNCIÓN
LOGARÍTMICA
0 < 푏 < 1 푏 > 1

5. PROPIDADES
FUNCIÓN
LOGARÍTMICA
2. La gráfica de la función 푓 pasa por el punto 푃 1; 0

6. TOREMAS DE ECUACIONES LOGARÍTMICAS
푏 > 0; 푏 ≠ 1
log푏 푁 = 푦 ↔ 푁 = 푏푦
FUNCIÓN
LOGARÍTMICA
푏 > 0; 푏 ≠ 1
log푏 퐴 = log푏 퐵 ↔ 퐴 = 퐵
APLICACIONES

7. TOREMAS DE INECUACIONES LOGARÍTMICAS
0 < 푏 < 1
log푏 푥 < log푏 푦 ↔ 푥 > 푦
푏 > 1
log푏 푥 < log푏 푦 ↔ 푥 < 푦
APLICACIONES
FUNCIÓN
LOGARÍTMICA