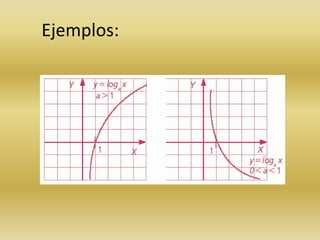
La función logarítmica relaciona un número con el exponente a la que debe elevarse una base para obtener ese número. Las propiedades de los logaritmos incluyen que la base no puede ser negativa, no se pueden hallar logaritmos de números negativos, y el logaritmo de la potencia de un número es el producto del exponente por el logaritmo de la base. La función logarítmica depende de si la base es mayor o menor que uno, y es la función inversa de la exponencial para esa base.

1. Función Logarítmica
Arroyo Nahuel, Cáneva Victoria,
Murga Franco, Ruiz Carolina. 4º 1º
HUMANIDADES

2. Definición de Logaritmo:
• El logaritmo de un numero respecto a otro
llamado base es el exponente a que hay que
elevar la base para obtener dicho numero.
2² = 4
2³ = 8

3. • Diremos que siendo 2 la base en todos los
casos, el logaritmo de 4 es 2 puesto que 2 es
el exponente a que se debe elevar la base 2
para obtener el numero 4.
Log 4 = 2
2

4. Logaritmo

5. Propiedades de los logaritmos:
• La base de un sistema de logaritmos no puede ser un numero
negativo.
• No pueden hallarse logaritmos de un numero negativo.
• El logaritmo de la base es siempre igual a la u.
• En cualquier sistema de logaritmos, el logaritmo de la unidad
es cero.
• El logaritmo de un cociente coincide con la diferencia entre el
logaritmo del dividendo y del divisor.
• El logaritmo de una potencia coincide con el producto del
exponente por el logaritmo de la base.

6. Logaritmo de un numero
En la función y = log x …
²
• Al realizar la tabla correspondiente tendremos
que: A x=8 le corresponde y=3
A x=1 le corresponde y=0
A x=1/2 le corresponde y=-1

7. Propiedades de la función logarítmica
• En el caso de la función logarítmica, el
argumento debe ser siempre mayor a cero (x>0)
• Dependiendo de la base, si es mayor a uno, o
menor a uno, la curva graficada tendrá una
determinada posición
• La función logarítmica en base a es la función
inversa de la exponencial en base a… f(x)=loga
x / a>0 a‡1
• Creciente si a>1.
• Decreciente si a<1.

8. Ejemplos:

9. f(x) = Log2 (x+8)
• El dominio de la función es el conjunto de aquellos
valores que permiten que ella exista (los números
mayores que -8) (después de resolver x+8)
• Las intersecciones con el eje Y se obtienen haciendo
x = 0 y resolviendo:
f(x) = Log_2(x + 8)
f(0) = Log_2(0 + 8)
f(0) = Log_2(8) / 2³ = 8 / La función corta el eje Y
en (0, 3)
(Ejemplo para encontrar dominio e intersecciones)