Este documento explica la función seno inversa. Indica que las funciones trigonométricas no tienen inversas debido a que son periódicas y no inyectivas, pero se puede hallar la inversa restringiendo los dominios. Explica que la función seno inversa, denotada sen-1(x), tiene como dominio [-1,1] y como recorrido [-π/2, π/2]. Presenta ejemplos y gráficas de la función seno inversa obtenidas mediante software.

1. Fundamentos Matemáticos
UTPL
UNIVERSIDAD TÉCNICA PARTICULAR DE LOJA
Fundamentos Matemáticos
Alumno: Carlos Leonardo Quizhpe Palacios.
Ciclo: 5to ciclo
Paralelo: “B”
Fecha: 08/11/2013

2. Fundamentos Matemáticos
UTPL
Función Seno Inversa
Son necesarias para calcular los ángulos de un triángulo a partir de la medición de
sus lados, aparecen con frecuencia en las soluciones de ecuaciones diferenciales.
Sin embargo ninguna de las 6 funciones trigonométricas básicas tiene inversa
debido a que son funciones periódicas y por lo tanto no son inyectivas pero
restringiendo los dominios se puede hallar la inversa.
La función y = sen x no es uno a uno en su dominio natural porque al trazar
cualquier recta horizontal corta la gráfica en más de un punto
El condominio es [-1, 1], su grafica es:
Fig.1.- Figura muestra la gráfica de una función seno.
Imagen tomada de un software de simulación.
F(x)=sen x en el intervalo [
−𝜋
2
,
𝜋
2
] es creciente y por lo tanto inyectiva es decir existe
la inversa su dominio [
−𝜋
2
,
𝜋
2
] y el recorrido es [-1, 1] y su graficas seria la siguiente:

3. Fundamentos Matemáticos
UTPL
Fig.2.- Figura muestra la gráfica de un intervalo de una función seno.
Imagen tomada de un software de simulación.
Si y = sen x entonces la inversa se nota y = arc sen x o también se nota 𝑦 = 𝑠𝑒𝑛−1 𝑥.
La función inversa de y = sen x restringido es: 𝑦 = 𝑠𝑒𝑛−1 𝑥 su dominio es [-1,1] y el
recorrido [
−𝜋
2
,
𝜋
2
], es un grafica creciente y una función impar.
Fig.3.- Figura muestra la gráfica de una función arco seno o inversa del seno.
Imagen tomada de un software de simulación.
Ejemplo:
Evaluar la siguiente función:
y=𝑠𝑒𝑛−1
(√
3
2
)

4. Fundamentos Matemáticos
UTPL
Fig.4.- Figura muestra la gráfica del ejercicio propuesto.
Imagen tomada de un software de simulación en línea.
Ejercicio realizado en matlab.
Código
Grafica
x=-1:0.01:1;
f=asin(x)
plot(x,f)
title('Funcion Arcoseno')
xlabel('x')
ylabel('asin(x)')
grid on

5. Fundamentos Matemáticos
UTPL
Fig.5.- Figura muestra la gráfica del ejercicio que se simula.
Imagen tomada de un software de simulación.
Conclusiones
 Las funciones trigonométricas son de gran importancia ya que nos ayuda en
la representación de fenómenos aperiódicos. Se las aplica mucho en las
telecomunicaciones.
 Toda función trigonométrica de un ángulo 𝜗 pueden ser construidas
geométricamente en relación a una circunferencia de radio unidad de centro
0.
 La inversa de una función siempre será una función aperiódica.
 Si una función es continua y estrictamente creciente o decreciente en un
intervalo, entonces posee función inversa la cual también es continua y
estrictamente creciente o decreciente.

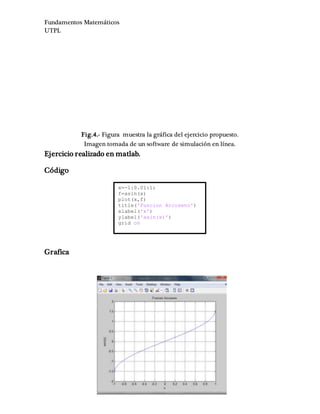
6. Fundamentos Matemáticos
UTPL
Referencias
[1] Concepto de funciones exponenciales [en línea]. Disponible en <
http://es.scribd.com/doc/4607532/FUNCIONES-TRIGONOMETRICAS-
INVERSAS >
[2] Obtención de graficas [en línea]. Disponible en < http://
wolframalpha.com/input/?i=arcsin%28raiz+3%2F2%29>
[3] Obtención de gráficas y simulación [software Matlab].
[4] Obtención de graficas [Geogebra].