Este documento presenta una guía para graficar funciones matemáticas usando el programa Graphmatica. Incluye instrucciones para graficar funciones lineales, familias de funciones, encontrar ceros y pendientes de funciones, y ajustar los rangos de las cuadrículas para visualizar mejor las gráficas. El estudiante debe completar los ejercicios gráficos siguiendo las instrucciones proveídas.

1. Facultad de Educación
Pedagogía Básica Intercultural
Didáctica de Matemática Intercultural
Guía de
Graphmatica
Estudiante:
Maximiliano Sandoval Sandoval
Docente:
Karla Sepúlveda.
Temuco 23 de mayo de 2014

2. Guía de Graphmatica
1) Representar gráficamente las siguientes funciones:
2
1
 xy
y= x+1

3. y=x-2,3
y=x+5
y=x

4. a) ¿Qué ocurre con las gráficas de estas funciones? ¿Qué tienen en
común? ¿En qué se diferencian?
R: lo que ocurre en el grafico es que todas las funciones son lineales
ascendente o descendente según el valor que adopten X e Y en la
función. Lo que tienen en común es que cuatro de las funciones
lineales pasan por un punto de los ejes X e Y. En lo que se diferencian
es que una de las funciones lineales solamente pasa por el punto de
origen.
b) Ajustar el rango de la cuadrícula para que puedan visualizarse todas
las ordenadas de las funciones.
2) Graficar la función axy  . (Aclaración: Observar que a es un parámetro
que cumple las condiciones que aparecen entre llaves de la siguiente manera:
{a: valor inicial, valor final, intervalos})
y= x+a

5. a) Graficar la familia de funciones axy  con 34  a siendo a un
número entero.
3) ¿Qué relación existe entre la ordenada de una función lineal y su
representación gráfica?
R: La relación que existe entre la ordenada de una función lineal, es que
casi la mayoría de la veces la función lineal intercepta o atraviesa a la
ordenada en uno de sus puntos. Representándose en la grafica como una
recta ascendente o descendente.
4) Graficar las siguientes familias de funciones de la forma xay  (copiar
el gráfico y pegarlo en cada actividad):
y=x+2

6. a) 31  a siendo a un número entero. xy  2
b) 15  a siendo a un número entero. xy  3
c) ¿Qué relación existe entre la pendiente de una función lineal y su
representación gráfica?
La pendiente de la función lineal depende del valor que adopte la letra
a, ya que si su valor en positivo la gráfica de la pendiente de la
función lineal es:

7. Mientras que si el valor de a es negativo la pendiente está mirando
para el otro lado, es decir para el lado inverso de la función lineal con
a positivo:
5) Graficar una función lineal creciente con ordenada al origen negativa y no
entera. Con la ayuda del graficador, responder:
a) Encontrar el cero de la función.
Y=-x+0

8. R: El cero se encuentra en el origen de la función lineal como se observa en
la imagen de la función y=-x+0
b) Establecer el valor para  4,0f
c) ¿Para qué valor de x se obtiene   3xf ?
d) Limpiar la pantalla, fije el dominio de la función en el intervalo  2;3 .
y= -1*3+6

9. 6) Dibujar la función 12
 xy en las siguientes pantallas. Copiar cada
gráfico y pegarlo en este mismo archivo:
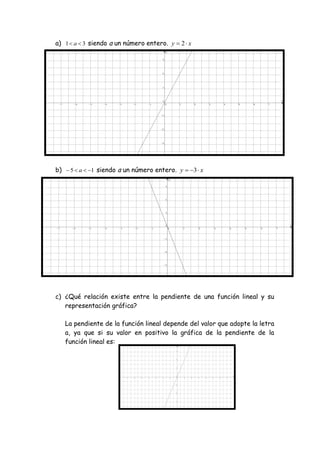
a) [-2, 2] por [-2, 2]
b) [-10, 10] por [-5, 30]
12
 xy

10. c) [-2, 4] por [-4, 4]
d) [-50, -20] por [-100, 100]
e) [-50, 50] por [-100, 1000]

11. f) ¿Qué conclusiones se pueden extraer? Determinar cuál de las
pantallas produce la gráfica más apropiada.
R: Todas las graficas están correctamente graficadas, ya que todos
los puntos dados calzan con el eje X y el eje Y tal cual como se pide.
Es por ello que todas las graficas están buenas según los grafica que
generaban.