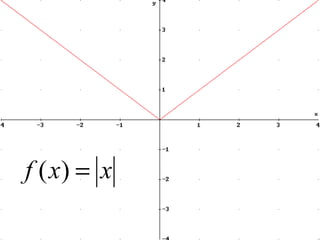
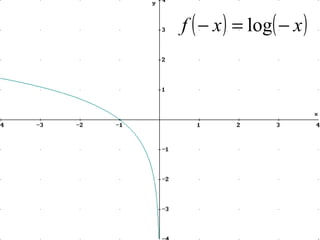
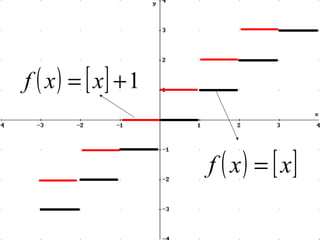
El documento define y explica los conceptos básicos de las funciones, incluyendo su definición, representación gráfica, dominio, recorrido, funciones de primer grado, funciones cuadráticas, funciones logarítmicas y exponenciales, análisis del vértice y discriminante de funciones cuadráticas, y traslaciones y reflexiones de funciones con respecto a los ejes x e y.

1. FUNCIONES

2. Contenidos: Definición Análisis de Función: De primer grado Valor Absoluto Parte Entera Exponencial Logarítmica Cuadrática Función Raíz

3. Definición: Relación entre dos conjuntos, uno de partida denominado Dominio y uno de llegada denominado Recorrido.

4. Se denomina “X imagen de A” ó “A pre imagen de X”

5. Representación cartesiana

6. Condiciones: Para que una relación cualquiera se defina como función nunca puede ocurrir que: Un elemento del dominio tenga dos imágenes en el recorrido. Algún elemento del Dominio no tenga imagen.

11. Evaluación de funciones

12. Función algebraica 1 2 3 4 3 5 7 9

14. Función Creciente

15. Función Decreciente

16. Función Par

17. Función Impar

18. Función de primer grado Función Afín Función Lineal Función constante

19. Función de primer grado Exponente de la variable igual a 1. Tiene como representación gráfica una recta. Dom f: IR Rec f: IR

20. Función Lineal Función de Primer grado con coeficiente de posición igual a cero que por ende pasa por el origen del plano cartesiano

22. Caso particular de la función lineal Función identidad

23. Función Afín Función de primer grado con coeficiente de posición distinto de cero, que por ende no pasa por el origen del sistema cartesiano

25. Función constante Función que no depende de la variable x, y que por ende es representada en el plano cartesiano como una recta paralela al eje x

27. Función parte entera Define la imagen de cada elemento del dominio como el mayor valor entero menor o igual al número

30. Función Valor Absoluto Define la imagen de todos los valores como números positivos.

32. Vértice

34. Función raíz cuadrada

36. Función Exponencial Exponente Variable Base Constante

37. Función Creciente Función decreciente

38. Asíntota en eje x Asíntota en eje x Asíntota en eje x

40. Función logarítmica

41. Función Creciente Función decreciente

42. Asíntota eje y

43. Función cuadrática Exponente mayor de la variable igual a 2. Su gráfica esta representada por una parábola.

44. Vértice

45. Eje de simetría Valor mínimo

46. Intersecciones con el eje x Dada una ecuación cuadrática que se puede factorizar de la forma ; Las soluciones de dicha ecuación que representan las intersecciones con el eje x serán

47. Fórmula cuadrática Dada una ecuación cuadrática de la forma Si tiene intersecciones con el eje x estas se pueden calcular utilizando la fórmula cuadrática

49. CUADRÁTICAS INCOMPLETAS

52. FORMA CANÓNICA DE LA FUNCIÓN CUADRÁTICA

54. Análisis de discriminante Se define el discriminante de la forma:

58. Traslación y reflexión de funciones

59. Traslación en el eje x Dada una función f(x), trasladarla “a” unidades hacia la derecha se representa como f(x-a) Trasladarla a unidades hacia la izquierda se representa como f(x+a)

60. Ejemplos

61. Dada la función Trasladarla 3 unidades hacia la derecha se representa de la forma

64. Dada la función Trasladarla 2 unidades hacia La izquierda se representa de La forma

67. Traslación en el eje y Dada una función f(x), trasladarla “a” unidades hacia arriba (en el eje y) se representa de la forma f(x)+a. Trasladarla “a” unidades hacia abajo se representa de la forma f(x)-a

68. Ejemplos

69. Dada la función exponencial de la forma Trasladarla 2 unidades hacia Arriba se representa de la forma

72. Dada la función valor absoluto de la forma Trasladarla 2 unidades hacia Abajo se representa de la forma

75. Reflexión en el eje x Dada una función f(x), la representación simétrica (refelxión) en torno el eje x se representa de la forma –f(x)

76. Dada la función cuadrática De la forma La reflexión en torno al eje x Se representa como

79. Reflexión en el eje y Dada una función f(x), la representación simétrica (refelxión) en torno el eje y se representa de la forma f(-x)

80. Dada la función logarítmica De la forma La reflexión en torno al eje y Se representa como

83. Reflexión de una función cuadrática con respecto al eje x

87. Casos Particulares

89. Trasladarla una unidad hacia arriba

91. Para toda función de primer grado con pendiente igual a 1

93. Al desplazarla una unidad hacia arriba

95. Para toda función

96. Funciones Traslación Reflexión Eje x Eje y Eje x Eje y Se suma o resta a la variable f(x+a) Se suma o resta a la función f(x)+a Inverso aditivo de la función -f(x) Inverso aditivo de la variable f(-x)