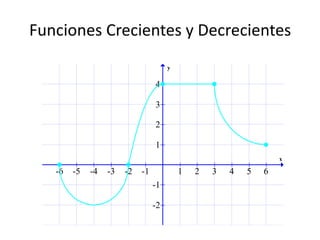
Este documento presenta los conceptos fundamentales de gráficas de funciones en precálculo. Explica cómo identificar funciones pares e impares a partir de una gráfica o ecuación, y cómo determinar si una función es creciente, decreciente o constante utilizando una gráfica. También cubre cómo usar una gráfica para localizar máximos y mínimos locales de una función, y cómo calcular la razón de cambio promedio.

1. Tema IIIGráficas de FuncionesPrecálculo

2. ObjetivosDeterminar funciones pares e impares de una gráfica.Identificar funciones pares e impares de una ecuación.Utilizar una gráfica para determinar cuando una función es creciente, decreciente o constante.Utilizar una gráfica para localizar máximos y mínimos locales.Encontrar la razón de cambio promedio de una función.

3. Funciones Pares e ImparesUna función f es par si para cada número x en su dominio el número –x también está en su dominio y f(-x) = f(x).Una función f es impar si para cada número x en su dominio el número –x también está en su dominio y f(-x) = -f(x).TeoremaUna función es par si y solamente si es simétrica con respecto al eje de y. Una función es impar si y solamente si es simétrica con respecto a origen.

4. Determinando Funciones Pares e Impares de una GráficaDetermina cual de las siguientes gráficas representa una función par, impar o ninguna.

5. Identificando Funciones Pares e ImparesClasifica las siguientes funciones en par, impar o ninguna. Luego establece si es simétrica con respecto a el eje de y o con respecto al origen.

6. Funciones Crecientes y Decrecientes

7. Funciones Crecientes o Decrecientes

8. Máximos Locales; Mínimos Locales

9. Encontrando Máximos y Mínimos Locales de la Gráfica de una Función¿En qué número(s), si alguno, f tiene un máximo local?¿Cuál es el máximo local?¿En qué número(s), si alguno, f tiene un mínimo local?¿Cuál es el mínimo local?¿Para cuáles intervalos la función f es creciente y para cuáles es decreciente?

10. Razón de Cambio Promedio

11. Encontrando la Razón de Cambio Promedio