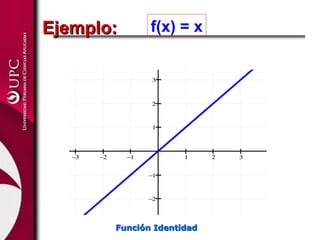
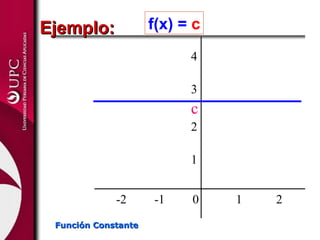
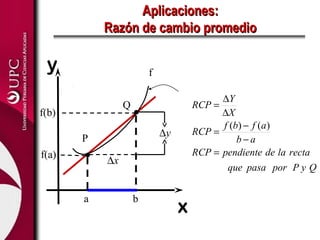
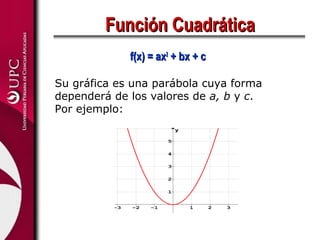
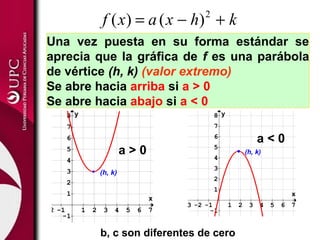
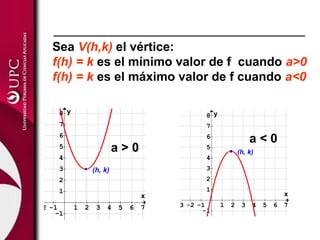
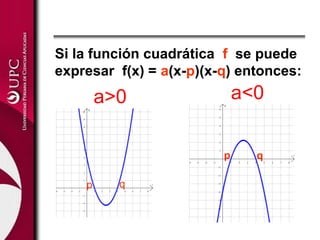
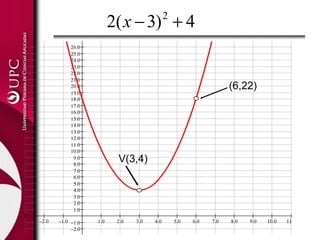
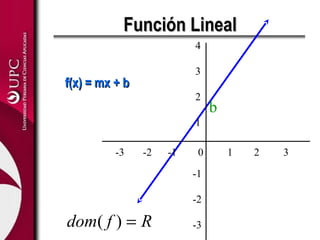
Este documento presenta las funciones lineal y cuadrática. Explica que la función lineal se define por la ecuación f(x)=mx+b, donde m es la pendiente y b es la ordenada en el origen. La función cuadrática se define por f(x)=ax2+bx+c, donde su gráfica es una parábola. El documento analiza las aplicaciones de ambas funciones y cómo identificar sus elementos clave, como el vértice de una función cuadrática.

1. Matemática Básica para
Economistas MA99
UNIDAD 6
Clase 11.2
Tema: Función Lineal y Función Cuadrática

2. Objetivos:
• Presentar la fórmula general de la función lineal
e identificar sus elementos (pendiente y
ordenada en el origen)
• Presentar la fórmula general de la función
cuadrática e identificar sus elementos (vértice)
• Estudiar las aplicaciones de la función lineal y
cuadrática.

3. Función Lineal
f(x) = mx + b
m es la pendiente de la ecuación de la recta
b es la ordenada en el origen
Cuando m = 0, la función se denomina
“función constante”
f(x) = b

4. Función Lineal
4
3
f(x) = mx + b
2
b
1
-3 -2 -1 0 1 2 3
-1
-2
dom( f ) = R -3

5. Ejemplo: f ( x) = x + 3 ; x ∈ [ − 1, 2]
5
4
3
2
1
−4 −3 −2 −1 1 2 3 4 5 6

6. Ejemplo: f(x) = x
5
4
3
2
1
−5 −4 −3 −2 −1 1 2 3 4 5
−1
−2
−3
Función Identidad

7. Ejemplo: f(x) = c
4
3
c
2
1
-2 -1 0 1 2
Función Constante

8. Función Lineal: Aplicaciones
1. Los costos variables y fijos de producción de cierto artículo
son $30 y $24,000, respectivamente. Si el precio es de $40,
determine y grafique en un mismo sistema de coordenadas
las funciones de costo e ingreso. Determine el punto de
equilibrio y grafique la utilidad.
2. Dadas las funciones de oferta: p – q =10 y de demanda:
2p + q = 80. Si la gráfica de la función de oferta se traslada
en forma paralela de tal manera que el nuevo precio de
equilibrio es 28. Hallar la nueva ecuación de la oferta y la
cantidad de equilibrio correspondiente. Grafique.

9. Función Lineal: Aplicaciones
3. Un consumidor gasta siempre todo su ingreso (I) en la
compra de dos tipos de bienes (x,y) cuyos precios unitarios
son Px y Py.
a) Hallar y graficar una ecuación que represente todas las
combinaciones posibles de cantidades que se pueden
adquirir de cada bien.
b) ¿Cómo se traslada la gráfica si:
 Px se triplica?
 Px se reduce a la mitad?
 I se duplica?
 Ambos precios se duplican?

10. Aplicaciones:
Razón de cambio promedio
y f
∆Y
Q RCP =
f(b) ∆X
f (b) − f (a )
∆y RCP =
P b−a
f(a) RCP = pendiente de la recta
∆x
que pasa por P y Q
a b
x

11. Aplicaciones:
Razón de cambio promedio
La siguiente tabla muestra las ventas en dos años
diferentes en dos tiendas en una cadena de
tiendas de descuento.
Tienda Ventas en Ventas en
1992 1995
A $100 000 $160 000
B $50 000 $140 000
Un estudio de los libros de la empresa sugiere que
las ventas de ambas tiendas han crecido
linealmente (es decir, las ventas pueden
aproximarse por una función lineal con bastante
precisión).

12. Aplicaciones:
Razón de cambio promedio
a) Encuentre una ecuación lineal que
describa las ventas de la tienda A
y = 20 000x + 100 000
b) Encuentre una ecuación lineal que describa
las ventas de la tienda B
y = 30 000x + 50 000
c) Encuentre la razón de cambio
promedio en “a”.
$ 60 000
R.C.P en ventas = = $ 20 000 por año
3

13. Aplicaciones:
Razón de cambio promedio
d) Encuentre la razón de cambio promedio
en “b”.
$ 90 000
R.C.P en ventas = = $ 30 000 por año
3
e) Compare resultados
Conclusión:
Si f(x) = mx +b es una función lineal,
entonces la razón de cambio promedio de
y con respecto a x es la pendiente de la recta

14. Costo Marginal
Suponga que el costo de producir radios –
reloj puede aproximarse mediante el
modelo lineal C(x) = 12x + 100
donde C(x) es el costo en dólares por
producir “x” radios- reloj.
a) ¿Cuál es el costo de producir 0 radios-reloj?
b) ¿Cuál es el costo de producir 5 radios- reloj?
c) ¿Cuál es el costo de producir 6 radios- reloj?
d) ¿Cuál es el costo de producir el sexto radio?
e) ¿Cuál es el costo de producir el radio número 81?
f) ¿Cuál es el costo adicional por radio?

15. Función Cuadrática
f(x) = ax2 + bx + c
Su gráfica es una parábola cuya forma
dependerá de los valores de a, b y c.
Por ejemplo:
y
5
4
3
2
1
x
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-1
-2

16. Función Cuadrática
y = ax + bx + c
2
 2
b   2 b 
y −  c −  = a x + 
2
 4a  2a 
  
 2 b 
y = a x + x  + c
y − k = a( x − h )
2
 a 
 2 b  b 2  b 2 Parábola
y = a x + x +   −    + c
 a  2a   2a  
  b b2
h=− k =c−
2 2a 4a
 2 b  b2
y = a x +  + c −
 2a  4a

17. f ( x ) = a ( x − h) + k 2
Una vez puesta en su forma estándar se
aprecia que la gráfica de f es una parábola
de vértice (h, k) (valor extremo)
Se abre hacia arriba si a > 0
Se abre hacia abajo si a < 0
8 y 8 y
7 7
6 6
a<0
5 a>0 5
4
(h, k)
4
3 3
(h, k)
2
2
1
1 x
x
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1
-1
-2
-2
b, c son diferentes de-3
cero

18. Sea V(h,k) el vértice:
f(h) = k es el mínimo valor de f cuando a>0
f(h) = k es el máximo valor de f cuando a<0
8 y 8 y
7 7
6 6
a<0
5 a>0 5
(h, k)
4 4
3 (h, k) 3
2 2
1 1
x x
6 -5 -4 -3 -2 -1 1 2 3 4 5 6-77-6 -5 -4 -3 -2 -1
-1
1 2 3 4 5 6 7
-1
-2
-2
-3
-3

19. Ejemplos:
Para cada función cuadrática
a. Exprese f en forma estándar
b. Trace la gráfica de f
c. Determine el valor extremo de f.
d. Intersecciones con los ejes.
e. Determine el valor de las funciones f y g
para x = -b/2a Analice.
f ( x) = 5 x − 30 x + 49
2
g ( x) = − 2 x + 4 x + 5
2

20. Conclusión:
La gráfica de la función :
f(x) = a x2+ b x + c
tiene su vértice en el punto de
coordenadas:
x= -b/2a ; y = f(-b/2a)
= c - b2/4a

21. Ejemplos:
Para cada función cuadrática
a. Determine el valor extremo de f.
b. Intersecciones con los ejes.
c. Trace la gráfica de f.
g(x) = −2x + 12x − 19
2
h(x) = x −x −6 2

22. Un caso particular
Cuando se traza la gráfica de una
función cuadrática, a la recta vertical
que pasa por el vértice se le denomina
“eje de simetría”
Si la gráfica de una función cuadrática
corta al eje “x” en dos puntos, la
abscisa del vértice es igual a la semi-
suma de las abscisas de estos puntos
de corte.

23. Si la función cuadrática f se puede
expresar f(x) = a(x-p)(x-q) entonces:
a>0 y
a<0
y 6
10
5
9
4
8
7 3
6 2
5
p
1
−18 −17
4
−16 −15 −14 −13 −12 −11 −10 −9 −8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4
q 5 6 7 8
x
3
−1
2
−2
p q
1
x −3
−11 −10 −9 −8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 −4
−1
−5
−2
−6
−3
−7
−4
−5 −8
−6 −9

24. Ejemplo:
Trace la gráfica de las siguientes funciones:
f(x) = 3( x −2)( x −5)
g(x) = 3( − − x )( x −5)
1

25. Otro caso particular
Si tiene como datos al vértice y otro
punto de paso de una parábola, ¿cómo
puede obtener la regla de
correspondencia de la función que tiene
por gráfica a dicha parábola?
En otras palabras, teniendo h y k más
un punto (x,y) por donde pasa la gráfica,
¿podemos obtener la regla de
correspondencia?

26. Ejemplo: Encuentre la regla de correspondencia de una función
cuadrática cuya gráfica tiene el vértice (3;4) y pasa por el punto
(6;,22).
1) Utilizamos a ( x − h) + k2
2) Para obtener a ( x − 3) + 42
3) Por la información dada -pasa por el punto
(6,22)- sabemos que f(6) = 22
4) Por lo tanto: 22 = a (6 − 3) + 4 2
5) De donde: a = 18 = 2
9
6) Finalmente: 2( x − 3) + 4 2

27. 2( x − 3) + 4 2
26.0
25.0
24.0
23.0
22.0
21.0
20.0 (6,22)
19.0
18.0
17.0
16.0
15.0
14.0
13.0
12.0
11.0
10.0
9.0
8.0
V(3,4)
7.0
6.0
5.0
4.0
3.0
2.0
1.0
−2.0 −1.0 −1.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0 11.0
−2.0

28. Función Cuadrática
Aplicaciones
1. Al producir q artículos el costo total está dado por 1,500 +
12q dólares y el precio por p = 40 – q/20 dólares.
Determinar:
a) La función de utilidad y el punto de equilibrio. Graficar.
b) La utilidad máxima.
c) ¿Para qué cantidad de artículos se produce ganancia?
2. Dadas las ecuaciones de oferta: p = q2/20 – q/5 + 16/5 y de
demanda: p = -q2/30 – q/5 +76/5:
a) Graficarlas en un mismo plano.
b) Determine el punto de equilibrio.