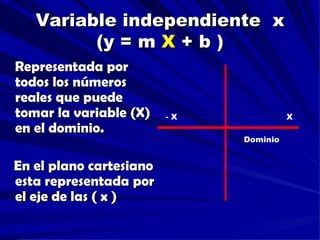
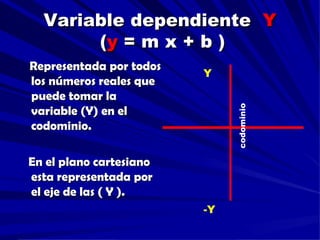
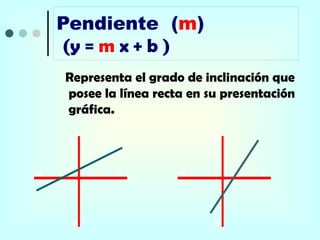
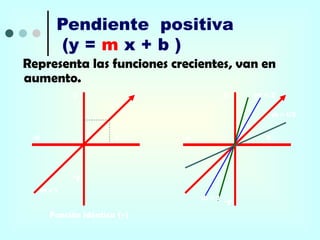
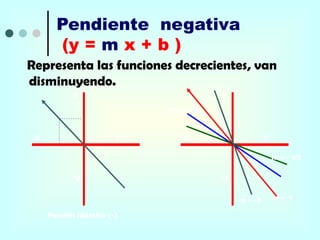
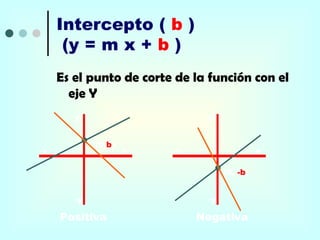
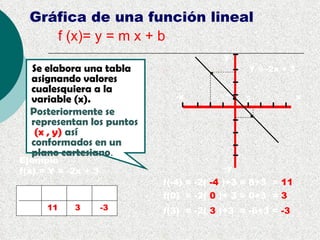
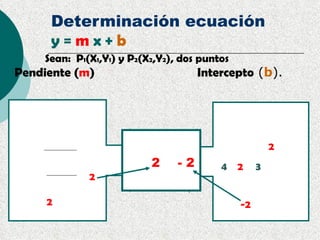
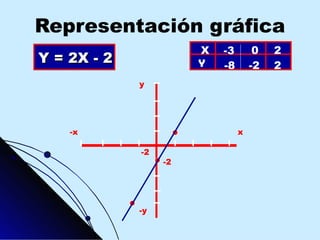
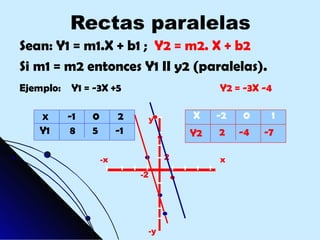
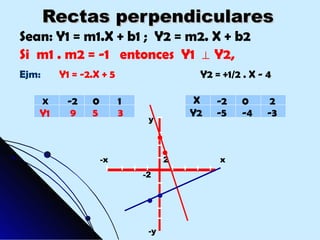
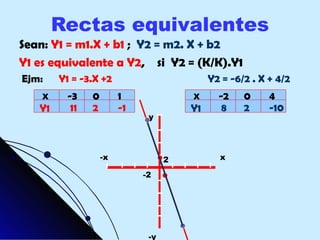
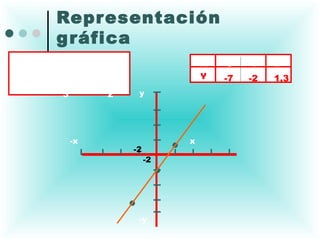
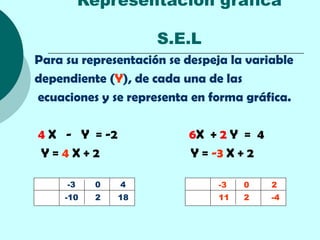
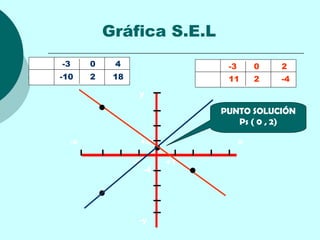
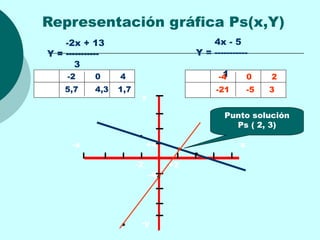
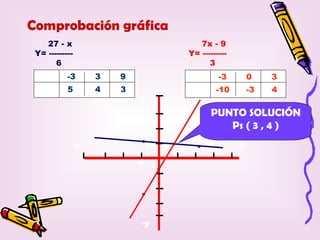
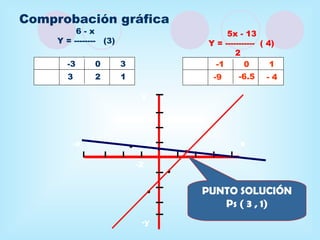
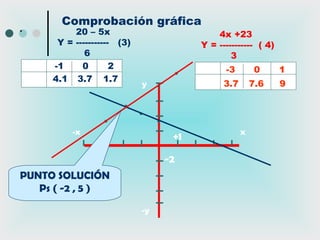
Este documento proporciona una explicación detallada de las funciones lineales, incluyendo la ecuación general de una función lineal (y = mx + b), el significado de las variables independientes y dependientes, la pendiente, el intercepto, cómo graficar una función lineal, cómo determinar la ecuación de una recta a partir de dos puntos, rectas paralelas y perpendiculares, funciones fraccionarias, sistemas de ecuaciones lineales y métodos para resolver sistemas de ecuaciones lineales como igualación, sustitución y determinantes.

1. FUNCIÓN LINEAL

2. FUNCIÓN LINEAL
ECUACIÓN GENERAL
Y = mX+b
Significado:
Y ………. Variable dependiente
X …........ Variable independiente
m ……… pendiente
b ……… intercepto

3. Variable independiente x
(y = m X + b )
Representada por
todos los números
reales que puede
tomar la variable (X) -X X
en el dominio.
Dominio
En el plano cartesiano
esta representada por
el eje de las ( x )

4. Variable dependiente Y
(y = m x + b )
Representada por todos
Y
los números reales que
puede tomar la
codominio
variable (Y) en el
codominio.
En el plano cartesiano
esta representada por
el eje de las ( Y ).
-Y

5. Pendiente (m)
(y = m x + b )
Representa el grado de inclinación que
posee la línea recta en su presentación
gráfica.
y y
-x x -x x
-y -y

6. Pendiente positiva
(y = m x + b )
Representa las funciones crecientes, van en
aumento.
y y m=2
m = 1/2
-x x -x x
-y
m=1
m = 3 -y
Función idéntica (+)

7. Pendiente negativa
(y = m x + b )
Representa las funciones decrecientes, van
disminuyendo.
y y
m = - 1/2
-x x -x x
m = - 1/3
-y -y
m = -3 m = -1
Función idéntica (-)

8. Intercepto ( b )
(y = m x + b )
Es el punto de corte de la función con el
eje Y
y y
(0,b)
-x x -x x
(0, -b)
-y -y
p
Positiva Negativa
o

9. Gráfica de una función lineal
f (x)= y = m x + b
y
Se elabora una tabla Y = -2x + 3
asignando valores
cualesquiera a la 4
variable (x). -x 2 x
Posteriormente se
representan los puntos
(x , y) así
conformados en un
plano cartesiano.
Ejemplo
f(x) = Y = -2x + 3 -y
f(-4) = -2( -4 )+3 = 8+3 = 11
(x) -4 0 3 f(0) = -2( 0 )+ 3 = 0+3 = 3
f (x) 11 3 -3 f(3) = -2( 3 )+3 = -6+3 = -3

10. Determinación ecuación
y=mx+b
Sean: P1(X1,Y1) y P2(X2,Y2), dos puntos
Pendiente (m) Intercepto (b).
P1( -2, - 6)
Tomar P2( 3 , 4)
P2( 3 , 4)
Y2 – ( Y1 ) Como: Y = 2. X + b
m = X2 – ( X 1 )
4–(-6)
Y=2X-2 4 = 2. ( 3 ) + b
m= 3–(-2)= 2
b = 4 – (2 . 3)
Y = 2. X + b b = -2

11. Representación gráfica
X -3 0 2
Y = 2X - 2 Y -8 -2 2
y
-x x
-2
-2
-y

12. Rectas paralelas
Sean: Y1 = m1.X + b1 ; Y2 = m2. X + b2
Si m1 = m2 entonces Y1 II y2 (paralelas).
Ejemplo: Y1 = -3X +5 Y2 = -3X -4
X -1 0 2 y X -2 0 1
Y1 8 5 -1 Y2 2 -4 -7
-x 2 x
-2
-y

13. Rectas perpendiculares
Sean: Y1 = m1.X + b1 ; Y2 = m2. X + b2
Si m1 . m2 = -1 entonces Y1 ⊥ Y2,
Ejm: Y1 = -2.X + 5 Y2 = +1/2 . X - 4
X -2 0 1 X -2 0 2
Y1 9 5 3 Y2 -5 -4 -3
y
-x 2 x
-2
-y

14. Rectas equivalentes
Sean: Y1 = m1.X + b1 ; Y2 = m2. X + b2
Y1 es equivalente a Y2, si Y2 = (K/K).Y1
Ejm: Y1 = -3.X +2 Y2 = -6/2 . X + 4/2
X -3 0 1 X -2 0 4
Y1 11 2 -1 Y1 8 2 -10
y
-x 2 x
-2
-y

15. Funciones fraccionarias
Una función lineal fraccionaria es de la
Forma: f ( X ) = a/b X + c/d
5 4
X -3 0 2 ej: f(x)= X - 2
3
Y -7 -2 1,3
5 4 15 4 -30 - 12 -42
f(-3) = Y= ---- ( -3 ) – ----- = -- -- = = = -7
3 2 6 6
3 2
5 4 4
f(0) = Y= ---- ( 0 ) – ----- = 0 -- =
2
3 2
5 4 10 4
f(2) = Y= ---- ( 2 ) – ----- = + -- =
3 2
3 2

16. Representación
g ráfica
5 4 X -3 0 2
f(X) = Y= ---- ( X ) – ----- Y -7 -2 1,3
3 2 y
-x x
-2
-2
-y

17. Sistema de ecuaciones
lineales S.E.L
Están formadas por un conjunto de números y variables,
de acuerdo a su número determinan su orden 2X2 ; 3X3 …
Orden 2X2 Orden 3X3
a1 X + b1 Y = c1 a1 X + b1 Y + c1 Z = d1
a2 X + b2 Y = c2 a2 X + b2 Y + c2 Z= d2
a3 X + b3 Y + c3 Z= d3
ejemplo
4 X - Y = -2 9X + 3Y -5Z= 4
-6X + 2 Y = 4 6X - 8Y -3Z= 7
-4 X + 6 Y - 9 Z = -5

18. Representación gráfica
S.E.L
Para su representación se despeja la variable
dependiente (Y), de cada una de las
ecuaciones y se representa en forma gráfica.
4 X - Y = -2 6X + 2 Y = 4
Y=4X+2 Y = -3 X + 2
X -3 0 4 X -3 0 2
Y -10 2 18 Y 11 2 -4

19. Gráfica S.E.L
X -3 0 4 X -3 0 2
. Y -10 2 18
Y 11 2 -4
y
PUNTO SOLUCIÓN
Ps ( 0 , 2)
-x +4 x
-1 +1
-4
-y

20. Punto Solución Ps (x,y)
El punto solución Ps (x , y), es aquel cuyas
coordenadas X, Y al ser reemplazadas en cada
una de las ecuaciones que conforman el sistema
las satisfacen y verifican plenamente. Ejm.
4 X - Y = -2 6X + 2 Y = 4
Ps ( 0 , 2 )
4(0) - (2) = -2 6(0) + 2(2) = 4
0 - 2 = -2 0 + 4 =4
- 2 = -2 4 =4

21. Determinación Ps(x,y) de un sistema de
ecuaciones lineales gráficamente
Sean: 2x + 3y = 13 ; 4x – y = 5 un s.e.l
Despejar la variable (y) de cada ecuación
3y = -2x + 13 -y = - 4x + 5
-2 x + 13 4x-5
Y = --------- Y = --------
3 1
Tabla de valores
X -2 0 4 X -4 0 2
Y 5,7 4,3 1,7 Y -21 -5 3

22. Representación gráfica Ps(x,Y)
-2x + 13 4x - 5
Y = ----------- Y = -----------
3
X -2 0 4 X
1
-4 0 2
Y 5,7 4,3 1,7 Y -21 -5 3
y
Punto solución
Ps ( 2, 3)
-x +4 x
-2 +2
-4
-y

23. Prueba de la solución
Sean: 2x + 3y = 13 4x – y = 5
Ps ( 2 , 3 )
2(2)+3(3) = 13 4(2)-(3)= 5
4 + 9 = 13 8-3=5
13 = 13 5=5
Ps ( 2 , 3 ), es solución del sistema de
ecuaciones lineales:
2x + 3y = 13 (1) ecuación 1
4x – y = 5 (2) ecuación 2

24. Métodos solución S.E.L
La determinación del punto solución Ps(x,y) de un
Sistema de ecuaciones lineales, no siempre Se puede
determinar en forma exacta aplicando el método
gráfico; por esta razón es necesario emplear modelos
analíticos para su determinación. Entre los más
conocidos, Se tienen
Método igualación
Método sustitución
Método reducción
Método determinantes

25. Método igualación
Despejar la misma variable en cada
una de las ecuaciones para
posteriormente igualarlas.
 Se resuelve la ecuación resultante
traspasando las variables a la
izquierda y los números a la derecha.
 Se reemplaza el valor de la variable
obtenido en una de las ecuaciones para
obtener la otra variable.

26. Resolver: x + 6y = 27 (1)
7x - 3y = 9 (2)
1. Despejar de la ecuación (1) , (2) la
variable (Y).
27 – x 7x -9
(3) (4)
Y=------------ Y=------------
6 3
2. Se igualan las expresiones (3) y (4)
27 – x 7x -9
------------ = ------------
6 3
3( 27 – x ) = 6( 7x - 9 )

27. 81 – 3x = 42 x – 54
-3x – 42x = -54 – 81
-45x = - 135
-135
x = ----
-45
x= 3
3. Determinación de la variable (y), reemplazando
x=3, en la ecuación (3)
27 – (3)
24
Y= ------------ = ---- = 4 PUNTO SOLUCIÓN
6
6 Ps ( 3 ; 4 )

28. Comprobación gráfica
27 - x 7x - 9
Y= --------- Y= ---------
6 3
X -3 3 9 X -3 0 3
Y 5 4 3 Y -10 -3 4
y
PUNTO SOLUCIÓN
Ps ( 3 , 4 )
-x +4 x
-4
-y

29. Prueba de la solución
Sistema de ecuaciones: x + 6y = 27 (1)
7x - 3y = 9 (2)
Punto solución: Ps ( 3, 4 )
x + 6y = 27 (1) 7x - 3y = 9 (2)
PUNTO SOLUCIÓN
Ps ( 3 , 4 )
3 + 6(4) = 27 7(3) – 3(4) = 9
3 + 24 = 27 21 – 12 = 9
27 = 27 9=9

30. Método de sustitución
 Despejar una de las variables (X o Y) en
una de las ecuaciones por ejemplo (Y) en
ecuación (1), para posteriormente
sustituirla en la ecuación (2).
 Se resuelve la ecuación resultante
traspasando las variables a la izquierda y
los números a la derecha.
 Se reemplaza el valor de la variable
obtenido en una de las ecuaciones para
obtener la otra variable.

31. x + 3y = 6 (1)
Resolver: 5x – 2y = 13 (2)
1. Despejar de la ecuación (1) la variable (Y)
6-x
Y = -------- (3)
3
2. Sustituir (3) en (2)
6-x
5x – 2 ( -------- ) = 13
3
5x (12-2x)
---- – ---------- = 13
1 3
3(5x) – 1(12-2x)
----------------------- = 13
3
15x – 12 + 2x = 3.13

32. 15x – 12 + 2x = 39
15x + 2x = 39 + 12
17x = 51
x=3
3. Determinación de la variable (y),
reemplazando x=3, en la ecuación (3)
6-x 6–(3) 3
Y = -------- (3) Y = ------------- = ------- = 1
3 3 3
PUNTO SOLUCIÓN
Ps ( 3 ; 1 )

33. Comprobación gráfica
6-x 5x - 13
Y = -------- (3) Y = ----------- ( 4)
2
X -3 3 0 3 X -1 0 1
Y 3 2 1 Y -9 -6.5 -4
y
-x +4 x
-2
PUNTO SOLUCIÓN
Ps ( 3 , 1)
-y

34. Prueba de la solución
Sistema de ecuaciones: x + 3y = 6 (1)
5x - 2y = 13 (2)
Punto solución: Ps ( 3, 1 )
x + 3y = 6 (1) 5x - 2y = 13 (2)
PUNTO SOLUCIÓN
Ps ( 3 , 1 )
(3) + 3(1) = 6 5(3) – 2(1) = 13
3+3=6 15 – 2 = 13
6=6 13 = 13

35. Método reducción
 Determinar la variable que se desea
eliminar por ejemplo, la variable (x).
 Se determina el m.c.m de los coeficientes de
la variable a eliminar en este caso (x).
 Se Igualan los coeficientes de la variable (x),
multiplicando cada ecuación por el
coeficiente adecuado.
 Cambiar todos los signos de una ecuación.
 Sumar miembro a miembro los términos de
las ecuaciones.

36. Resolver la ecuación resultante y
determinar el valor de la variable (y).
 Sustituir dicho valor en la ecuación (1) o (2),
para determinar la otra variable.
 Determinar el punto solución Ps (x,y).
 Comprobar la solución.

37. Resolver: 5x + 6y = 20 (1)
4x – 3y = -23 (2)
 Eliminar (x),
 m.c.m( 5, 4 ) = 20
 (4). (5x + 6y = 20 ) 20x + 24y = 80
(-5). (4x – 3y = -23) -20x + 15y = 115
 Sumar 39y = 195
 Determinar variable Y, Y=5
 5x + 6 (5) = 20 5x = 20 -30
5x = -10 x = -5
 Punto solución: Ps ( -2 , 5 )

38. Prueba de la solución
Sistema de ecuaciones: 5x + 6y = 20 (1)
4x - 3y = -23 (2)
Punto solución: Ps ( -2, 5 )
5x + 6y = 20 (1) 4x - 3y = -23 (2)
PUNTO SOLUCIÓN
Ps ( -2 , 5 )
5(-2) + 6(5) = 20 4(-2) – 3(5) = -23
-10 + 30 = 20 -8 – 15 = -23
20 = 20 -23 = -23

39. Comprobación gráfica
. 20 – 5x 4x +23
Y = ----------- (3) Y = ----------- ( 4)
6 3
X -1 0 2 X -3 0 1
Y 4.1 3.7 1.7
y Y 3.7 7.6 9
-x x
+1
-2
PUNTO SOLUCIÓN
Ps ( -2 , 5 )
-y

40. METODO DE
DETERMINANTES
DEFINICIÓN DETERMINANTE:
Sea: a1 X + b1 Y = c1.
a2 X + b2 Y = c2.
a1 b1
det = W = = a1 . b2 – ( a2 . b1)
a2 b2
W = a1 . b2 – ( a2 . b1)

41. EJEMPLO DE
DETERMINANTES
CALCULO DEL DETERMINANTE:
Sea: 5 X - 8 Y = 6.
-4 X + 3 Y = 2.
5 -8
det = W = = 5 . 3 – ( -4 . (-8))
-4 3
W = 15 – (32)= - 17
W = - 17

42. SOLUCIÓN S.E.L POR DETERMINANTES
Sea: a1 X + b1 Y = c1.
a2 X + b2 Y = c2.
C1 b1 a1 C1
C2 b2 a2 C2
X= Y=
W W
c1 . b2- (c2 . b1) a1 . c2- (a2 . c1)
X= Y=
W W

43. RESOLVER
x + 6y = 27 (1)
7x - 3y = 9 (2)
3. Hallar el determinante del sistema
1 6
Det = w = = 1 . (-3) – ( 7. 6) = - 3 - 42
7 -3
W = -45

44. 2. DETERMINAR EL VALOR DE ( X )
a1 X + b1 Y = c1. x + 6y = 27 (1)
a2 X + b2 Y = c2.
7x - 3y = 9 (2)
C1 b1 27 6
C2 b2 9 -3
X= =
W -45
27 . (-3) – ( 9 . 6 ) -81 - 54 -135
X= = =
-45 -45 -45
X=3

45. 3. DETERMINAR EL VALOR DE ( Y )
a1 X + b1 Y = c1. x + 6y = 27 (1)
a2 X + b2 Y = c2. 7x - 3y = 9 (2)
a1 C1 1 27
a2 C2 7 9
Y= =
W -45
1 . (9) – ( 7 . 27 ) 9 - 189 -180
Y= = =
-45 -45 -45
Y=4

46. 4. Punto solución
Ps ( 3 , 4 )
5. Prueba
• Sistema de ecuaciones: x + 6y = 27 (1)
7x - 3y = 9 (2)
• Punto solución: Ps ( 3, 4 )
x + 6y = 27 (1) 7x - 3y = 9 (2)
3 + 6(4) = 27 7(3) – 3(4) = 9
3 + 24 = 27 21 – 12 = 9
27 = 27 9=9