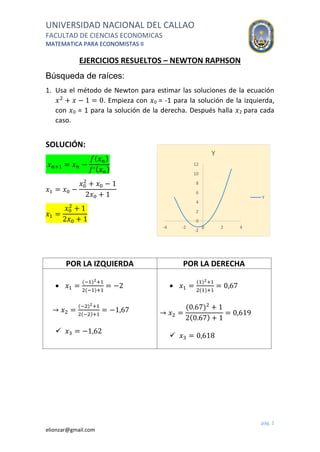
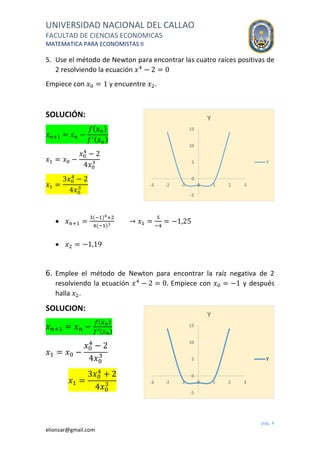
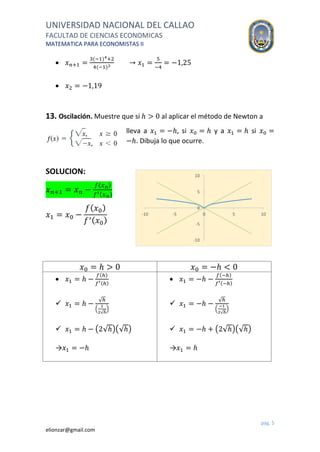
El documento presenta varios ejercicios resueltos utilizando el método de Newton-Raphson para estimar raíces de ecuaciones. Se muestran 6 ejercicios donde se aplica el método para encontrar raíces de ecuaciones cuadráticas, cúbicas y cuárticas, empezando con valores iniciales dados y calculando iteraciones sucesivas hasta aproximar las raíces. El último ejercicio aplica el método para mejorar una estimación inicial de la coordenada de un planeta.

1. UNIVERSIDAD NACIONAL DEL CALLAO
FACULTAD DE CIENCIAS ECONOMICAS
MATEMATICA PARA ECONOMISTAS II
pág. 1
elionzar@gmail.com
EJERCICIOS RESUELTOS – NEWTON RAPHSON
Búsqueda de raíces:
1. Usa el método de Newton para estimar las soluciones de la ecuación
𝑥2
+ 𝑥 − 1 = 0. Empieza con 𝑥0 = -1 para la solución de la izquierda,
con 𝑥0 = 1 para la solución de la derecha. Después halla 𝑥2 para cada
caso.
SOLUCIÓN:
𝑥 𝑛+1 = 𝑥 𝑛 −
𝑓( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
𝑥1 = 𝑥0 −
𝑥0
2
+ 𝑥0 − 1
2𝑥0 + 1
𝑥1 =
𝑥0
2
+ 1
2𝑥0 + 1
POR LA IZQUIERDA POR LA DERECHA
 𝑥1 =
(−1)2+1
2(−1)+1
= −2
→ 𝑥2 =
(−2)2+1
2(−2)+1
= −1,67
 𝑥3 = −1,62
 𝑥1 =
(1)2+1
2(1)+1
= 0,67
→ 𝑥2 =
(0.67)2
+ 1
2(0.67) + 1
= 0,619
 𝑥3 = 0,618
-2
0
2
4
6
8
10
12
-4 -2 0 2 4
Y
Y

2. UNIVERSIDAD NACIONAL DEL CALLAO
FACULTAD DE CIENCIAS ECONOMICAS
MATEMATICA PARA ECONOMISTAS II
pág. 2
elionzar@gmail.com
2. Use el método de newton para estimar una solución real de la ecuación
x3
+3x+1 empieza x0 = 0 y después hallar x2.
SOLUCIÓN:
𝑥 𝑛+1 = 𝑥 𝑛 −
𝑓( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
𝑥1 = 𝑥0 −
𝑥0
3
+ 3𝑥0 + 1
3𝑥0
2
+ 3
𝑥1 =
2𝑥0
3
− 1
3𝑥0
2
+ 3
𝑥1 =
2(0)3
− 1
3(0)2 + 3
= −0.33
𝑥2 =
2(−0,33)3
− 1
3(−0,33)2 + 3
= −0.32
3. Emplee el método de Newton para estimar los dos ceros de la función
𝑓( 𝑥) = 𝑥4
+ 𝑥 − 3. Empiece con x0 = -1 para la solución de la
izquierda, y con x0 = 1 para la solución de la derecha. Después, halle x2
para cada caso.
SOLUCION:
𝑥 𝑛+1 = 𝑥 𝑛 −
𝑓( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
𝑥1 = 𝑥0 −
𝑥0
4+𝑥0−3
4𝑥0
3+1
𝑥1 =
3𝑥0
4
+ 3
4𝑥0
3
+ 1
-10
-5
0
5
10
15
20
-3 -2 -1 0 1 2 3
y
y
-15
-10
-5
0
5
10
15
20
-4 -2 0 2 4
Y
Y

3. UNIVERSIDAD NACIONAL DEL CALLAO
FACULTAD DE CIENCIAS ECONOMICAS
MATEMATICA PARA ECONOMISTAS II
pág. 3
elionzar@gmail.com
POR LA IZQUIERDA POR LA DERECHA
 𝑥1 =
3(−1)4+3
4(−1)3+1
= −2
→ 𝑥2 =
3(−2)4
+ 3
4(−2)3 + 1
 𝑥2 = −1,645
 𝑥3 = −1,485
 𝑥1 =
3(1)4+3
4(1)3+1
= 1,2
→ 𝑥2 =
3(1,2)4
+ 3
4(1,2)3 + 1
 𝑥2 = 1,165
 𝑥3 = 1,164
4. Usa el método de newton para estimar los dos ceros de la función
𝑓( 𝑥) = −𝑥2
+ 2𝑥 + 1. Empieza con 𝑥0 = 0 para la solución de la
izquierda, y con 𝑥0 = 2 para la solución de la derecha. Después halla
𝑥2 para cada caso.
SOLUCION:
𝑥 𝑛+1 = 𝑥 𝑛 −
𝑓( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
𝑥1 = 𝑥0 −
−𝑥0
2+2𝑥0+1
−2𝑥0+2
𝑥1 =
𝑥0
2
+ 1
2𝑥0 − 2
POR LA IZQUIERDA POR LA DERECHA
𝑥1 =
(0)2
+ 1
2(0) − 2
= −0,5
𝑥2 =
(−0,5)2
+ 1
2(−0,5) − 2
𝑥2 = −0416
𝑥1 =
(2)2
+ 1
2(2) − 2
= 2,5
𝑥2 =
(2,5)2
+ 1
2(2,5) − 2
𝑥2 = 2,416
-8
-6
-4
-2
0
2
4
-4 -2 0 2 4
Y
Y

4. UNIVERSIDAD NACIONAL DEL CALLAO
FACULTAD DE CIENCIAS ECONOMICAS
MATEMATICA PARA ECONOMISTAS II
pág. 4
elionzar@gmail.com
5. Use el método de Newton para encontrar las cuatro raíces positivas de
2 resolviendo la ecuación 𝑥4
− 2 = 0
Empiece con 𝑥0 = 1 y encuentre 𝑥2.
SOLUCIÓN:
𝑥 𝑛+1 = 𝑥 𝑛 −
𝑓( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
𝑥1 = 𝑥0 −
𝑥0
4
− 2
4𝑥0
3
𝑥1 =
3𝑥0
4
− 2
4𝑥0
3
 𝑥 𝑛+1 =
3(−1)4+2
4(−1)3
→ 𝑥1 =
5
−4
= −1,25
 𝑥2 = −1,19
6. Emplee el método de Newton para encontrar la raíz negativa de 2
resolviendo la ecuación 𝑥4
− 2 = 0. Empiece con 𝑥0 = −1 y después
halla 𝑥2.
SOLUCION:
𝑥 𝑛+1 = 𝑥 𝑛 −
𝑓( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
𝑥1 = 𝑥0 −
𝑥0
4
− 2
4𝑥0
3
𝑥1 =
3𝑥0
4
+ 2
4𝑥0
3
-5
0
5
10
15
-3 -2 -1 0 1 2 3
Y
Y
-5
0
5
10
15
-3 -2 -1 0 1 2 3
Y
Y

5. UNIVERSIDAD NACIONAL DEL CALLAO
FACULTAD DE CIENCIAS ECONOMICAS
MATEMATICA PARA ECONOMISTAS II
pág. 5
elionzar@gmail.com
 𝑥 𝑛+1 =
3(−1)4+2
4(−1)3
→ 𝑥1 =
5
−4
= −1,25
 𝑥2 = −1,19
13. Oscilación. Muestre que si ℎ > 0 al aplicar el método de Newton a
lleva a 𝑥1 = −ℎ, si 𝑥0 = ℎ y a 𝑥1 = ℎ si 𝑥0 =
−ℎ. Dibuja lo que ocurre.
SOLUCION:
𝑥 𝑛+1 = 𝑥 𝑛 −
𝑓( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
𝑥1 = 𝑥0 −
𝑓( 𝑥0)
𝑓′( 𝑥0)
𝑥0 = ℎ > 0 𝑥0 = −ℎ < 0
 𝑥1 = ℎ −
𝑓(ℎ)
𝑓′(ℎ)
 𝑥1 = ℎ −
√ℎ
(
1
2√ℎ
)
 𝑥1 = ℎ − (2√ℎ)(√ℎ)
→𝑥1 = −ℎ
 𝑥1 = −ℎ −
𝑓(−ℎ)
𝑓′(−ℎ)
 𝑥1 = −ℎ −
√ℎ
(
−1
2√ℎ
)
 𝑥1 = −ℎ + (2√ℎ)(√ℎ)
→𝑥1 = ℎ
-10
-5
0
5
10
-10 -5 0 5 10

6. UNIVERSIDAD NACIONAL DEL CALLAO
FACULTAD DE CIENCIAS ECONOMICAS
MATEMATICA PARA ECONOMISTAS II
pág. 6
elionzar@gmail.com
16. Localización de un planeta. Para calcular las coordenadas de un
planeta en el espacio, tenemos que resolver ecuaciones como f (x) = x - 1 -
0.5senx se sugiere que la función tiene una raíz cerca de 𝑥 = 1,5 Use una
aplicación del método de Newton para mejorar esta estimación. Esto es,
empiece con 𝑥0 = 1,5 y 𝑥1. halla (El valor de la raíz con cinco decimales es
1.49870.) Recuerde utilizar radianes.
SOLUCION:
𝑥 𝑛+1 = 𝑥 𝑛 −
𝑓( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
𝑥1 = 𝑥0 −
𝑓( 𝑥0)
𝑓′( 𝑥0)
𝑥1 = 𝑥 −
𝑥 − 1 − 0.5senx
1 − 0.5cosx
𝑥1 = 1,5 −
1,5 − 1 − 0.5sen(1.5)
1 − 0.5cos(1,5)
→ 𝑥1 = 1,49870
BIBLIOGRAFIA:
THOMAS, CALCULO, UNA VARIABLE
 Ejercicios 3,8(Novena edicion)
 Ejercicios 4,7(Undecima edicion)
-6
-4
-2
0
2
4
-4 -2 0 2 4
y
y