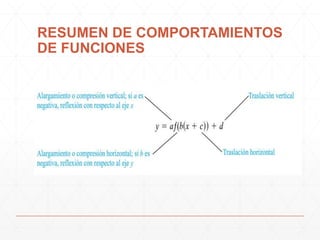
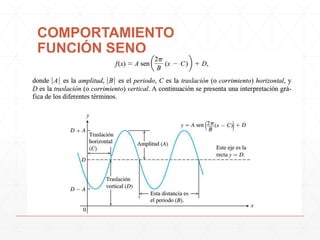
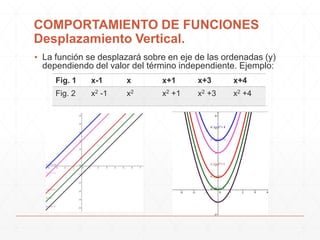
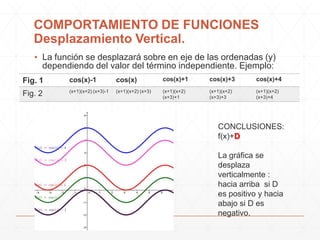
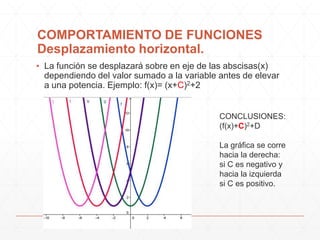
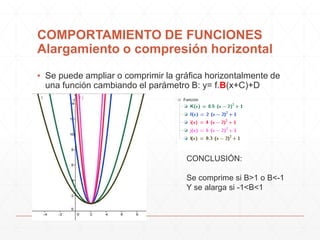
El documento describe diferentes formas en que los parámetros A, B, C y D afectan el comportamiento de las funciones. Cambiar el valor de D produce un desplazamiento vertical de la gráfica, mientras que cambiar C produce un desplazamiento horizontal. Cambiar el valor de B provoca un alargamiento u compresión horizontal de la gráfica, y cambiar A produce un alargamiento o compresión vertical. El documento también muestra cómo modelar el comportamiento de la temperatura a lo largo del día usando la función seno.

1. COMPORTAMIENTO
DE FUNCIONES
CÁLCULO DIFERENCIAL

2. COMPORTAMIENTO DE
FUNCIONES
▪ El comportamiento de la gráfica de una función
y=f(x) se puede modificar cambiando los
parámetros A,B,C o D

3. COMPORTAMIENTO DE FUNCIONES
Desplazamiento Vertical.
▪ La función se desplazará sobre en eje de las ordenadas (y)
dependiendo del valor del término independiente. Ejemplo:
Fig. 1
x-1
x
x+1
x+3
x+4
Fig. 2
x2 -1
x2
x2 +1
x2 +3
x2 +4

4. COMPORTAMIENTO DE FUNCIONES
Desplazamiento Vertical.
▪ La función se desplazará sobre en eje de las ordenadas (y)
dependiendo del valor del término independiente. Ejemplo:
Fig. 1
cos(x)-1
cos(x)
cos(x)+1
cos(x)+3
cos(x)+4
Fig. 2
(x+1)(x+2) (x+3)-1
(x+1)(x+2) (x+3)
(x+1)(x+2)
(x+3)+1
(x+1)(x+2)
(x+3)+3
(x+1)(x+2)
(x+3)+4
CONCLUSIONES:
f(x)+D
La gráfica se
desplaza
verticalmente :
hacia arriba si D
es positivo y hacia
abajo si D es
negativo.

5. COMPORTAMIENTO DE FUNCIONES
Desplazamiento horizontal.
▪ La función se desplazará sobre en eje de las abscisas(x)
dependiendo del valor sumado a la variable antes de elevar
a una potencia. Ejemplo: f(x)= (x+C)2+2
CONCLUSIONES:
(f(x)+C)2+D
La gráfica se corre
hacia la derecha:
si C es negativo y
hacia la izquierda
si C es positivo.

6. COMPORTAMIENTO DE FUNCIONES
Alargamiento o compresión horizontal
▪ Se puede ampliar o comprimir la gráfica horizontalmente de
una función cambiando el parámetro B: y= f.B(x+C)+D
CONCLUSIÓN:
Se comprime si B>1 o B<-1
Y se alarga si -1<B<1

7. COMPORTAMIENTO DE FUNCIONES
Alargamiento o compresión vertical
▪ Se puede ampliar o comprimir la gráfica verticalmente de
una función cambiando el parámetro A: y= A [f.B(x+C)+D]

8. RESUMEN DE COMPORTAMIENTOS
DE FUNCIONES

9. COMPORTAMIENTO
FUNCIÓN SENO

10. Instrucciones para proyecto unidad
▪ Después de registrar la temperatura del día asignado en °C
cada dos horas, realizar una tabla, en la que el dominio (x)
será la hora, y el rango (y) la temperatura en grados.
▪ Encuentra la regla de correspondencia o función, que
aproximadamente cumple con la relación de la temperatura
de tu ciudad.
1. Localizar puntos de coordenadas en Goegebra
2. Insertar cuatro deslizadores: A, B, C y D
3. Graficar la función Seno f(x) = A (sen(B (x + C)) + D)
4. Cambiar valores en deslizadores hasta que los puntos estén
delineados por la gráfica de la función f.