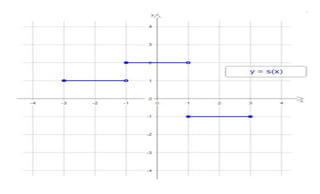
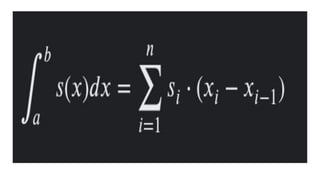La función escalonada se caracteriza por segmentos constantes en su dominio, el cual es un intervalo cerrado, y su rango consiste en los valores de las alturas de los escalones. Es continua salvo en los puntos de cambio, donde su derivada es cero; sin embargo, la derivada no existe en las discontinuidades. La integral de la función corresponde a la suma de las áreas de los rectángulos formados por los escalones.

1. -La función recibe su nombre por la
gráfica en forma de escalones, dados
por los segmentos que la
componen. Cada segmento tiene una
parte del dominio de la función y en
cada uno, la función es constante.

2. -El dominio de una función
escalonada son los valores que
pertenecen al intervalo para el cual
se la define: [a,b], mientras que el
rango lo constituyen los valores si de
las alturas de los escalones.

3. En el ejemplo de la figura 1, el
dominio es el intervalo [-3,3] y el
rango son los valores -1, 1 y 2.

5. -La función escalonada es continua
excepto en los valores que delimitan
cada escalón, los puntos xi.
-Las funciones escalonadas se
pueden sumar y multiplicar para dar
lugar a nuevas funciones
escalonadas.

6. -Su derivada es 0 para los puntos
donde está definida, ya que en ellos
la función es constante. Por su parte,
la derivada no existe en las
discontinuidades.
-La integral de la función escalonada
s(x) entre a y b existe y corresponde

7. a la suma de las áreas de los
rectángulos de anchura xi–xi-1
y altura sk, igual a la del escalón.
Como el área de un rectángulo es el
producto de la base por la altura,
tenemos que: