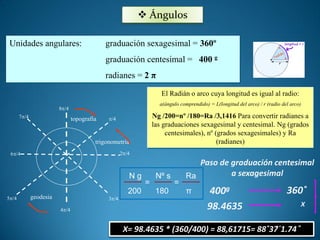
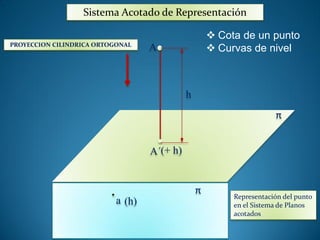
Este documento presenta el programa de una unidad formativa sobre interpretación de mapas y planos topográficos y dibujo de planos sencillos. Incluye el índice general del módulo formativo con las fechas y temas de cada clase, así como índices más detallados de la unidad formativa y de una clase sobre fundamentos de la topografía.

1. Tomás Ramón Herrero Tejedor
Miguel Ángel Conejo Martín
Enrique Pérez Martín
Juan Luis Martín Romero
26 de septiembre al 27 de octubre de 2017
Unidad Formativa 1: Interpretación de mapas y
planos topográficos y dibujo de planos sencillos (30h)
PROGRAMA DE FORMACIÓN PROFESIONAL PARA EL EMPLEO
CERTIFICADO DE PROFESIONALIDAD: Jardinería y restauración del paisaje

2. ÍNDICE GENERAL DEL MÓDULO FORMATIVO - 4
LUNES MARTES MIÉRCOLES JUEVES VIERNES
25/09/17
No lectivo
26/09/17
Fundamentos de la
Topografía (3i)
27/09/17
Fundamentos de la
Topografía (3i)
28/09/17
Interpretación de mapas y
planos topográficos.
Sistemas Digitales (3i)
29/09/17
CAD: Dibujo de planos
(3i)
02/10/17
CAD: Dibujo de planos
(3i)
03/10/17
CAD: Cálculo de superficies
(3i)
1ª Evaluación
04/10/17
Introducción métodos
Práctica 1 (3i)
05/10/17
Introducción métodos
Práctica 2 (3i)
06/10/17
Cálculo y dibujo Práctica 2
Práctica 3 (5i)
09/10/17
Dibujo Práctica 3Ej.
Itinerario cerrado (3i)
10/10/17
Práctica 4 (3i)
11/10/17
Cálculo y dibujo Práctica 4
(3i)
12/10/17
No lectivo
13/10/17
No lectivo
16/10/17
Práctica 5 (3i)
17/10/17
Cálculo y dibujo Práctica 5
(3i)
18/10/17
Práctica 6
Cálculo y dib. Práctica 6 (3i)
19/10/17
Riesgos laborales
2ª Evaluación (3i)
20/10/17
Práctica 7
Cálculo y dib. Práctica 7
(5i)
23/10/17
Fundamentos GNSS (3i)
24/10/17
Práctica 8 Cálculo y dibujo
Práct. 8 (3i)
25/10/17
Práctica 9 (3i)
26/10/17
Práctica 10
3ª Evaluación (3i)
27/10/17
Evaluación Final (5i)

3. ÍNDICE UF-1
U.F. 1: Interpretación de mapas y planos topográficos. Dibujo de planos (30h)
1. Fundamentos de la Topografía
2. Interpretación de Mapas y Planos Topográficos
 Distancias (unidades de medida de longitudes)
 Razones trigonométricas
 Sistema Acotado de Representación
 Sistemas de Coordenadas
 Escalas Cartografía
3. CAD: dibujar, digitalizar, operaciones de cálculo
26/09/2017
27/09/2017
28/09/2017
29/09/2017
02/10/2017
03/10/2017

4. ÍNDICE CLASE
1. Fundamentos de Topografía
 Distancias (unidades de medida de longitudes)
 Distancias
 Pendientes
 Ángulos
 Superficies agrarias
 Conversión de unidades
 Razones trigonométricas
Fundamentos e Introducción a la Topografía
 Sistema Acotado de Representación
Dibujo topográfico: punto, recta, plano, pendiente
 Casos prácticos
descanso

5. Unidades de medida utilizadas en Topografía
 Distancias
 Pendientes
 Ángulos
 Superficies
 Conversión de unidades
1. Fundamentos de Topografía
Topografía: Trata del estudio y aplicación de los métodos e instrumentos
necesarios para llegar a representar el terreno con todos sus detalles,
naturales o no.
La Geodesia es, al mismo tiempo, una de las Ciencias de la Tierra y una Ingeniería.
Trata del levantamiento y de la representación de la forma y de la superficie de
la Tierra, global y parcial, con sus formas naturales y artificiales. (Wikipedia).

6.  Distancias (unidades de medida de longitudes)
Unidades Equivalencia
1 km. (Kilometro) 1.000 m.
1 m. (metro) 10 dm.
1dm. (decimetro) 10 cm.
1cm. (centimetro) 10 mm. (milímetro)
Cadena 10 m
1 Milla náutica
(nudo)
1.863,2 m.
1 Milla estatuaria 1609,3 m.
1 Milla inglés
corriente
(londonmile)
1.523,9 m.
1 Fathom 1,8287 m.
1 Yard 0,9144 m.
1 Pie 0,30448 m.
1 Pulgada 25,399 mm.
Unidades Equivalencia
1 Grado ecuatorial 111,3 km.
1 Grado meridiano 111,12 km.
1 Milla alemana 7,5 km.
1 Nueva Milla
geográfica
7,42 km.
1 Milla marina
alemana
1,852 km.
1 Cable 0,22 km.
1 Braza 1,829 m.
1 Ana prusiana 0,666 m.
1 Vara prusiana 3,766 m.
1 Pie prusiano 0,3139 m.
1 Pulgada
prusiana
2,615 cm

7.  Ángulos
Unidades angulares: graduación sexagesimal = 360º
graduación centesimal = 400 g
radianes = 2 π
topografía
geodesia
trigonometría
8/4
/4
2/4
3/4
4/4
5/4
6/4
7/4
El Radián o arco cuya longitud es igual al radio:
a(ángulo comprendido) = L(longitud del arco) / r (radio del arco)
Ng /200=nº /180=Ra /3,1416 Para convertir radianes a
las graduaciones sexagesimal y centesimal. Ng (grados
centesimales), nº (grados sexagesimales) y Ra
(radianes)
400g
98.4635 X
360˚
X= 98.4635 * (360/400) = 88,61715= 88˚37́´1.74 ̎
Paso de graduación centesimal
a sexagesimal
= =
N g
200 180 π
Nº s Ra

8.  Conversión de unidades
GRADUACIÓN
SEXAGESIMAL
00=3600
900
1800
2700
GRADUACIÓN
CENTESIMAL
100g
200g
300g
RADIANES
/4
0g=400g 8/4=2
7/4
6/4=3/2 2/4=/2
3/45/4
4/4=
3600
89.4568 X
2
X = 89.4568 * ( / 180) = 1,5613 rad
400g
98.4635 Y
2
Y = 98.4635 * ( / 200) = 1,5466 rad
Paso de GRADUACIÓN SEXAGESIMAL
A RADIANES
Paso de GRADUACIÓN CENTESIMAL
A RADIANES

9.  Superficies (unidades de medida)
Unidades Equivalencia
m² 1 m x 1 m
Dm² 100 m²
Hm² 10.000 m²
Mm² 100.000.000 m²
Km² 1.000.000 m²
1 Hectárea 10.000 m2
1 Área 100 m2
1 Centiárea 1 m2
1 Fanega 6.460 m2
1 m². (metro
cuadrado)
100 dm².
1 dm² (decímetro
cuadrado)
100 cm².
1 cm². (centímetro
cuadrado)
100 mm². (milímetro
cuadrado)
Unidades Equivalencia
1 milla cuadrada 2,59 Km2
1 Acre 4046,85 m2
1 Pole cuadrado 25,293 m2
1 Yard cuadrado 0,8361 m2
1 Pie Cuadrado 0,0929 m2
1 Pulgada
cuadrada
6,4516 cm2
1 Milla geográfica
cuadrada
55,0629 km²
1 Yugada prusiana 2.533 m²
1 Vara prusiana
cuadrada
14,0185 m²
1 Peonada bávara 3.407 m²
1 Vara bávara
cuadrada
8,5175 m²
1 Pie cuadrado
prusiano
0,0985 m²

10.  Superficies agrarias
1 Hectárea (Ha) = 10.000 m2
1 Área (a) = 100 m2
1 Centiárea (ca) = 1 m2
Ejemplo: 1.234.567,89 m2 ; 123 - 45 - 67,89 ;
123 Ha 45 a 67.89 ca
123 Ha = 1230000,00 m2
45 a = 4500,00 m2
67,89 ca = 67,89 m2
1.234.567,89 m2

11.  Pasar a hectáreas: 211.943 a
211.943 : 100 = 2 .119,43 ha
 356.500 m2
356.500 : 10 000 = 35,65 hm2 = 35,65 ha
 0,425 km2
0,425 · 100 = 42,5 hm2 = 42,5 ha
 Superficies agrarias

12. Razones trigonométricas
El triángulo rectánguloC
A B
c
b a
90˚
A + B + C = 180˚
a2 = b2 + c2
Seno B =
hipotenusa
lado opuesto
Coseno B =
hipotenusa
lado adyacente
Tangente B =
lado opuesto
lado adyacente
sen B=b/a; cos B=c/a; tgB=b/c
sen C=c/a; cos C=b/a; tgC=c/b

13. Razones trigonométricas
 Seno
 Coseno
 Tangente
Trigonometría: se refiere a la medida de
los lados y los ángulos de un triángulo.
Aplicaciones de la TRIGONOMETRIA:
geodesia, topografía, navegación e
ingeniería.

14. Técnicas Topográficas Aplicadas al Estudio del Mundo Rural

15. Fundamentos e Introducción a la Topografía

16. Distancia Reducida
DEF= g.cos2
DEF = g.sen2
Fundamentos e Introducción a la Topografía

17. Fundamentos e Introducción a la Topografía

18. D= g.sen 
Z= t+i-hp=g.cos  + i -hp
MED
din18723
g
D
hp
t

i
Prisma Reflector

21. Razones trigonométricas
4
3 Utiliza la información de la siguiente figura para contestar
las siguientes preguntas.
Ejercicio:
1. Calcula las seis relaciones trigonométricas para 
75.0
4
3
tangente
8.0
5
4
coseno
6.0
5
3





seno
67.1
3
5
cos ecante
25.1
4
5
sec ante
33.1
3
4
cot angente
5

22. Sistema Acotado de Representación
 Cota de un punto
 Curvas de nivelPROYECCION CILINDRICA ORTOGONAL
π
(+ h)
A
A´
π
(h)a Representación del punto
en el Sistema de Planos
acotados
h

23. Sistema Acotado de Representación
C (4,4,-4)
REPRESENTACION DEL PUNTO: POSICIONES
ZB
A = +3 ZC
B = +4 ZC
A = +7ZB
C = - 4
C´(-4) B´(0)
A´(+3)
9O
Y
X4
4
8
A (4,8,3)
O
Y
Z
X
3
- 4
4 9
8
4 B (9,4,0)

24. π
P
Q
R
A
A´
B , B´
P´, Q´, R´
C
C´
π
B´(0)
C´(- 4)
REPRESENTACION DEL PUNTO: POSICIONES
Sistema Acotado de Representación
P´(+ 5)
Q´(+ 2)
R´ (- 3)
A´(+ 3)

25.  Distancias
27
Definiciones.
Distancia inclinada o geométrica “gA
B ”: Es la distancia recta mas corta que exista entre los puntos dados.
Distancia reducida “DA
B”: Es la longitud del segmento existente entre las proyecciones de los puntos dados.
Desnivel “ZA
B”: Es la diferencia de altura entre los puntos dados y se halla por la diferencia de las cotas de sus
puntos:
Distancia natural “N” entre dos puntos A y B del terreno: Es la distancia formada por la línea sinuosa, resultante
de cortar el terreno natural con un plano vertical que contenga a los puntos A y B.
N
D
ZA
B
A
B
g

26.  Pendientes
A
B
B´(5)
A´(3)
(A)
(B)
π(0)
r
r´
(r)
T(0)

()

ir
ZA
B

Pendiente Pr de la recta r es el valor de la tangente del ángulo : Pr = Tag  = ZA
B / DA
B
ZA
B: Desnivel entre los puntos A y B. DA
B Distancia reducida entre los puntos A y B.
Módulo o intervalo ir es la proyección (o distancia reducida) que existe entre dos puntos de una recta, cuando
su desnivel es la unidad.
Si Z = 1m, la pendiente P y el intervalo i son inversos: P = 1 / i

27. Sistema Acotado de Representación
- Pertenecen a un plano proyectante “a“ y además son perpendiculares entre sí.
Datos:
(ir + is)2 = r2 + s2
h2 = s2 – is
2 ; s2 = h2 + is
2
h2 = r2 – ir
2 ; r2 = h2 + ir
2
ir
2+ is
2 + 2 * ir * is = (h2 + is
2 )+ (h2 + ir
2 )
ir * is = h2
ir * is = h2 ; h = 1 ; ir * is = 1
α = 60º
β = 30ºr´ - s´ (r s)
(s)(r)
(h)
s´- r´α β
ir is
Relación entre rectas perpendiculares:

28. Sistema Acotado de Representación
A
C
B
a c b
d
D
Caso práctico (calcular distancias, cotas y pendientes en tramos rectas) :
1.1 ¿D?
PAB = 17‰
A = 25m
B = 40m
1000m 17m
15mDm
D = 882,353m=
B
Z
A
15m

29. Sistema Acotado de Representación
A
C
B
a c b
d
D
Caso práctico (calcular distancias, cotas y pendientes en tramos rectas) :
1.2 ¿A?
PAB = 15‰
B = 175m
ab = 43cm a E 1/5000
1000 m 15m
215 m
=
B
Z
A
(B-A) =3,225 m
43*5000/1000=215 m
B
Z
A
A= 171,775m

30. Sistema Acotado de Representación
A
C
B
a c b
d
D
Caso práctico (calcular distancias, cotas y pendientes en tramos rectas):
1.3 ¿C?
A = 25m
B = 40m
d = 26 cm
D = 77 cm
E 1/250
C
A
77
26
zA
B
=40-25=15m
77 15
26 Z
Z= 5,06 m
C= 5,06+25=30,06m

31. Sistema Acotado de Representación
A
C
B
a c b
d
D
Caso práctico (calcular distancias, cotas y pendientes en tramos rectas) :
1.4 ¿PAB en %? Si A = 20m
B = 45m
D = 60cm a E:1/1000
P = tg = z A
B
D =
B-A
60*1000/100
=25/600= 0,0416  4,16%

32. Sistema Acotado de Representación
A
C
B
a c b
d
D
Caso práctico (calcular distancias, cotas y pendientes en tramos rectas) :
1.5 ¿i? Si p= tg = Z/D
P=tg  =Z/D = 25/600= 0,0416
iT= 1/P=1/(25/600) =600/25=24 m
P(%)=4,16; iT=1/P=24m; ip=0,024 m =2,4cm
A = 20m
B = 45m
D = 60cm a E:1/1000

33. Sistema Acotado de Representación
A
C
B
a c b
d
D
Caso práctico (calcular distancias, cotas y pendientes en tramos rectas) :
1.6 ¿T0-A´?
A = 20m
B = 45m
D = 600 m a E:1/1000
To(O) A’(2O) B’(45)
A(2O)
B(45)
600m
En 600 m 25 m
20 mTo-A’(x)
T0-A’(x) = 480m
Y en el Dibujo 480/1000 = 0,48 m 48 cm

34.  Curvas de nivel
Sistema Acotado de Representación
30
40
50
60
A H
B
G
C
D
F
Eeq = e = 10 m
A´ B´ C´ D´ E´ F´ G´ H´
Una curva de nivel es aquella línea que en un mapa une todos los puntos que tienen igualdad de
condiciones y de altura. Las curvas de nivel suelen imprimirse en los mapas en color siena para el
terreno y en azul para los glaciares y las profundidades marinas. La impresión del relieve suele
acentuarse dando un sombreado que simule las sombras que produciría el relieve con una
iluminación procedente del Norte o del Noroeste (Wikipedia).

35.  Curvas de nivel
Sistema Acotado de Representación
40
50
60
70
eq

36. Ejercicio: Plano de curvas de nivel
Dibujar el plano a E 1/1000 de los puntos dados con curvas de nivel a
equidistancia 1 m, suponiendo que existe pendiente uniforme en la
dirección de los ejes coordenados (x,y), entre puntos contiguos y de
los puntos 36 y 37 con los 4 mas próximos.
Dibujar las curvas múltiplo de 5 en rojo, el resto en negro.
Nº X Y Z
Nº X Y Z
1 0,00 0,00 23,04
2 40,00 0,00 25,02
3 80,00 0,00 26,22
4 120,00 0,00 22,80
5 160,00 0,00 25,27
6 200,00 0,00 25,51
7 240,00 0,00 22,91
8 0,00 40,00 24,61
9 40,00 40,00 26,90
10 80,00 40,00 26,55
11 120,00 40,00 21,61
12 160,00 40,00 23,94
13 200,00 40,00 23,20
14 240,00 40,00 22,04
15 0,00 80,00 30,22
16 40,00 80,00 29,12
17 80,00 80,00 26,80
18 120,00 80,00 22,22
19 160,00 80,00 24,81
20 200,00 80,00 24,02
21 240,00 80,00 22,80
22 0,00 120,00 31,63
23 40,00 120,00 28,60
24 80,00 120,00 24,93
25 120,00 120,00 23,50
26 160,00 120,00 25,70
27 200,00 120,00 24,66
28 240,00 120,00 22,59
29 0,00 160,00 29,10
30 40,00 160,00 25,11
31 80,00 160,00 23,50
32 120,00 160,00 25,13
33 160,00 160,00 24,66
34 200,00 160,00 23,81
35 240,00 160,00 22,22
36 104,00 145,00 24,95
37 140,00 140,00 24,30

37. 0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240

38. 0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240

39. 0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240
1(23.04) 3(26.22) 4(22.80) 5(25.27) 6(25.51) 7(22.91)2(25.02)
8(24.61) 10(26.55) 11(21.61)
12(23.94) 13(23.20) 14(22.04)9(26.90)
15(30.22)
17(26.80) 18(22.22) 19(24.81) 20(24.02) 21(22.80)16(29.12)
22(31.63)
24(24.93) 25(23.50) 26(25.70) 27(24.66) 28(22.59)23(28.60)
29(29.10) 31(23.50) 32(25.13) 33(24.66) 34(23.81) 35(22.22)30(25.11)
36(24.95)
37(24.30)
Ejercicio: Dibujo de curvas de nivel
En el plano adjunto dibújense las curvas de nivel a equidistancia 1 m, suponiendo que existe pendiente uniforme en la dirección de los ejes coordenados (x,y), entre puntos
contiguos y de los puntos 36 y 37 con los 4 mas próximos.
Apellidos: ………………………………………..… Nombre: …………….………

40. 0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240
1(23.04) 3(26.22) 4(22.80) 5(25.27) 6(25.51) 7(22.91)2(25.02)
8(24.61) 10(26.55) 11(21.61)
12(23.94) 13(23.20) 14(22.04)9(26.90)
15(30.22)
17(26.80) 18(22.22) 19(24.81) 20(24.02) 21(22.80)16(29.12)
22(31.63)
24(24.93) 25(23.50) 26(25.70) 27(24.66) 28(22.59)23(28.60)
29(29.10) 31(23.50) 32(25.13) 33(24.66) 34(23.81) 35(22.22)30(25.11)
36(24.95)
37(24.30)
Ejercicio: Dibujo de curvas de nivel
En el plano adjunto dibújense las curvas de nivel a equidistancia 1 m, suponiendo que existe pendiente uniforme en la dirección de los ejes coordenados (x,y), entre puntos
contiguos y de los puntos 36 y 37 con los 4 mas próximos.
Apellidos: ………………………………………..… Nombre: …………….………

42. 0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240
1(23.04) 3(26.22) 4(22.80) 5(25.27) 6(25.51) 7(22.91)2(25.02)
8(24.61) 10(26.55) 11(21.61)
12(23.94) 13(23.20) 14(22.04)9(26.90)
15(30.22)
17(26.80) 18(22.22) 19(24.81) 20(24.02) 21(22.80)16(29.12)
22(31.63)
24(24.93) 25(23.50) 26(25.70) 27(24.66) 28(22.59)23(28.60)
29(29.10) 31(23.50) 32(25.13) 33(24.66) 34(23.81) 35(22.22)30(25.11)
36(24.95)
37(24.30)
Ejercicio: Dibujo de curvas de nivel
En el plano adjunto dibújense las curvas de nivel a equidistancia 1 m, suponiendo que existe pendiente uniforme en la dirección de los ejes coordenados (x,y), entre puntos
contiguos y de los puntos 36 y 37 con los 4 mas próximos.
Apellidos: ………………………………………..… Nombre: …………….………
31
31
30
30
30
31
30
24
24
25
25
25
26
26
26
26
29
29
29
29
29
29
28
28
28
28
28
28
27
27
27
27
27
27 26
26
26
26
26
26
26
25
25
25
25
25
25
24
24
24
24

43. 0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240
1(23.04) 3(26.22) 4(22.80) 5(25.27) 6(25.51) 7(22.91)2(25.02)
8(24.61) 10(26.55) 11(21.61)
12(23.94) 13(23.20) 14(22.04)9(26.90)
15(30.22)
17(26.80) 18(22.22) 19(24.81) 20(24.02) 21(22.80)16(29.12)
22(31.63)
24(24.93) 25(23.50) 26(25.70) 27(24.66) 28(22.59)23(28.60)
29(29.10) 31(23.50) 32(25.13) 33(24.66) 34(23.81) 35(22.22)30(25.11)
36(24.95)
37(24.30)
Ejercicio: Dibujo de curvas de nivel
En el plano adjunto dibújense las curvas de nivel a equidistancia 1 m, suponiendo que existe pendiente uniforme en la dirección de los ejes coordenados (x,y), entre puntos
contiguos y de los puntos 36 y 37 con los 4 mas próximos.
Apellidos: ………………………………………..… Nombre: …………….………
31
31
30
30
30
31
30
24
24
25
25
25
26
26
26
26
29
29
29
29
29
29
28
28
28
28
28
28
27
27
27
27
27
27 26
26
26
26
26
26
26
25
25
25
25
25
25
24
24
24
24 25
25
24
24
24
25
24
24
25
25
25
25
25
24
24
25
23
2324
2324
25
23 24
23
2324
23
24
24
2322222324
22
2324 23 24 25
24
25
24
25
232425
22