Guia de derivadas en geogebra

UNIVERSIDAD DE CUNDINAMARCA
FACULTAD DE EDUCACION
LICENCIATURA EN MATEMATICAS
ELECTIVA EN EDUCACION MATEMATICA II
TALLERES DE GEOGEBRA
 IDENTIFICACION DEL TALLER
TALLER Nº 02 FECHA 20 de octubre 2014
GRADO: 11 TITULO derivadas en geógebra
UNIDAD:
derivadas
PENSAMIENTOS INCLUIDOS:
Pensamiento métrico y sistemas de medidas
CONOCIMIENTOS PREVIOS:
Al comienzo de esta guía se le recomienda a los estudiantes tener claro algunos
conceptos para su desarrollo, ya que se trabajara con derivadas; conceptos tales
como: definición de derivada, concepto de función, dominio y rango de una
función, inversa de una función, comprender el crecimiento de una función los
máximos y mínimos de la función. Con esto se busca que el estudiante pueda
desarrollar de una manera más fácil y clara la guía.
INTRODUCCION:
Este trabajo busca facilitar el concepto de derivada en los estudiantes de grado
undécimo, de las instituciones donde se aplicara el desarrollo de la guía. Como
el diseño de la guía se realizara en el programa de geógebra el estudiante podrá
analizar el movimiento de las funciones de una forma más dinámica y esto le
ayudara a su razonamiento métrico y lógico y le será de mayor interés por la
parte gráfica y de movimiento.
AUTORES: González Aucique Silvia Liliana
Perdomo Gómez Dany

 COMPONENTES TEORICOS
“La idea central del cálculo diferencial es la noción de derivada al igual que la
integral la derivada fue originada por un problema de geometría; el problema de
hallar la tangente en un punto a una curva”.1
Podemos darnos cuenta que todas las definiciones de matemáticas atreves de
la historia son generadas por un problema al cual se busca dar solución
La definición de la derivada fue solucionada por Isaac Newton y Gottfried
Leibniz estos dos matemáticos desarrollaron los dos siguientes problemas que
se habían planteado con referencia a la derivada como:
 El problema de la tangente a una curva.
 El problema de los máximos y mínimos.
Lo que hoy en día se conoce como calculo diferencia.
Newton y Leibniz desarrollaron parámetros para el uso de la derivada
El uso de derivadas y sus aplicaciones es muy variado;
“las derivadas son útiles en economía, psicología, medicina,
administración, ingeniería, electricidad, electrónica, termodinámica,
mecánica, biología, etc. Se utilizan para la optimización de recursos para
tratar de ocupar el mínimo espacio, tiempo o materiales en algo o
maximizar su espacio; en medicina para obtener un cálculo aproximado
de la velocidad de reproducción de virus, bacterias etc.
En física donde la primera derivada se utiliza para la velocidad y la
segunda para la aceleración. En definitiva las derivadas se suelen usar
para relacionar dos magnitudes”.2
1 Calculus Tom M Apóstol Volumen 1 Editorial Reverte, S.A Pagina 191
2 http://aplicaciones-derivadas.blogspot.com/2009/12/aplicaciones-derivadas-en-la-actualidad.html

Como podemos darnos cuenta la derivada tiene muchas aplicaciones en la vida
cotidiana y soluciona muchos problemas de salud y económicos que se
generan en la actualidad y que son de gran ayuda para las personas.
 METODOLOGIA PARA EL DESARROLLO DE LA GUIA.
Nuestra propuesta de trabajo consiste, en primer lugar, en una guía de trabajos
previos al desarrollo de los contenidos teóricos y prácticos en la interpretación
de la derivada de funciones. Los estudiantes desarrollaran las guías de manera
individual o grupal sin la intervención del docente. El trabajo se corregirá de
manera detallada para que el estudiante fije sus errores y sus aciertos. Todo
esto con un fin, un aprendizaje significativo en la resolución de la derivada y la
interpretación de las graficas, además de una argumentación de las falencias y
como es consecuente su mejoramiento.
Al finalizar cada uno de los trabajos experimentales se reforzara en la temática
consignada en las guías. Ya para terminar se realiza una encuesta como
también una entrevista para cimentar los conocimientos en la temática de
derivada y demás contenidos que se aborden.
 PROCEDIMIENTO PASO A PASO
La propuesta consiste en utilizar el software Geogebra como herramienta para
el aprendizaje del concepto de límite de funciones y se organizó de la siguiente
Manera, Clases con uso de equipos donde se encuentren instalado el
Geogebra, (exploración libre y guía de instrucciones sobre el manejo del
software). Construcción y análisis de funciones en Geogebra, ya que este tema
es necesario para el desarrollo del concepto de derivada
Clase práctica considerando aspectos gráficos y numéricos.

A continuación el estudiante desarrollara la siguiente guie con el fin de aclara el
concepto de derivada.
Ahora hallaremos la derivada de forma gráfica con Geogebra, dada cualquier
función matemática.
1. Abrimos el software Geogebra.
2. En la parte inferior de la pantalla donde se nombra “Entrada”
introducimos la función que queremos graficar en este caso será:

푓(푥) = 푠푒푛2(푥) + 2푥푐표푠(푥).
3. Si damos enter nos debe aparecer una gráfica como la que se muestra
en la siguiente imagen
4. Al obtener la gráfica vamos a la parte superior de la barra de
herramientas y damos clic en la opción de punto y creamos un punto
sobre cualquier parte de la gráfica.

5. Ahora bien vamos al cuarto icono de la barra de herramientas y damos
clic para crear una recta tangente que pasa por el punto y la función.
al dar la opcion de tangente damos clic en el punto A y sobre la funcion

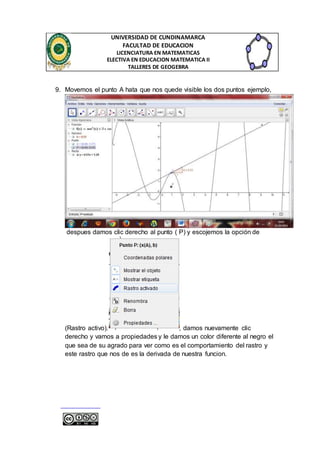
que yatenemos graficada y nos debe dar como resultado lo siguiente.
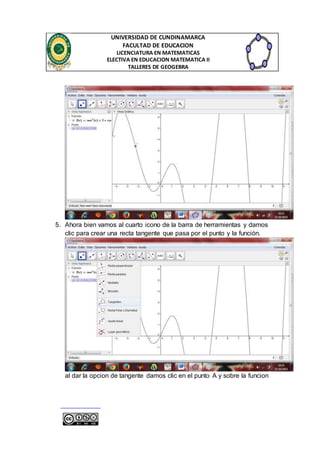
6. Con los pasos anteriores ya desarrollados lo que sigue seria dar clic en
la parte inferior donde dice “Entrada” y escribimos (pendiente) y nos da
como resultado
damos clic en la parte que dice [<Recta>]

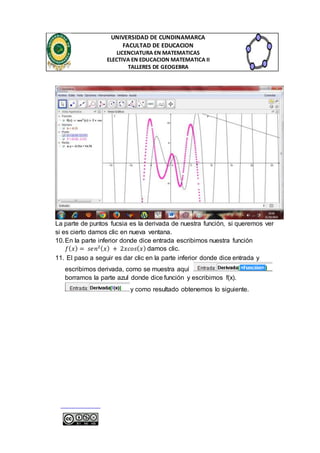
borramos y escribimos la letra a [a] como se muetra en la figura
.
7. Al darle enter debe salir lo siguiente .
para verificar si nos quedo bien nuestra grafica movemos el punto A y
se debe mover la recta y la pendiente.
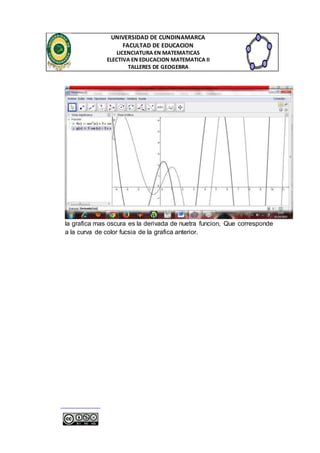
8. Ahora bien despues de verificar si el puto se desplaza por toda la grafica
de nuetra funcion, vamos nuevamente a la aprte inferior en donde dice
entrada y escribimos lo siguinete, que con esto
conseguimos crearun punto P que al mover el punto A tambien se
mueva.

9. Movemos el punto A hata que nos quede visible los dos puntos ejemplo,
despues damos clic derecho al punto ( P) y escojemos la opción de
(Rastro activo). , damos nuevamente clic
derecho y vamos a propiedades y le damos un color diferente al negro el
que sea de su agrado para ver como es el comportamiento del rastro y
este rastro que nos de es la derivada de nuestra funcion.

La parte de puntos fucsia es la derivada de nuestra función, si queremos ver
si es cierto damos clic en nueva ventana.
10. En la parte inferior donde dice entrada escribimos nuestra función
푓(푥) = 푠푒푛2(푥) + 2푥푐표푠(푥) damos clic.
11. El paso a seguir es dar clic en la parte inferior donde dice entrada y
escribimos derivada, como se muestra aquí
borramos la parte azul donde dice función y escribimos f(x).
y como resultado obtenemos lo siguiente.

la grafica mas oscura es la derivada de nuetra funcion, Que corresponde
a la curva de color fucsia de la grafica anterior.

 LISTA DE CHEQUEO
No.
Orden
VARIABLES / INDICADORES DE LOGRO
CUMPLE
Observaciones
SI NO
1.
Justifico resultados obtenidos mediante el
proceso de aproximación sucesiva, rango de
variación derivada en situaciones de medición.
2.
Diseño estrategias para abordar situaciones de
medición que requieran grados de precisión
específico.
3.
Resuelvo y formulo problemas que involucren
magnitudes cuyos valores se suelen definir
indirectamente como razones entre valores de
otras magnitudes.
 4. EVALUACIÓN:
Observaciones:
Recomendaciones:
Juicio de Valor (NOTA):

Guia de derivadas en geogebra

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Guia de derivadas en geogebra

Último

Guia de derivadas en geogebra