Guia de estudio 5 (tema 5 ecuaciones diferenciales ordinarias)

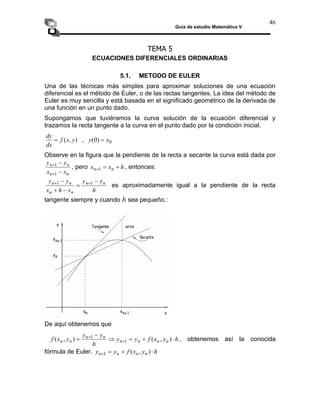
Guía de estudio Matemática V
46
TEMA 5
ECUACIONES DIFERENCIALES ORDINARIAS
5.1. METODO DE EULER
Una de las técnicas más simples para aproximar soluciones de una ecuación
diferencial es el método de Euler, o de las rectas tangentes. La idea del método de
Euler es muy sencilla y está basada en el significado geométrico de la derivada de
una función en un punto dado.
Supongamos que tuviéramos la curva solución de la ecuación diferencial y
trazamos la recta tangente a la curva en el punto dado por la condición inicial.
)
,
( y
x
f
dx
dy
 , 0
)
0
( x
y 
Observe en la figura que la pendiente de la recta a secante la curva está dada por
n
n
n
n
x
x
y
y




1
1
, pero h
x
x n
n 

1 , entonces:
h
y
y
x
h
x
y
y n
n
n
n
n
n 



 
 1
1
es aproximadamente igual a la pendiente de la recta
tangente siempre y cuando h sea pequeño.:
De aquí obtenemos que
h
y
x
f
y
y
h
y
y
y
x
f n
n
n
n
n
n
n
n 




 

)
,
(
)
,
( 1
1
, obtenemos así la conocida
fórmula de Euler. h
y
x
f
y
y n
n
n
n 


 )
,
(
1

47
Con lo cual podemos usar el punto )
,
( 0
0 y
x para construir el siguiente punto
)
,
( 1
1 y
x y así sucesivamente. De esta forma generamos la sucesión de puntos:
)
,
(
,
),
,
(
),
,
( 1
1
0
0 n
n y
x
y
x
y
x 
los cuales es de esperar que se encuentren cercanos a los puntos
))
(
,
(
,
)),
(
,
(
)),
(
,
( 1
1
0
0 n
n x
y
x
x
y
x
x
y
x 
Ejemplo:
Dada la siguiente ecuación diferencial xy
dx
dy
2
 con la condición inicial: 1
)
0
( 
y ,
(a) Resuélvala analíticamente.
(b) Utilice el método de Euler en el intervalo de x = 0 a 1 con tamaño de paso 0.1
(c) Aproxime )
5
.
0
(
y
(d) Grafique y compare los resultados
(a) Solución analítica:
Primero observamos que esta ecuación sí puede resolverse analíticamente (por
métodos tradicionales de ecuaciones diferenciales).
Podemos aplicar el método de separación de variables:
C
x
y
Ln
xdx
y
dy
xdx
y
dy





  
2
2
2
Sustituyendo la condición inicial 1
0 

 y
x
0
0
1 


 C
C
Ln
Por lo tanto, tenemos que la solución está dada:
2
2 x
e
y
x
y
Ln 


(b) Solución Numérica
Aplicamos el método de Euler entre 0 y 1 con tamaño de paso 0.1
Condición inicial: 1
0 

 y
x , )
1
,
0
(
)
,
( 0
0 
y
x
1
.
0
1
.
0
0
0
1 



 h
x
x
1
1
.
0
)
1
)(
0
(
2
1
)
,
( 0
0
0
1 





 h
y
x
f
y
y , )
1
,
1
.
0
(
)
,
( 1
1 
y
x
Aplicando nuevamente la formula de Euler, tenemos, en un segundo paso:
2
.
0
1
.
0
1
.
0
1
2 



 h
x
x

48
02
.
1
1
.
0
)
1
)(
1
.
0
(
2
1
)
,
( 1
1
1
2 





 h
y
x
f
y
y , )
02
.
1
,
2
.
0
(
)
,
( 2
2 
y
x
Resumimos todos los resultados en la siguiente tabla:
iteración xi yi
0 0 1
1 0,1 1
2 0,2 1,02
3 0,3 1,0608
4 0,4 1,124448
5 0,5 1,21440384
6 0,6 1,33584422
7 0,7 1,49614553
8 0,8 1,70560591
9 0,9 1,97850285
10 1 2,33463336
(c) Aproxime )
5
.
0
(
y
De la solución analítica 28403
.
1
)
5
.
0
(
2
)
5
.
0
(

 e
y
De la solución numérica 2144
.
1
)
5
.
0
( 
y
El error relativo porcentual que se cometió al aplicar la formula de Euler esta dado
por:
Er = %
423
.
5
100
28403
.
1
21440
.
1
28403
.
1
100
*






p
p
p
0
0,5
1
1,5
2
2,5
3
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 xi
y
Solución numérica
Solución analítica

49
Aunque la solución numérica aproxima la tendencia de la solución verdadera, el
error aumenta a medida que x aumenta. Es posible reducir el error usando un
tamaño de paso menor.
5.2. METODO DE EULER MODIFICADO
Un motivo fundamental de error en el método de Euler es suponer que la derivada
al inicio del intervalo es la misma durante todo el intervalo. Este método se basa
en la misma idea del método anterior, pero hace un refinamiento en la
aproximación, tomando un promedio entre ciertas pendientes. Esto permite
obtener una mejor aproximación de la pendiente en todo el intervalo.
Las fórmulas son las siguientes:
h
y
x
f
y
y n
n
n
n 


 )
,
(
*
1
h
y
x
f
y
x
f
y
y n
n
n
n
n
n 


 


2
)
,
(
)
,
( *
1
1
1
Para entender esta fórmula, analicemos el primer paso de la aproximación, con
base en la siguiente gráfica:
En la gráfica, vemos que la pendiente promedio m corresponde a la pendiente de
la recta bisectriz de la recta tangente a la curva en el punto de la condición inicial y
la “recta tangente” a la curva en el punto 1
1, y
x , donde 1
y es la aproximación
obtenida con la primera fórmula de Euler. Finalmente, esta recta bisectriz se
traslada paralelamente hasta el punto de la condición inicial, y se considera el
valor de esta recta en el punto 1
x
x  como la aproximación de Euler modificada.
Ejemplo:
dx
dy
2
)
0
( 
y ,

50
(b) Utilice el método de Euler modificado en el intervalo de x = 0 a 1 con tamaño
de paso 0.1
(c) Aproxime )
5
.
0
(
y
Primero observamos que esta ecuación sí puede resolverse analíticamente (por
métodos tradicionales de ecuaciones diferenciales).
Podemos aplicar el método de separación de variables:
C
x
y
Ln
xdx
y
dy
xdx
y
dy





  
2
2
2
Sustituyendo la condición inicial 1
0 

 y
x
0
0
1 


 C
C
Ln
Por lo tanto, tenemos que la solución está dada:
2
2 x
e
y
x
y
Ln 


Aplicamos el método de Euler modificado entre 0 y 1 con tamaño de paso 0.1
Condición inicial: 1
0 

 y
x , )
1
,
0
(
)
,
( 0
0 
y
x
1
.
0
1
.
0
0
0
1 



 h
x
x
1
1
.
0
)
1
)(
0
(
2
1
)
,
( 0
0
0
*
1 





 h
y
x
f
y
y
01
.
1
1
.
0
2
)
1
)(
1
.
0
(
2
0
1
2
)
,
(
)
,
( *
1
1
0
0
0
1 







 h
y
x
f
y
x
f
y
y
)
01
.
1
,
1
.
0
(
)
,
( 1
1 
y
x
Aplicando nuevamente la formula de Euler modificado, tenemos, en un segundo
paso:
2
.
0
1
.
0
1
.
0
1
2 



 h
x
x
0302
.
1
1
.
0
)
01
.
1
)(
1
.
0
(
2
01
.
1
)
,
( 1
1
1
*
2 





 h
y
x
f
y
y
040704
.
1
1
.
0
2
)
0302
.
1
)(
2
.
0
(
2
)
01
.
1
)(
1
.
0
(
2
0
01
.
1
2
)
,
(
)
,
( *
2
2
1
1
1
2 








 h
y
x
f
y
x
f
y
y
)
040704
.
1
,
2
.
0
(
)
,
( 2
2 
y
x

51
iteración xi yi
0 0 1
1 0,1 1,01
2 0,2 1,040704
3 0,3 1,093988045
4 0,4 1,173192779
5 0,5 1,2834729
6 0,6 1,432355757
7 0,7 1,630593794
8 0,8 1,893445513
9 0,9 2,242596866
10 1 2,709057014
(c) Aproxime )
5
.
0
(
y
.
1
)
5
.
0
(
2
)
5
.
0
(

 e
y
.
1
)
5
.
0
( 
y
El error relativo porcentual que se cometió al aplicar la formula de Euler
modificado esta dado por:
Er = %
044
.
0
100
28403
.
1
28347
.
1
28403
.
1
100
*






p
p
p
0
0,5
1
1,5
2
2,5
3
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 xi
y
Solución numérica

52
Vemos que efectivamente se ha obtenido una mejor aproximación con este
método, reduciendo el error relativo verdadero de un 5.423% hasta un 0.044%.
5.3. METODO DE RUNGE - KUTTA
Los Runge-Kutta no es solo un método sino una importante familia de métodos
iterativos tanto implícitos como explícitios para aproximar las soluciones de
ecuaciones diferenciales ordinarias (E.D.O´s), estas técnicas fueron desarrolladas
alrededor de 1900 por los matematicos alemanes Carl David Tolmé Runge y
Martin Wilhelm Kutta.
El clásico método Runge-Kutta de cuarto orden:
Un miembro de la familia de los métodos Runge-Kutta es usado tan comúnmente
que a menudo es referenciado como “RK4” o como “el método Runge-Kutta”.
Definamos un problema de valor inicial como:
0
0 )
(
),
,
( y
x
y
y
x
f
dy
dx


Entonces el método RK4 para este problema esta dado por la siguiente ecuación:
)
2
2
(
6
4
3
2
1
1 k
k
k
k
h
y
y n
n 




 , donde:
)
,
(
1 n
n y
x
f
k 








 1
2
2
,
2
k
h
y
h
x
f
k n
n








 2
3
2
,
2
k
h
y
h
x
f
k n
n
)
,
( 3
4 hk
y
h
x
f
k n
n 


Así, el siguiente valor (yn+1) es determinado por el presente valor (yn) mas el
producto del tamaño del intervalo (h) por una pendiente estimada. La pendiente es
un promedio ponderado de pendientes:
k1 es la pendiente al principio del intervalo;
k2 es la pendiente en el punto medio del intervalo, usando k1 para determinar el
valor de y en el punto xn + h/2 usando el método de Euler
k3 es otra vez la pendiente del punto medio, pero ahora usando k2 para
determinar el valor de y
k4 es la pendiente al final del intervalo, con el valor de y determinado por k3

53
Promediando las cuatro pendientes, se le asigna mayor peso a las pendientes en
el punto medio:
6
2
2 4
3
2
1 k
k
k
k
Pendiente




El método RK4 es un método de cuarto orden lo cual significa que el error por
paso es del orden de h5 , mientras que el error total acumulado tiene el orden h4
Ejemplo:
dx
dy
2
)
0
( 
y ,
(b) Utilice el método de Runge-Kutta de cuarto orden en el intervalo de x = 0 a 1
con tamaño de paso 0.1
(c) Aproxime )
5
.
0
(
y
La solución se obtuvo en el ejemplo anterior fue:
xy
dx
dy
2

2
x
e
y 

Aplicamos el método de Runge-Kutta de cuarto orden entre 0 y 1 con tamaño de
paso 0.1
Condición inicial:
1
0 

 y
x , )
1
,
0
(
)
,
( 0
0 
y
x
1
.
0
1
.
0
0
0
1 



 h
x
x
Aplicamos las ecuaciones del método:
Para xy
y
x
f 2
)
,
( 
0
)
1
)(
0
(
2
)
1
,
0
(
)
,
( 0
0
1 


 f
y
x
f
k
1
.
0
)
1
)(
05
.
0
(
2
)
1
,
05
.
0
(
0
2
1
.
0
1
,
2
1
.
0
0
2
,
2
1
0
0
2




















 f
f
k
h
y
h
x
f
k

54
1005
.
0
)
005
.
1
)(
05
.
0
(
2
)
005
.
1
,
05
.
0
(
1
.
0
2
1
.
0
1
,
2
1
.
0
0
2
,
2
2
0
0
3




















 f
f
k
h
y
h
x
f
k
20201
.
0
)
01005
.
1
)(
1
.
0
(
2
)
01005
.
1
,
1
.
0
(
)
1005
.
0
1
.
0
1
,
1
.
0
0
(
)
,
( 3
0
0
4









 f
f
hk
y
h
x
f
k
0100502
.
1
)
20201
.
0
)
1005
.
0
(
2
)
1
.
0
(
2
0
(
6
1
)
2
2
(
6
1
4
3
2
1
0
1 










h
k
k
k
k
h
y
y
i xi k1 k2 k3 k4 yi yanalitica
0 0 1 1
1 0,1 0 0,1 0,1005 0,20201 1,0100502 1,0100502
2 0,2 0,202010033 0,3060452 0,3076057 0,416324296 1,0408108 1,0408108
3 0,3 0,416324308 0,5308135 0,5336757 0,656507005 1,0941743 1,0941743
4 0,4 0,656504559 0,7888996 0,7935335 0,93882209 1,1735108 1,1735109
5 0,5 0,938808651 1,0984061 1,105588 1,284069614 1,2840253 1,2840254
6 0,6 1,284025256 1,4830492 1,4939955 1,720109765 1,433329 1,4333294
7 0,7 1,719994793 1,9751274 1,991711 2,285500128 1,6323152 1,6323162
8 0,8 2,285241262 2,6198659 2,6449627 3,034898335 1,8964785 1,8964809
9 0,9 3,034365548 3,4819345 3,5199778 4,047257249 2,2479026 2,247908
10 1 4,046224662 4,6554063 4,7132785 5,438460884 2,7182702 2,7182818
(c) Aproxime )
5
.
0
(
y
.
1
)
5
.
0
(
2
)
5
.
0
(

 e
y
.
1
)
5
.
0
( 
y
El error relativo porcentual que se cometió al aplicar la formula de Euler esta dado
por:
Er = %
000779
.
0
100
28403
.
1
28402
.
1
28403
.
1
100
*






p
p
p

55
0
0,5
1
1,5
2
2,5
3
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 xi
y
Solución numérica
Vemos que se ha obtenido una aproximación casi perfecta con este método,
reduciendo el error relativo verdadero de un 0.044% hasta un 0.000779%.
5.4. SISTEMAS DE ECUACIONES DIFERENCIALES ORDINARIAS.
Este tema está dedicado a la discusión de sistemas de ecuaciones diferenciales
ordinarias simultáneas. Dichos sistemas aparecen en problemas que tienen
relación con varias variables dependientes que son función de la misma variable
independiente.
)
,
,
,
,
( 2
1
1
1
n
x
x
x
t
f
dt
dx


)
,
,
,
,
(
)
,
,
,
,
(
2
1
2
1
2
2
n
n
n
n
x
x
x
t
f
dt
dx
x
x
x
t
f
dt
dx





Donde el problema consiste en averiguar quienes son )
(
,
,
)
(
),
( 2
1 t
x
t
x
t
x n
 que
satisfacen las ecuaciones diferenciales dadas. La solución de este sistema
requiere que se conozcan n condiciones iniciales en el valor de t.

56
Método de Runge – Kutta para sistemas de ecuaciones diferenciales
ordinarias:
Las ecuaciones obtenidas para el método Runge-Kutta de cuarto orden aplicado a
la solución de una ecuación diferenciales se pueden ampliar y utilizar para
solucionar sistemas de ecuaciones diferenciales de primer orden. Por ejemplo:
)
,
,
(
1 y
x
t
f
dt
dx
 0
0 )
( x
t
x 
)
,
,
(
1 y
x
t
f
dt
dy
 0
0 )
( y
t
y 
Entonces el método RK4 para este problema esta dado por la siguiente ecuación:
)
2
2
(
6
4
3
2
1
1 m
m
m
m
h
x
x n
n 





)
2
2
(
6
4
3
2
1
1 k
k
k
k
h
y
y n
n 





donde:
)
,
,
(
1
1 n
n
n y
x
t
f
m  )
,
,
(
2
1 n
n
n y
x
t
f
k 









 1
1
1
2
2
,
2
,
2
k
h
y
m
h
x
h
t
f
m n
n
n 








 1
1
2
2
2
,
2
,
2
k
h
y
m
h
x
h
t
f
k n
n
n









 2
2
1
3
2
,
2
,
2
k
h
y
m
h
x
h
t
f
m n
n
n 








 2
2
2
3
2
,
2
,
2
k
h
y
m
h
x
h
t
f
k n
n
n
)
,
,
( 3
3
1
4 hk
y
hm
x
h
t
f
m n
n
n 


 )
,
,
( 3
3
2
4 hk
y
hm
x
h
t
f
k n
n
n 



Ejemplo:
Dado el siguiente sistema de ecuaciones diferenciales con las condiciones
iniciales dadas:
x
dt
dx
5
.
0

 , 4
)
0
( 
x
y
x
dt
dy
3
.
0
1
.
0
4 

 , 6
)
0
( 
y
(a) Si analíticamente se encontró que t
e
C
t
x 5
.
0
1
2
)
( 
 y
3
40
)
( 3
.
0
2
5
.
0
1 

 
 t
t
e
C
e
C
t
y es la solución general del sistema, encuentre una
solución particular con las condiciones iniciales dadas.

57
(b) Resuelva numéricamente utilizando el método de Runge-Kutta de cuarto orden
en el intervalo de x = 0 a 5 y tamaño de paso 0.5
(c) Grafique y compare los resultados numéricos con los analíticos.
(a) Solución particular:
t
e
C
t
x 5
.
0
1
2
)
( 
 2
4
2 1
0
1 


 C
e
C
3
40
)
( 3
.
0
2
5
.
0
1 

 
 t
t
e
C
e
C
t
y
3
28
3
40
2
6
6
3
40
2
)
( 2
0
2
0










 C
e
C
e
t
y
t
e
t
x 5
.
0
4
)
( 
 ;
3
40
3
28
2
)
( 3
.
0
5
.
0


 
 t
t
e
e
t
y
Aplicamos el método de Runge-Kutta de cuarto orden, de 0 a 5 con tamaño de
paso 0.5
Condiciones iniciales:
4
0 

 x
t , 6
0 

 y
t , )
6
,
4
,
0
(
Aplicamos las ecuaciones del método:
2
)
4
(
5
.
0
)
4
(
)
( 1
0
1
1 




 f
x
f
m
8
.
1
)
6
(
3
.
0
)
4
(
1
.
0
4
)
6
,
4
(
)
,
( 2
0
0
2
1 




 f
y
x
f
k
75
.
1
)
5
.
3
(
5
.
0
)
5
.
3
(
)
2
(
2
5
.
0
4
2
1
1
1
0
1
2 




















 f
f
m
h
x
f
m
)
45
.
6
,
5
.
3
(
8
.
1
2
5
.
0
6
),
2
(
2
5
.
0
0
2
,
2
2
2
1
0
1
0
2
2 f
f
k
h
y
m
h
x
f
k 



















715
.
1
)
45
.
6
(
3
.
0
)
5
.
3
(
1
.
0
4 



78125
.
1
)
5625
.
3
(
5
.
0
)
5625
.
3
(
)
75
.
1
(
2
5
.
0
4
2
1
1
2
0
1
3 




















 f
f
m
h
x
f
m


















 715
.
1
2
5
.
0
6
),
75
.
1
(
2
5
.
0
0
2
,
2
2
2
0
2
0
2
3 f
k
h
y
m
h
x
f
k
715125
.
1
)
42875
.
6
(
3
.
0
)
5625
.
3
(
1
.
0
4
)
42875
.
6
,
5625
.
3
(
2 




 f
554688
.
1
)
109375
.
3
(
5
.
0
))
78125
.
1
(
5
.
0
4
(
)
( 1
3
0
1
4 








 f
m
h
x
f
m
)
715125
.
1
5
.
0
6
),
78125
.
1
(
5
.
0
4
(
)
,
( 2
3
0
3
0
2
4 








 f
k
h
y
m
h
x
f
k

58
631794
.
1
)
857563
.
6
(
3
.
0
)
109375
.
3
(
1
.
0
4
)
857563
.
6
,
109375
.
3
(
2
4 



 f
k
)
554688
.
1
)
78125
.
1
(
2
)
75
.
1
(
2
2
(
6
5
.
0
4
)
2
2
(
6
4
3
2
1
0
1 











 m
m
m
m
h
x
x
115234
.
3
1 
x
)
631794
.
1
)
71525
.
1
(
2
)
715
.
1
(
2
8
.
1
(
6
5
.
0
6
)
2
2
(
6
4
3
2
1
0
1 








 k
k
k
k
h
y
y
857670
.
6
1 
y
Resumimos todos los resultados en las siguientes tablas:
Tabla: Valores de las pendientes:
t m1 k1 m2 k2 m3 k3 m4 k4
0
0,5 -2 1,8 -1,75 1,715 -1,78125 1,715125 -1,5546875 1,6317938
1 -1,55761719 1,631175469 -1,36291504 1,547777738 -1,38725281 1,549165 -1,210804 1,4681634
1,5 -1,21308565 1,467751168 -1,06144994 1,387996971 -1,08040441 1,3901876 -0,9429845 1,3132432
2 -0,94476153 1,312981901 -0,82666634 1,238127297 -0,84142824 1,240789 -0,7344045 1,168935
2,5 -0,7357884 1,16878279 -0,64381485 1,099518791 -0,65531154 1,1024143 -0,5719605 1,0361862
3 -0,57303833 1,036111927 -0,50140854 0,97272949 -0,51036226 0,9756924 -0,4454478 0,9152762
3,5 -0,44628717 0,915256359 -0,39050128 0,857769311 -0,39747451 0,8606862 -0,3469185 0,8060272
4 -0,34757229 0,806044473 -0,30412575 0,754280445 -0,30955657 0,7570766 -0,2701831 0,7079608
4,5 -0,27069228 0,70800249 -0,23685575 0,661669611 -0,24108532 0,6642987 -0,210421 0,620412
5 -0,21081748 0,620468677 -0,18446529 0,579203963 -0,18775932 0,58164 -0,1638776 0,5426106
Tabla: Soluciones numérica y analítica:
t xi yi xanalitica (*) yanalitica (**)
0 4 6 4 6
0,5 3,1152344 6,8576703 3,1152031 6,8576605
1 2,4261713 7,6321057 2,4261226 7,6320913
1,5 1,8895231 8,326886 1,8894662 8,3268704
2 1,4715768 8,9468651 1,4715178 8,9468503
2,5 1,1460767 9,4976014 1,1460192 9,4975884
3 0,8925743 9,984954 0,8925206 9,9849435
3,5 0,6951446 10,414804 0,6950958 10,414796
4 0,5413846 10,792864 0,5413411 10,792858
4,5 0,421635 11,124559 0,4215969 11,124556
5 0,3283729 11,414957 0,32834 11,414955
(*) t
e
t
x 5
.
0
4
)
( 
 ; (**)
3
40
3
28
2
)
( 3
.
0
5
.
0


 
 t
t
e
e
t
y
(c) Grafique y compare los resultados

59
0
2
4
6
8
10
12
0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5
t
x,y
X numérica X analítica
Y numérica Y analitica
Vemos que la solución numérica del método de Runge-Kutta de cuarto orden es
muy buena.
ACTIVIDAD No. 13
1. Dada la siguiente ecuación diferencial y
yx
dx
dy
1
.
1
2

 con la condición inicial:
1
)
0
( 
y ,
(b) Resuelva numéricamente aplicando los tres métodos estudiados en el
intervalo de x = 0 a 2 con tamaño de paso 0.1
(c) Aproxime )
5
.
1
(
y
2. Dada la siguiente ecuación diferencial y
e
dx
dy x
5
.
0
4 8
.
0

 con la condición
inicial: 2
)
0
( 
y ,

60
(a) Si analíticamente se encontró que x
x
Ce
e
x
y 5
.
0
8
.
0
13
40
)
( 

 es la solución
general del sistema, encuentre una solución particular con las condiciones
iniciales dadas.
intervalo de x = 0 a 4 con tamaño de paso 0.5
(c) Aproxime )
5
.
2
(
y
(d) Grafique y compare los resultados numéricos con los analíticos.
3. Dada la siguiente ecuación diferencial t
sen
y
dt
dy 3
 con la condición inicial:
1
)
0
( 
y ,
intervalo de t = 0 a 1 con tamaño de paso 0.1
(c) Aproxime )
5
.
1
(
y
4. Un modelo lineal para un péndulo oscilante esta dado el siguiente sistema de
ecuaciones diferenciales con las condiciones iniciales dadas:
y
dt
dx
 , 0
)
0
( 
x
x
dt
dy
16

 , 0
)
0
( 
y
(a) Si analíticamente se encontró que )
4
(
4
1
)
4
cos(
4
1
)
( 2
1 t
sen
C
t
C
t
x 

 y
)
4
cos(
)
4
(
)
( 2
1 t
C
t
sen
C
t
y 
 es la solución general del sistema, encuentre una
solución particular con las condiciones iniciales dadas.
(b) Resuelva numéricamente utilizando el método de Runge-Kutta de cuarto orden
en el intervalo de x = 0 a 4 y tamaño de paso 0.5
(c) Grafique y compare los resultados numéricos con los analíticos.
5. Diseñe hojas de cálculo para aplicar los tres métodos estudiados. Elabore un
diagrama de flujo y escriba programas que apliquen los tres métodos
estudiados.

Guia de estudio 5 (tema 5 ecuaciones diferenciales ordinarias)

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Similar a Guia de estudio 5 (tema 5 ecuaciones diferenciales ordinarias)

Similar a Guia de estudio 5 (tema 5 ecuaciones diferenciales ordinarias) (20)

Último

Último (20)

Guia de estudio 5 (tema 5 ecuaciones diferenciales ordinarias)