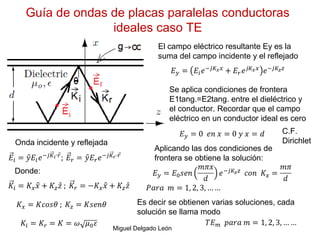
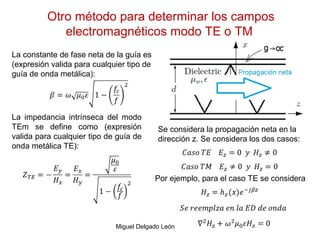
Este documento describe las ondas guiadas en placas paralelas conductoras ideales para el caso TE. Explica que el campo eléctrico resultante es la suma del campo incidente y reflejado, y que al aplicar las condiciones de frontera entre el dieléctrico y el conductor se obtienen varias soluciones llamadas modos. También describe cómo calcular la frecuencia de corte, la impedancia intrínseca y la atenuación para cada modo TE.