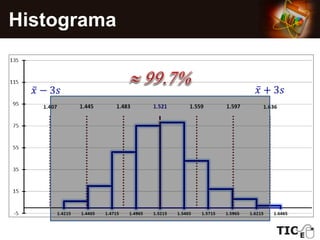
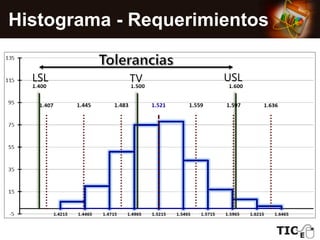
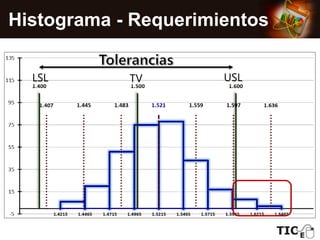
El documento describe cómo construir e interpretar un histograma para analizar los datos de diámetros de esferas metálicas. Se muestran los pasos para crear el histograma de una muestra de 300 piezas, calcular su media y desviación estándar, y comparar los resultados con las especificaciones del cliente. El análisis revela que la media de la muestra es ligeramente mayor que el valor deseado, aunque la diferencia está dentro de la tolerancia, pero el 4% de la muestra se encuentra fuera del límite superior permitido.

1. Histograms and
Variability
G. Edgar Mata Ortiz

2. Histograma
• El histograma es una herramienta gráfica
para la organización y presentación de
datos.
• Está formado por barras cuya altura
representa la frecuencia absoluta de cada
categoría.
• Es necesario que en el eje equis se
representen los límites entre categorías.
• Las barras no presentan ninguna
separación entre ellas.

3. Histograma
• Para facilitar el análisis de la información se
recomienda que el histograma, además de las
barras, contenga:
1. Una línea en la posición de la media aritmética: 𝒙
2. Tres líneas en las posiciones de la media
aritmética más una, dos y tres desviaciones
estándar: 𝒙 + 𝟏𝒔, 𝒙 + 𝟐𝒔 y 𝒙 + 𝟑𝒔
3. Tres líneas en las posiciones de la media
aritmética menos una, dos y tres desviaciones
estándar: 𝒙 − 𝟏𝒔, 𝒙 − 𝟐𝒔 y 𝒙 − 𝟑𝒔

4. Histograma
• En las siguientes diapositivas se plantea un
problema y se resuelve, paso a paso,
mediante un histograma y su análisis.
• Es conveniente ir resolviendo el mismo
ejemplo utilizando sólo una calculadora
para una mejor comprensión del
procedimiento.
• La fase de análisis es la más importante, ya
que la construcción del histograma puede,
posteriormente, realizarse mediante algún
software estadístico.

5. Problema
• Una característica
importante en la
fabricación de ciertos
opresores es el diámetro
de la esfera metálica que
actúa como seguro.
• El cliente está solicitando
que las esferas tengan un
diámetro de 1.5 mm con
una tolerancia de 0.1 mm.
TV = 1.5 ± 0.1 mm.

6. Problema
• Se te indica que realices un análisis
estadístico para determinar si se están
cumpliendo las especificaciones del
cliente.

7. Problema
• De un lote grande se toma una muestra
de 300 piezas para verificar que cumplan
con las especificaciones del cliente.
• Determina si la muestra cumple con las
especificaciones del cliente y calcula la
tasa de defectos en la muestra.
• Estima la tasa de defectos en el lote
completo.

8. Problema
• En la siguiente tabla se encuentran los
diámetros de las 300 piezas de la
muestra.

9. Datos
1.507 1.470 1.524 1.502 1.502 1.514 1.490 1.501 1.489 1.590 1.470 1
1.579 1.533 1.551 1.501 1.514 1.500 1.527 1.505 1.496 1.526 1.548 1
1.530 1.498 1.468 1.519 1.460 1.534 1.572 1.486 1.533 1.579 1.472 1
1.441 1.462 1.481 1.567 1.544 1.508 1.503 1.581 1.514 1.502 1.518 1
1.537 1.515 1.482 1.519 1.494 1.485 1.473 1.604 1.565 1.476 1.479 1
1.587 1.529 1.491 1.542 1.549 1.535 1.529 1.424 1.610 1.507 1.466 1
1.506 1.504 1.503 1.579 1.562 1.525 1.487 1.540 1.569 1.521 1.490 1
1.520 1.508 1.537 1.529 1.503 1.555 1.494 1.484 1.527 1.509 1.567 1
1.487 1.469 1.608 1.507 1.486 1.502 1.534 1.544 1.524 1.503 1.501 1
1.481 1.470 1.494 1.483 1.519 1.511 1.566 1.547 1.518 1.470 1.495 1
1.538 1.545 1.512 1.516 1.559 1.553 1.534 1.464 1.608 1.547 1.539 1
1.485 1.566 1.538 1.525 1.543 1.545 1.523 1.535 1.486 1.517 1.489 1
1.522 1.528 1.527 1.587 1.487 1.462 1.512 1.470 1.553 1.484 1.464 1
1.537 1.477 1.528 1.515 1.518 1.505 1.566 1.478 1.490 1.570 1.500 1
1.495 1.582 1.550 1.472 1.507 1.500 1.472 1.513 1.530 1.473 1.526 1

10. Datos
70 1.514 1.536 1.539 1.541 1.518 1.527 1.522 1.524 1.562
48 1.490 1.514 1.512 1.544 1.482 1.511 1.534 1.534 1.549
72 1.566 1.515 1.561 1.537 1.541 1.566 1.492 1.577 1.482
18 1.549 1.473 1.457 1.538 1.599 1.460 1.439 1.523 1.529
79 1.500 1.486 1.539 1.592 1.547 1.522 1.519 1.470 1.466
66 1.524 1.552 1.500 1.525 1.527 1.502 1.543 1.559 1.485
90 1.511 1.482 1.533 1.520 1.549 1.529 1.556 1.535 1.597
67 1.601 1.521 1.605 1.541 1.463 1.503 1.509 1.479 1.520
01 1.549 1.556 1.536 1.510 1.508 1.530 1.540 1.622 1.504
95 1.536 1.594 1.542 1.530 1.526 1.520 1.581 1.578 1.467
39 1.524 1.510 1.538 1.562 1.553 1.558 1.550 1.480 1.556
89 1.498 1.480 1.572 1.494 1.509 1.520 1.513 1.498 1.526
64 1.489 1.534 1.519 1.441 1.562 1.425 1.528 1.535 1.503
00 1.494 1.511 1.551 1.556 1.586 1.468 1.552 1.579 1.493
26 1.446 1.535 1.532 1.638 1.522 1.558 1.508 1.486 1.558

11. Histograma
• Se agrupan los datos en 9 intervalos.
• El valor máximo es: 1.638 mm
• El valor mínimo: 1.424 mm
• El rango es: 0.214
• El tamaño del intervalo aparente es de:
0.024 mm
• El tamaño del intervalo real es: 0.025 mm
• La tabla de análisis estadístico se
encuentra en la siguiente diapositiva.

12. Tabla de análisis estadístico
Lím. Inferior Lím. Superior xi fi fai fri frai fi por xi
1.4170 1.4420 1.4295 5 5 0.0167 0.0167 7.14750 0.45875 0.04209
1.4420 1.4670 1.4545 11 16 0.0367 0.0533 15.99950 0.73425 0.04901
1.4670 1.4920 1.4795 51 67 0.1700 0.2233 75.45450 2.12925 0.08890
1.4920 1.5170 1.5045 68 135 0.2267 0.4500 102.30600 1.13900 0.01908
1.5170 1.5420 1.5295 86 221 0.2867 0.7367 131.53700 0.70950 0.00585
1.5420 1.5670 1.5545 48 269 0.1600 0.8967 74.61600 1.59600 0.05307
1.5670 1.5920 1.5795 19 288 0.0633 0.9600 30.01050 1.10675 0.06447
1.5920 1.6170 1.6045 10 298 0.0333 0.9933 16.04500 0.83250 0.06931
1.6170 1.6420 1.6295 2 300 0.0067 1.0000 3.25900 0.21650 0.02344
0
#N/A #N/A #N/A #N/A
#N/A #N/A
#N/A #N/A #N/A #N/A
#N/A #N/A #N/A #N/A
#N/A #N/A #N/A #N/A
#N/A #N/A #N/A #N/A
Totales 456.375 8.92 0.42
1.5213
0.02974
0.00139
0.037265
Clases o categorías Marcas
de clase
Frecuencias
Medidas de tendencia central y
dispersiónIntervalos
s2
=
s =
− −

13. Histograma
Por el aspecto visual del
histograma podemos afirmar que
la muestra está distribuida en
forma aproximadamente normal.

14. Histograma
Por el aspecto visual del
histograma podemos afirmar que
la muestra está distribuida en
forma aproximadamente normal.

15. Histograma
Eje y: Frecuencia absoluta
Eje x: Límites entre clases o categorías
Por el aspecto visual del
histograma podemos afirmar que
la muestra está distribuida en
forma aproximadamente normal.

16. Histograma
Eje x: Límites entre clases o categorías
Se amplía para observar
cómo se traza la escala en
el eje x (horizontal).

17. Histograma
• Para analizar el comportamiento de la
muestra, es necesario representar con
líneas verticales, los siguientes valores:
+ 1𝑠 1.559
+ 2𝑠 1.597
+ 3𝑠 1.636
1.521
− 1𝑠 1.483
− 2𝑠 1.445
− 3𝑠 1.407

18. Histograma
Media y desviación estándar

19. Histograma
Media y desviación estándar
+ 1𝑠 + 2𝑠 + 3𝑠− 3𝑠 − 2𝑠 − 1𝑠

20. Regla empírica
• Los valores de la media y desviación
estándar son importantes para la aplicación
de la regla empírica o cualquier método de
estadística inferencial.

21. Histograma
• Aproximadamente el 68% de los datos se
encuentran entre la media menos una
desviación estándar y la media más una
desviación estándar.

22. Histograma
+ 1𝑠− 1𝑠

23. Histograma
• Aproximadamente el 95% de los datos se
encuentran entre la media menos dos
desviaciones estándar y la media más dos
desviaciones estándar.

24. Histograma
+ 2𝑠− 2𝑠

25. Histograma
• Aproximadamente el 99.7% de los datos se
encuentran entre la media menos tres
desviaciones estándar y la media más tres
desviaciones estándar.

26. Histograma
+ 3𝑠− 3𝑠

27. Histograma
• Por lo tanto, aproximadamente el 0.3% de
los datos se encuentra fuera del intervalo:
− 3𝑠, + 3𝑠

28. Histograma
• En las diapositivas anteriores se analizó la
variabilidad de los datos sin compararlos
con nada, solamente su variabilidad
interna.
• Sin embargo, un aspecto fundamental es
la comparación de la muestra contra el
valor deseado, es decir, contra las
especificaciones del cliente.
• En este caso el valor deseado es: 1.5 𝑚𝑚

29. Histograma
• Comparamos la media contra el valor
deseado:
• La media: 1.521 es ligeramente mayor
(0.021 mm) que el valor deseado: 1.5 𝑚𝑚

30. Histograma: Requerimientos
TV: Target Value (Valor deseado)
Una diferencia de 0.021 mm

31. Histograma
• Comparamos la media contra el valor
deseado:
• La media: 1.521 es ligeramente mayor
(0.021 mm) que el valor deseado: 1.5 𝑚𝑚
¿Esta diferencia es
grande o pequeña?
¿El producto
cumple con las
especificaciones del
cliente?

32. Histograma
• Para responder a esta pregunta
necesitamos revisar otro dato:
• La tolerancia. Recordemos que el valor
deseado es: TV 1.5 𝑚𝑚 ± 0.1 𝑚𝑚
¿Esta diferencia es
grande o pequeña?
¿El producto
cumple con las
especificaciones del
cliente?

33. Histograma - Requerimientos
TV

34. Histograma - Requerimientos
TV USLLSL

35. Histograma - Requerimientos
• Podemos observar que algunas de las
barras del histograma quedan fuera del USL
(Upper Specification Limit = Límite Superior
de Especificación)

36. Histograma - Requerimientos
• Podemos observar que algunas de las
barras del histograma quedan fuera del USL
(Upper Specification Limit = Límite Superior
de Especificación)
Esto significa que algunas
piezas no cumplen con
las especificaciones del
cliente, son más grandes
que el valor máximo
considerado aceptable.

37. Histograma - Requerimientos
TV USLLSL

38. Histograma - Requerimientos
• Observando cuidadosamente la gráfica se aprecia que +
2𝑠 queda justo dentro de la tolerancia, y las restantes dos
barras del histograma se salen del USL.
• Estas dos barras representan el 3.33+0.67 = 4%.
Según la regla empírica,
aproximadamente el 95% de los
datos están dentro de ± dos
desviaciones estándar, entonces el
5% queda fuera de este intervalo,
pero como sólo se trata de un lado
del histograma, el 2.5% de los datos
estarán fuera del USL.

39. Histograma - Requerimientos
• Como te habrás dado cuenta, lo que indica la regla
empírica:
• El 2.5% de los datos estarán fuera de especificación
• No coincide con los cálculos de la tabla de análisis
estadístico:
• Estas dos barras representan el: 3.33+0.67 = 4%.
No coinciden porque la regla empírica
indica probabilidades (2.5%), mientras
que la tabla de análisis estadístico son
valores reales de una muestra
específica (4%).

40. Histograma - Requerimientos
• Para este cliente el TV 1.5 𝑚𝑚 ± 0.1 𝑚𝑚
• De acuerdo con la muestra tendremos una tasa de
defectos entre el 2.5% y el 4%
• Este porcentaje de defectos es demasiado alto, será
necesario revisar el proceso y tomar acciones para reducir
la variabilidad del proceso.
La variabilidad es inevitable,
siempre se presenta, el objetivo
es mantenerla bajo control,
reducirla hasta límites que
mantengan el producto dentro de
las especificaciones del cliente.

41. Cliente número 2.
La empresa tiene otro cliente cuyos
requerimientos son de una mayor
tolerancia:
TV 1.5 𝑚𝑚 ± 0.15 𝑚𝑚

42. Histograma
• Este segundo cliente, al permitir que los
productos tengan mayor tolerancia, es más
probable cumplir con sus requerimientos.
• Si empleamos la misma muestra el histograma
queda igual, solamente se modifican los límites
de especificación.
TV 1.5 𝑚𝑚 ± 0.15 𝑚𝑚
𝑈𝑆𝐿 1.65 𝑚𝑚
𝐿𝑆𝐿 1.35 𝑚𝑚

43. Histograma - Requerimientos
TV USLLSL

44. Histograma - Requerimientos
• En este caso, todas las piezas de la muestra
están dentro de las especificaciones.

45. Histograma - Requerimientos
• En este caso, todas las piezas de la muestra
están dentro de las especificaciones.
A pesar de que todas las
piezas de la muestra
cumplen con las
especificaciones, no
debemos olvidar la regla
empírica.
La recta + 3𝑠 está
demasiado cerca del USL.

46. Histograma - Requerimientos
TV USLLSL

47. Histograma - Requerimientos
• Al estar la recta + 3𝑠 tan cerca del USL,
existe una probabilidad del 0.15% de que
se presenten piezas defectuosas.
El proceso debe ser
supervisado cuidadosa y
atentamente para evitar
que haya piezas
defectuosas.

48. La variabilidad es un concepto muy
importante en el control estadístico
del proceso.
En las siguientes diapositivas se
abordará el tema de la variabilidad,
sus causas y su manejo.
Variabilidad del proceso

49. Histograma

50. Variabilidad del proceso
Small changes
Product
Quality

51. Variabilidad del proceso
La variabilidad es la consecuencia de pequeños
e inevitables cambios en el proceso, que
afectan a la calidad del producto

52. Variabilidad del proceso

53. Causas de la variabilidad
• Causas comunes
• Son inherentes al proceso
• Son inevitables
• Se distribuyen en forma normal
• También se llaman causas aleatorias

54. • Causas especiales
• También se llaman causas asignables
• No son parte normal del proceso
• Pueden ser identificadas, seguidas y eliminadas
• No son aleatorias
• La identificación y seguimiento se lleva a cabo mediante
herramientas estadísticas
Causas de la variabilidad

55. • Referencias:
licmata@hotmail.com
https://sites.google.com/site/mataspc/home
http://licmata-math.blogspot.com/
http://www.scoop.it/t/mathematics-learning
http://www.slideshare.net/licmata/
http://www.facebook.com/licemata
Twitter: @licemata
Gracias por su atención