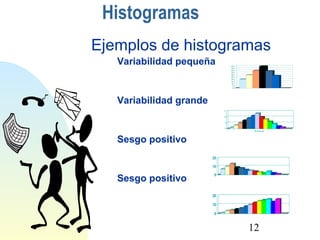
Este documento explica qué son los histogramas y cómo se usan. Los histogramas son gráficos que resumen conjuntos de datos agrupándolos en intervalos para mostrar la distribución de valores. Muestran patrones y comportamientos que son difíciles de ver en tablas numéricas. Se usan para analizar grandes cantidades de datos y revelar la variabilidad de procesos.

1. 1
Solución de problema
Herramientas aplicables
90
80
70
60
50
40
30
Histogramas 0
20
10
1er trim. 2do trim. 3er trim. 4to trim.
Este
Oeste
Norte

2. Que al finalizar la sesión,
los asistentes sean
capaces de comprender
la herramienta:
Histogramas
2
OBJETIVO

3. 3
Histogramas
Un histograma es un resumen
gráfico de un conjunto de datos.
Su éxito radica en que conjuga dos
tipos de técnicas:
la estadística
permite sacar conclusiones del conjunto
de los datos.
y los gráficos
(permite representar los datos y hace
sencilla su interpretación.

4. 4
Histogramas
El objetivo de los histogramas
es estudiar la capacidad de
los procesos y mantenerlos
bajo control.
Nos permite ver esquemas y
comportamientos que son
difíciles de captar en una
tabla numérica.

5. 5
Histogramas
Los histogramas, o histogramas de
frecuencia son una herramienta útil cuando
hay que analizar una gran cantidad de
datos.
Para mostrar en forma de gráficos de barras las
características de un producto o servicio
• tipos de defectos, problemas, riesgos de
seguridad, etc.
Un histograma toma datos de mediciones
• temperatura, presiones, alturas, pesos, etc.
• muestra su distribución.
Un histograma revela la cantidad de variación
propia de un proceso.
50
45
40
35
30
25
20
15
10
0 5
1er trim.
A
B
C
E
F
G
H
c

6. 6
Histogramas
Se recogen los datos que se
necesitan por el método más
adecuado.
Los datos son fundamentales
para toda acción de mejora.
Tener en cuenta que datos no
es igual que información.

7. 7
Histogramas
Se clasifican los datos en una
serie de grupos representativos.
Una misma característica
(ejemplo: altura)
agrupada por intervalos (ejemplo:
entre 5 y 10 cm.)

8. Se construye el histograma.
8
Histogramas
50
45
40
35
30
25
20
15
10
0 5
Alturas de cajas
A
B
C
E
F
G
H
c

9. Se interpreta el histograma
para extraer toda la
información que se necesite.
Clasificación de cajas de embalaje según
9
Histogramas
50
40
30
20
10
0
Cantidad de cajas
su altura
cm
Altura de cajas
A= 15
B= 16
C= 17
E= 18
F= 19
G= 20
H= 21
c

10. En el histograma del ejemplo
anterior la mayor cantidad de
unidades se encuentran en el
centro, y aproximadamente
una cantidad igual de
unidades se distribuye a
ambos lados.
Es una distribución tipo:
NORMAL o GAUSIANA (forma
de campana)
10
Histogramas

11. Es importante saber lo siguiente:
Si la dispersión de la distribución cae
dentro de las especificaciones. Si no
es así, qué cantidad cae fuera de las
mismas (VARIABILIDAD)
Si la distribución está centrada en el
lugar debido. Podemos saber si la
mayoría de los datos caen en el lado
alto o en el lado bajo (SESGO)
11
Histogramas

12. Ejemplos de histogramas
Variabilidad pequeña
50
45
40
35
30
25
20
15
10
5
Variabilidad grande
15
10
5
Sesgo positivo
20
10
Sesgo positivo
12
Histogramas
0
0
Alturas de cajas
0
20
10
0

13. Problemas de interpretación de los histogramas
Errores a evitar
Contentarse con pocos datos.
Considerarlo sólo como instrumento
de representación y no de análisis.
Confundirlo con el diagrama de
Pareto.
13