1. La función se evalúa para determinar si cuatro funciones son pares o impares. La respuesta correcta es que f(x) y h(x) son pares, g(x) es impar y k(x) es par. 2. Se evalúa si una función es creciente o decreciente en diferentes intervalos. La respuesta correcta es que f(x) es decreciente si x pertenece a ]-∞,2]. 3. Otra función se evalúa para determinar si es creciente o decreciente. La respuesta correcta es que f(x

1. ESCUELAPOLITÉCNICANACIONAL
DEPARTAMENTO DE FORMACIÓN BÁSICA
FUNDAMENTOS DE MATEMÁTICA
CORECCIÓN DE LAPRUEBAN°2
2016 A GR11 2016-07-14
1. Sean las funciones 𝑓( 𝑥) = 𝑥2
− 5, 𝑔( 𝑥) = −𝑥, ℎ( 𝑥) = | 𝑥|, 𝑘( 𝑥) = √
| 𝑥2 −1|
𝑥2 +1
Entonces:
a) 𝑓( 𝑥) 𝑝𝑎𝑟, 𝑔( 𝑥) 𝑝𝑎𝑟,ℎ( 𝑥) 𝑝𝑎𝑟, 𝑘( 𝑥) 𝑝𝑎𝑟
b) 𝑓( 𝑥) 𝑝𝑎𝑟, 𝑔( 𝑥) 𝑖𝑚𝑝𝑎𝑟,ℎ( 𝑥)𝑖𝑚𝑝𝑎𝑟, 𝑘( 𝑥) 𝑝𝑎𝑟
c) 𝑓( 𝑥) 𝑝𝑎𝑟, 𝑔( 𝑥) 𝑖𝑚𝑝𝑎𝑟,ℎ( 𝑥) 𝑝𝑎𝑟, 𝑘( 𝑥) 𝑝𝑎𝑟
d) 𝑓( 𝑥) 𝑝𝑎𝑟, 𝑔( 𝑥) 𝑝𝑎𝑟,ℎ( 𝑥) 𝑝𝑎𝑟, 𝑘( 𝑥) 𝑖𝑚𝑝𝑎𝑟
Justificación:
𝑓( 𝑥) = 𝑥2
− 5
𝑓(−𝑥) = (− 𝑥)2 − 5
𝑓(−𝑥) = 𝑥2
− 5
𝑓(−𝑥) = 𝑓( 𝑥)
∴ 𝑓( 𝑥) 𝑒𝑠 𝑝𝑎𝑟
𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑐) 𝑓( 𝑥) 𝑝𝑎𝑟, 𝑔( 𝑥) 𝑖𝑚𝑝𝑎𝑟,ℎ( 𝑥) 𝑝𝑎𝑟, 𝑘( 𝑥) 𝑝𝑎𝑟
ℎ( 𝑥) = | 𝑥|
ℎ( 𝑥) = |−𝑥|
ℎ( 𝑥) = |−1|| 𝑥|
ℎ( 𝑥) = | 𝑥|
ℎ(−𝑥) = ℎ(𝑥)
∴ ℎ( 𝑥) 𝑒𝑠 𝑝𝑎𝑟
𝑘( 𝑥) = √
| 𝑥2 − 1|
𝑥2 + 1
𝑘(−𝑥) = √
|(−𝑥)2 − 1|
(−𝑥)2 + 1
𝑘(−𝑥) = √
| 𝑥2 − 1|
𝑥2 + 1
𝑘(−𝑥) = 𝑘( 𝑥)
∴ 𝑘( 𝑥) 𝑒𝑠 𝑝𝑎𝑟
𝑔( 𝑥) = −𝑥
𝑔(−𝑥) = −(−𝑥)
𝑔(−𝑥) = 𝑥
𝑔(−𝑥) = −𝑔(𝑥)
∴ 𝑔( 𝑥) 𝑒𝑠 𝑖𝑚𝑝𝑎𝑟

2. 2. Sea la función 𝑓( 𝑥) = |6 − 3𝑥|
a) 𝑓( 𝑥) 𝑒𝑠 𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒, 𝑠𝑖 𝑥 ∈ ] − ∞,2]
b) 𝑓( 𝑥) 𝑒𝑠 𝑑𝑒𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒, 𝑠𝑖 𝑥 ∈ ] − ∞,2]
c) 𝑓( 𝑥) 𝑒𝑠 𝑑𝑒𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒, 𝑠𝑖 𝑥 ∈ [2,+∞[
d) 𝑓( 𝑥) 𝑒𝑠 𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒 𝑠𝑖 𝑥 ∈ [−2,+∞[
Justificación:
6 − 3𝑥 = 0
−3𝑥 = −6
𝑥 = 2
3. Sea 𝑓(𝑥) =
𝑥+2
𝑥−4
Se cumple que:
a) 𝑓( 𝑥) 𝑒𝑠 𝑑𝑒𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒, ∀ 𝑥 ∈ 𝑅 − {4}
b) 𝑓( 𝑥) 𝑒𝑠 𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒, 𝑠𝑖 𝑥 ∈ [−∞,4[
c) 𝑓( 𝑥) 𝑒𝑠 𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒, 𝑠𝑖 𝑥 ∈ ]4,+∞[
d) 𝑓( 𝑥) 𝑒𝑠 𝑑𝑒𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒, 𝑠𝑖 𝑥 ∈]4, +∞[
Justificación:
𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑑)𝑓( 𝑥) 𝑒𝑠 𝑑𝑒𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒 𝑠𝑖 𝑥 ∈]4,+∞[
2
4-2
𝐼2: ]4, +∞[
4 < 𝑥1 < 𝑥2
0 < 𝑥1 − 4 < 𝑥2 − 4
0 <
6
𝑥2 − 4
<
6
𝑥1 − 4
0 <
6
𝑥2 − 4
+ 1 <
6
𝑥1 − 4
+ 1
𝑓( 𝑥2) < 𝑓( 𝑥1)
𝑓( 𝑥) ↙ 𝑥 > 4
6 - 3x + -
I1: 𝑥 ∈ ] − ∞,2]
𝑓( 𝑥) = |6 − 3𝑥|
(+)
𝑓( 𝑥) = 6 − 3𝑥
𝑓( 𝑥) ↙ 𝑥 < 2
𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑏) 𝑓( 𝑥) 𝑒𝑠 𝑑𝑒𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒, 𝑠𝑖 𝑥 ∈ ] − ∞,2]
-∞ 2 ∞
𝑦 =
6
𝑥 − 4
+ 1

3. 4. Sean las funciones: 𝑓( 𝑥) = | 𝑥 − 3| 𝑠𝑖 𝑥 < 2, 𝑔( 𝑥) =
3𝑥−7
𝑥−1
𝑠𝑖 𝑥 > 1. 𝐸𝑙 𝑑𝑜𝑚𝑖𝑛𝑖𝑜 𝑑𝑒 𝑔𝑜𝑓 𝑒𝑠:
a) 𝑥 ∈ ]1,2[
b) 𝑥 ∈ ]−∞,2[
c) 𝑥 ∈ ]4, +∞[
d) 𝑥 ∈ ]−∞,4[
Justificación:
𝑔𝑜𝑓( 𝑥) = 𝑔[ 𝑓( 𝑥)]
𝑔𝑜𝑓( 𝑥) =
3| 𝑥 − 3| − 7
| 𝑥 − 3| − 1
| 𝑥 − 3| > 1 ∧ 𝑥 < 2
(𝑥 − 3 > 1 ∨ 𝑥 − 3 < −1) ∧ 𝑥 < 2
(𝑥 > 4 ∨ 𝑥 < 2 ) ∧ 𝑥 < 2
- ∞ ∞
𝑥 ∈] − ∞,2[
𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑏)𝑥 ∈ ]−∞,2[
5. Sea 𝑓: ]−∞,3] → 𝐵
𝑥 → 𝑓( 𝑥) = 𝑥2 − 6𝑥 − 7
𝐼𝑛𝑦𝑒𝑐𝑡𝑖𝑣𝑎. 𝐿𝑎 𝑓𝑢𝑛𝑐𝑖ó𝑛 𝑓−1 𝑦 𝑠𝑢 𝑑𝑜𝑚𝑖𝑛𝑖𝑜 𝑒𝑠:
a) 𝑓−1( 𝑥) = 3 − √ 𝑥 + 16 𝑠𝑖 𝑥 ≥ −16
b) 𝑓−1( 𝑥) = 3 + √ 𝑥 + 16 𝑠𝑖 𝑥 ≥ −16
c) 𝑓−1( 𝑥) = −3 − √ 𝑥 + 16 𝑠𝑖 𝑥 ≥ −16
d) 𝑓−1( 𝑥) = 3 − √ 𝑥 + 16 𝑠𝑖 𝑥 ≤ −16
Justificación:
𝑦 = 𝑥2 − 6𝑥 − 7
𝑦 = ( 𝑥 − 3)2 − 16
𝑥 ≤ 3
( 𝑥 − 3) ≤ 0
( 𝑥 − 3)2 ≥ 0
( 𝑥 − 3)2 − 16 ≥ −16
𝑅𝑓: 𝑦 ≥ −16
𝐵 = 𝑅𝑓
2 4
𝑓: ] − ∞,3] → [−16,+∞[
𝑥 → 𝑓( 𝑥) = 𝑥2 − 6𝑥 − 7
∴ 𝑓 𝑒𝑠 𝑖𝑛𝑦𝑒𝑐𝑡𝑖𝑣𝑎
∴ 𝑓 𝑒𝑠 𝑠𝑜𝑏𝑟𝑒𝑦𝑒𝑐𝑡𝑖𝑣𝑎
∴ 𝑓 𝑒𝑠 𝑏𝑖𝑦𝑒𝑐𝑡𝑖𝑣𝑎
∴ ∃ 𝑓−1

4. 𝑦 = ( 𝑥 − 3)2 − 16
√( 𝑥 − 3)2 = √ 𝑦 + 16
| 𝑥 − 3| = √ 𝑦 + 16
−𝑥 + 3 = √ 𝑦 + 16
𝑥 = 3 − √ 𝑦 + 16
𝑐𝑎𝑚𝑏𝑖𝑜 𝑑𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒
𝑦 = 3 − √ 𝑥 + 16
EJERCICIOS.-
1. Determinar los conjuntos A y B para que la función f sea biyectiva
𝑓: 𝐴 → 𝐵
𝑥 → 𝑓( 𝑥) = {
𝑥 + 2 𝑠𝑖 𝑥 < 0
𝑥2 − 9 𝑠𝑖 𝑥 ≥ 0
a) Demostrar si f es Inyectiva
b) En caso de no serlo, redefinir para que sea inyectiva
𝑓1 ( 𝑥) = 𝑥 + 2 𝑓2( 𝑥) = 𝑥2 − 9
𝑥 < 0 𝑥 ≥ 0
𝑓( 𝑥1) = 𝑓( 𝑥2) 𝑓( 𝑥1) = 𝑓( 𝑥2)
𝑥1 + 2 = 𝑥2 + 2 𝑥2
1 − 9 = 𝑥2
2 − 9
𝑥1 = 𝑥2 √𝑥2
1 = √𝑥2
2
𝑓1( 𝑥) 𝑒𝑠 𝑖𝑛𝑦𝑒𝑐𝑡𝑖𝑣𝑎 | 𝑥1| = | 𝑥2|
𝐷𝑓1: 𝑥 < 0 (+) (+)
𝑥 + 2 < 2 𝑥1 = 𝑥2
𝑅𝑓1: 𝑦 < 2 𝑓2( 𝑥) 𝑒𝑠 𝑖𝑛𝑦𝑒𝑐𝑡𝑖𝑣𝑎
𝐷𝑓2 : 𝑥 ≥ 0
𝑥2 ≥ 0
𝑥2 − 9 ≥ −9
𝑅𝑓2: 𝑦 ≥ −9
𝑥 − 3 - +
-∞ 3 ∞
𝑓−1:[ −16,+∞[ → ] − ∞,3]
𝑥 → 𝑓−1 = 3 − √𝑥 + 16
a) 𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑎) 𝑓−1( 𝑥) = 3 − √ 𝑥 + 16 𝑠𝑖 𝑥 ≥ −16

5. 𝑅𝑓1 ∩ 𝑅𝑓2 = ] − ∞,2[ ∪ [−9, +∞[
𝑅𝑓1 ∩ 𝑅𝑓2 ≠ ∅
∴ 𝑓 𝑛𝑜 𝑒𝑠 𝑖𝑛𝑦𝑒𝑐𝑡𝑖𝑣𝑎
Redefinimos Inyectivida
𝑓1( 𝑥) = 𝑥 + 2 𝑓2( 𝑥) = 𝑥2 − 9
Raíz Raíces
𝑦 = 𝑥 + 2 𝑦 = 𝑥2 − 9
0 = 𝑥 + 2 0 = 𝑥2 − 9
𝑥 = −2 𝑥 = 3 ∨ 𝑥 = −3 𝑥 ≥ 0
𝐷𝑓1: 𝑥 < −2 𝐷𝑓2: 𝑥 ≥ 3
𝑥 + 2 < 0 𝑥2 ≥ 9
𝑅𝑓1: 𝑦 < 0 𝑥2 − 9 ≥ 0
𝑅𝑓2 ∶ 𝑦 ≥ 0
𝑓: ] − ∞,−2[ ∪ [3,+∞[ → 𝑅
𝑥 → 𝑓( 𝑥) = {
𝑥 + 2 𝑠𝑖 𝑥 < −2
𝑥2 − 9 𝑠𝑖 𝑥 ≥ 3
∴ 𝑓 𝑒𝑠 𝑖𝑛𝑦𝑒𝑐𝑡𝑖𝑣𝑎
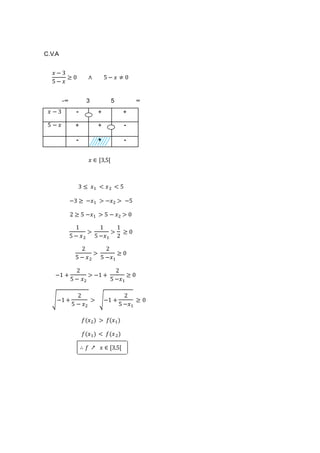
2. Sea 𝑓( 𝑥) = √
𝑥−3
5−𝑥
Analizar los intervalos de monotonía.
x – 3 - x + 5
-x + 5 -1
+ 2
2
-2 3
-∞ -9 2 ∞
𝑦 = √−1 +
2
5 − 𝑥

6. C.V.A
𝑥 − 3
5 − 𝑥
≥ 0 ∧ 5 − 𝑥 ≠ 0
-∞ 3 5 ∞
𝑥 − 3 - + +
5 − 𝑥 + + -
- + -
𝑥 ∈ [3,5[
3 ≤ 𝑥1 < 𝑥2 < 5
−3 ≥ −𝑥1 > −𝑥2 > −5
2 ≥ 5 −𝑥1 > 5 − 𝑥2 > 0
1
5 − 𝑥2
>
1
5 −𝑥1
>
1
2
≥ 0
2
5 − 𝑥2
>
2
5 −𝑥1
≥ 0
−1 +
2
5 − 𝑥2
> −1 +
2
5 −𝑥1
≥ 0
√−1 +
2
5 − 𝑥2
> √−1 +
2
5 −𝑥1
≥ 0
𝑓(𝑥2) > 𝑓(𝑥1)
𝑓(𝑥1) < 𝑓(𝑥2)
∴ 𝑓 ↗ 𝑥 ∈ [3,5[