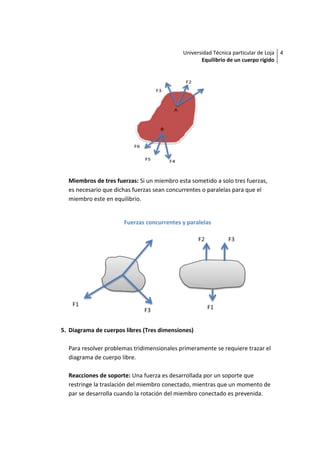
Este documento describe los conceptos fundamentales del equilibrio estático de cuerpos rígidos en dos y tres dimensiones. Explica que para que un cuerpo rígido esté en equilibrio, la suma de las fuerzas y la suma de los momentos de fuerza que actúan sobre él deben ser cero. Detalla cómo trazar diagramas de cuerpos libres y aplicar las ecuaciones de equilibrio escalares y vectoriales. También cubre temas como miembros de dos y tres fuerzas, restricciones de soporte, y ejercicios de aplicación

1. UNIVERSIDAD TÉCNICA PARTICULAR DE LOJA
Equilibrio de un cuerpo
rígido
Mecánica Racional
Stephanie Espinosa Torres
Diego González Freire
Rosalba Torres Bailón
Diego Valdivieso Eguiguren
07/11/2011
Ing. Carla Cartuche Carchi

2. Universidad Técnica particular de Loja 2
Equilibrio de un cuerpo rígido
Equilibrio de un Cuerpo Rígido
Por definición una partícula puede tener solo movimiento de traslación. Si la
resultante de las fuerzas que actúan sobre una partícula es cero, la partícula está
moviéndose con velocidad constante o está en reposo; en este último caso se
dice que está en equilibrio estático. Pero el movimiento de un cuerpo rígido en
general es de traslación y de rotación. En este caso, si la resultante tanto de las
fuerzas como de los torques que actúan sobre el cuerpo rígido es cero, este no
tendrá aceleración lineal ni aceleración angular, y si está en reposo, estará en
equilibrio estático. La rama de la mecánica que estudia el equilibrio estático de
los cuerpos se llama estática.
1. Condiciones para el equilibrio de un cuerpo rígido:
Primera Condición: La suma de las fuerzas aplicadas al cuerpo es cero.
ΣF = 0
F1 + F2 +….+ Fn = 0
Segunda Condición: Es la suma algebraica de los momentos con respecto a un
punto de las fuerzas aplicadas es igual a cero.
ΣM = 0
M 1 +M 2 +….+Mn = 0
2. Diagrama de Cuerpo Libre en dos dimensiones
La aplicación exitosa de las ecuaciones de equilibrio requiere de una
explicación completa de todas sus fuerzas externas conocidas y desconocidas

3. Universidad Técnica particular de Loja 3
Equilibrio de un cuerpo rígido
que actúan sobre el cuerpo. Una excelente manera de tomar todas estas
fuerzas es trazando el diagrama del cuerpo, o contorno del mismo.
Sobre dicho croquis es necesario apuntar todas las fuerzas y par de momentos
que se puedan ser considerar para aplicar las ecuaciones de equilibrio.
Reacciones en los soportes: se deben de considerar diversos tipos de
reacciones antes de empezar a trazar el diagrama.
Fuerzas externas e internas: Como cuerpo rígido esta compuesto por
partículas, pueden actuar sobre el tanto cargas externas como internas, al
trazar el diagrama no se incluyen dichas fuerzas externas.
Peso y centro de gravedad: Cuando el cuerpo esta expuesto a un campo
gravitatorio, cada partícula va a tener un peso especifico, al peso se lo
considera como una fuerza externa y su efecto indica como una sola fuerza
resultante actuando a través del centro de gravedad del cuerpo.
Modelos idealizados: Para efectuar un análisis de fuerzas correcto de
cualquier objeto, es importante considerar un modelo analítico o idealizado
de que sus resultados se aproximen tanto como sea posible a la situación real.
3. Ecuaciones de Equilibrio (dos dimensiones)
En esta sección solo necesitaremos dos ecuaciones indispensables para
obtener el equilibrio de un cuerpo rígido las que son: ∑Fx=0, ∑Fy=0 y ∑Mo=0.
Se suma las fuerzas a lo largo de un eje de manera que elimine tantas fuerzas
desconocidas como sea posible, também debemos sumar los momentos con
respecto a un punto O que pase por la línea acción de tantas fuerzas
desconocidas como sea posible.
4. Miembros de dos y tres fuerzas
La resolución de algunos problemas de equilibrio puede ser mas simplificada
cuando es posible reconocer los miembros que se les esta aplicando dos o tres
fuerzas:
Miembros de dos fuerzas: Es aquel que no está sometido a momentos de par
y se aplican fuerzas en sólo dos puntos sobre dicho miembro.

4. Universidad Técnica particular de Loja 4
Equilibrio de un cuerpo rígido
Miembros de tres fuerzas: Si un miembro esta sometido a solo tres fuerzas,
es necesario que dichas fuerzas sean concurrentes o paralelas para que el
miembro este en equilibrio.
Fuerzas concurrentes y paralelas
5. Diagrama de cuerpos libres (Tres dimensiones)
Para resolver problemas tridimensionales primeramente se requiere trazar el
diagrama de cuerpo libre.
Reacciones de soporte: Una fuerza es desarrollada por un soporte que
restringe la traslación del miembro conectado, mientras que un momento de
par se desarrolla cuando la rotación del miembro conectado es prevenida.

5. Universidad Técnica particular de Loja 5
Equilibrio de un cuerpo rígido
6. Ecuaciones de Equilibrio
Para lograr el equilibrio de un cuerpo rígido el cual esta sometido a un sistema
tridimensional de fuerza requieren que la fuerza resultante y el momento par
resultante que actúan sobre el cuerpo sean igual a cero.
Ecuaciones vectoriales de equilibrio: Las condiciones se las puede expresar en
forma vectorial: ∑F=0; ∑Mo=0, donde ∑F es la sumatoria de las fuerzas
externas y ∑Mo es la sumatoria de los momentos par y los momentos de
todas las fuerzas con respecto de O.
Ecuaciones escalares de equilibrio: Se las expresa en la forma vectorial
cartesiana como: ∑F=∑Fxi+∑Fyj+∑Fzk y ∑Mo=∑Mxi+∑Myj+∑Mzk .
7. Restricciones para un cuerpo rígido
Para asegurar el equilibrio de un cuerpo rígido no solo es necesario satisfacer
las ecuaciones, sino que el cuerpo esta sostenido o restringido por soportes;
en algunos cuerpos suelen tener mas que los necesarios y otros cuerpos no
tienen los soportes necesarios, existen dos casos:
Restricciones Redundantes: Cuando tiene soportes redundantes, es decir
más de los necesarios para mantenerlo en equilibrio se vuelve estáticamente
indeterminado (más cargas desconocidas).
Restricciones Impropias: En algunos casos puede haber tantas fuerzas
desconocidas sobre el cuerpo como ecuaciones de equilibrio; sin embargo
puede mostrar inestabilidad debido a las restricciones impropias de los
soportes.
8. Ejercicios de Aplicación
5-2 Trace el diagrama de cuerpo libre de la perforadora manual que está articulada en A
y se apoya sobre la superficie lisa en B.

6. Universidad Técnica particular de Loja 6
Equilibrio de un cuerpo rígido
5-12 Determine la magnitud de la fuerza resultante que actúa en el pasador A de
la perforadora en el problema anterior.
-8lb =0 8lb (1,5 pies) -
=0
= 8 lb = 6 lb
= = = 10 lb //Rta
5-32 El carro deportivo tiene masa de 1.5 Mg y centro de masa G. Si cada uno
de los dos resortes frontales tiene rigidez de = 58 kN/my los dos resortes
posteriores tiene rigidez de = 65 kN/m, determine sus compresiones
cuando el carro está estacionado sobre un camino de 30° de pendiente.
También ¿Qué fuerza de fricción debe ser aplicada a cada una de las
ruedas posteriores para mantener el carro en equilibrio?
Sugerencia: Determine primero la fuerza normal en A y B, y luego calcule
la compresión en los resortes.

7. Universidad Técnica particular de Loja 7
Equilibrio de un cuerpo rígido
14,7 N(cos 30°)( 1,2 ) – 14,7N(sen 30°)( 0,4 ) - 2 (2)=0
= 3284 N
2 – 14,7N ( sen 30°) = 0
= 3678 N
2 + 2(3087 N) – 14,7N (cos 30°) = 0
= 3284 N
Compresión en los resortes
X=
= = 53,2 mm//Rta
= = 50,5 mm//Rta
5-52 La viga rígida de peso insignificante está soportada horizontalmente
por dos resortes y un pasador. Si los resortes no están comprimidos
cuando se retire la carga. Determine la fuerza presente en cada resorte
cuando se aplica la carga P. Calcule también la deflexión vertical del

8. Universidad Técnica particular de Loja 8
Equilibrio de un cuerpo rígido
extremo C. Suponga que la rigidez k del resorte A es lo suficientemente
grande como para que se representen sólo deflexiones pequeñas.
9. Sugerencias: La viga gira con respecta a A y las deflexiones en los resortes
puedan estar relacionadas.