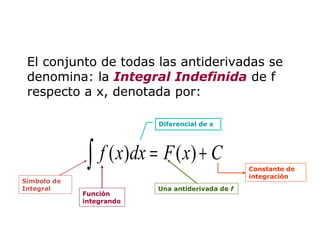
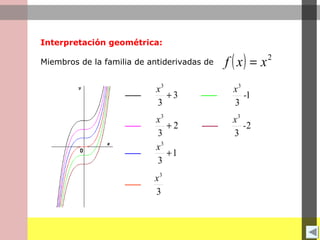
Este documento introduce el concepto de integral indefinida y cómo calcularla. Explica que la integral indefinida de una función es la antiderivada de esa función más una constante arbitraria C. Proporciona fórmulas para calcular la integral indefinida de funciones como potencias, exponenciales, seno y coseno. Finalmente, presenta propiedades clave de la integral indefinida como la linealidad y el cambio de variable constante.

1. UNIDAD 1
La Integral
“Nociones de Integrales”

2. En esta actividad aprenderás a:
 Interpretar
el
concepto
de
la
Integral.
 Calcular la integral de funciones
específicas.
 Utilizar el concepto de integral para
calcular áreas.

3. Integral indefinida
Lo opuesto a una derivada es una antiderivada o
integral indefinida.
La integral indefinida de una función f(x) se
denota como
Y está definida por la propiedad

4. La integral indefinida
• Si una función es diferenciable.
• Una función tiene un número infinito de
integrales, que difieren por una constante
aditiva.

5. La integral de una función
idénticamente cero.
La integral indefinida de una función cuya
derivada es idénticamente cero
donde C es una constante arbitraria.
La integral indefinida de una función idénticamente
cero es una constante

6. El conjunto de todas las antiderivadas se
denomina: la Integral Indefinida de f
respecto a x, denotada por:
Diferencial de x
∫
Símbolo de
Integral
f ( x)dx = F ( x) + C
Función
integrando
Una antiderivada de f
Constante de
integración

7. La integral indefinida de una constante.
La integral indefinida de la función constante:
Donde c es una constante.

8. La integral indefinida de la función identidad.
La integral indefinida de la función identidad:
Donde c es una constante arbitraria.

9. La integral indefinida de una potencia de x.
La integral indefinida de la función
Donde c es una constante arbitraria.
es:

10. La integral indefinida de una potencia de 1/x.
Para una función de la forma
Dado que
Entonces:

11. Interpretación geométrica:
Miembros de la familia de antiderivadas de
f ( x) = x
x3
+3
3
x
x3
-1
3
x3
+2
3
x3
+1
3
x3
-2
3
x3
3
2

12. EJEMPLOS
Encuentre la antiderivada más general de cada una
de las siguientes funciones.
a ) f(x) = 8x
3
b) f ( x) = e x
1
c) f(x) =
x
d ) f ( x) = cos x

13. EJEMPLOS
Determine:
a ) ∫ x dx
5
b) ∫ e dx
2x
c) ∫ sen(3 x)dx

14. PROPIEDADES DE LA INTEGRAL
INDEFINIDA
1. Del múltiplo constante:
kf ( x)dx = k ∫ f ( x)dx
∫
2. De la suma o diferencia:
∫ [ f ( x) ± g ( x)] dx = ∫ f ( x)dx ±∫ g ( x)dx
CUIDADO:
∫ f ( x) g ( x)dx ≠ ∫ f ( x)dx ∫ g ( x)dx

15. Fórmulas de integración
1.
x n +1
x n dx =
+C
∫
n +1
2.
x −1dx = ln x + C
∫
3.
e kx
kx
∫ e dx = k + C
Ejemplos
Ejemplos

16. Fórmulas de integración
4.
sen( kx)
∫ cos(kx)dx = k + C
5.
− cos( kx)
+C
∫ sen(kx)dx = k
6.
7.
tan(kx)
∫ sec (kx)dx = k + C
2
1
∫ 1 + x 2 dx = arctan( x) + C