Este documento describe la simulación de los métodos iterativos de Jacobi y Gauss-Seidel para resolver sistemas de ecuaciones lineales. Explica cómo funcionan los métodos, incluido el cálculo de iteraciones sucesivas hasta alcanzar un error menor a un umbral. También incluye código en Fortran que implementa los métodos y un ejemplo numérico para ilustrarlos.

1. SIMULACIÓN DE YACIMIENTOS
TAREA I: SIMULACIÓN EN FORTRAN DEL MÉTODO ITERATIVO DE JACOBI Y GAUSS SEIDEL.
José Alejandro Lozano Arias
Juan David Vallejo Restrepo
1. Método de Jacobi
¿En qué consiste el método?
El método de Jacobi plantea una solución numérica 𝑋𝑖
(𝑘)
, al sistema de ecuaciones lineales 𝐴𝑥 = 𝑏,
cabe resaltar que la matriz 𝐴 debe ser diagonalmente dominante para que exista una solución del
sistema. Matemáticamente los 𝑋𝑖
(𝑘)
se hallan con la siguiente formula:
𝑋𝑖
(𝑘)
=
(𝑏𝑖 − ∑ 𝑎𝑖𝑗 𝑥𝑗
(𝑘−1)𝑛
𝑗=1,𝑗≠1 )
𝑎𝑖𝑖
(1)
Operativamente el proceso empieza asignando valores iniciales a las variables, de tal forma que
para la próxima iteración se sustituyen los valores obtenidos de las variables en la iteración
inmediatamente anterior.
El método para determinar que la aproximación es buena es por medio del criterio del residuo.
 1
0
m
i ij j
reli
Max
b A X
Res
Res




(2)

2. Código en fortran para el método de Jacobi

3. ¿Qué hace el código?
- Para comenzar, se declaran las variables necesarias que se utilizarán en todo el programa,
también el vector A, B, Xo (vector de aproximación inicial), Xk (vector solución) y mult, que
es un vector que guarda el producto de matriz por vector.
- Después el programa pide al usuario que digite la dimensión de la matriz A y de acuerdo a
éste, redefine las dimensiones de los matrices y los vectores que usará en adelante.

4. - A continuación el programa lee de un archivo .txt (que debe estar ubicado en la misma
carpeta del ejecutable ‘Jacobi’), los valores de la matriz A, del vector B y del vector Xo. A su
vez, el usuario debe ingresar el error que desea utilizar para el criterio de convergencia y un
número máximo de iteraciones a realizar.
- El programa toma el vector inicial Xo, y le aplica el método de Jacobi haciendo la primera
iteración.
- Como el criterio de convergencia es B-AX<Tol, es necesario calcular el producto de la matriz
A, por el vector X encontrado en la iteración anterior. Se usó un ciclo para encontrar A(X) y
a ese resultado se le llamó mult.
- El error se calculará por medio de la norma infinito de B-AX, la cual toma el mayor valor del
vector, que para ésta primera iteración será el residuo inicial.
- Se inicializa un contador llamado L, que llevará registro de las iteraciones que se han
realizado (L va hasta el valor que haya ingresado el usuario) y aplica el método de Jacobi
para el nuevo vector Xo.
- Calcula nuevamente B-AX, con el vector obtenido en la iteración anterior.
- A continuación se calcula la norma infinito de B-AX, ésta se divide entre el residuo inicial y
se compara con el error que el usuario definió.
- Finalmente, si el error relativo es menor que el error que el usuario ingresó, el programa se
detiene e imprime el valor final de Xk y L, que es la cantidad de iteraciones que hizo. De lo
contrario, vuelve a definir Xo igual a Xk y vuelve a empezar el ciclo.
2. Método de Gauss Seidel
¿En qué consiste el método?
Éste método emplea valores iniciales y posteriormente itera para obtener mejores aproximaciones
a la solución. Es especialmente adecuado cuando se tiene un gran número de ecuaciones. Dado que
el error en éste método viene dado por el número de iteraciones, el error de redondeo no suele
preocupar.
El método de Gauss Seidel supone un sistema de n ecuaciones:
[𝐴]{𝑋} = {𝐵} (3)
Y calcula los valores de 𝑋𝑖 como:
𝑋𝑖 =
𝑏𝑖 − ∑ 𝑎𝑖𝑗 𝑥𝑗 − ∑ 𝑎𝑖𝑗 𝑋𝑂𝑗
𝑛
𝑗=1
𝑖−1
𝑗=1
𝑎𝑖𝑖
(4)
Se empieza el proceso de solución escogiendo valores iniciales para las x. Éstos valores se sustituyen
en la ecuación 3, la cual se utiliza para calcular un nuevo valor de 𝑋𝑖. Después se reemplaza el nuevo
valor de 𝑋𝑖 en la ecuación 3 y se calcula el nuevo valor de 𝑋2, y de la misma forma se hace hasta
calcular el último valor del sistema que corresponde a 𝑋 𝑛. Después se regresa a la primera ecuación
y se repite todo el procedimiento hasta que el error sea menor a una tolerancia fijada.

5. La calidad de la aproximación se mide usando el criterio del residuo.
 1
0
m
i ij j
reli
Max
b A X
Res
Res




(5)
A primera vista, el método iterativo de Jacobi y el de Gauss Seidel son muy similares, sin embargo,
dichos métodos varían con respecto a la asignación de los datos de las variables para la iteración 2
en adelante; es decir, en el método de Jacobi el valor que se tiene después de la iteración es el que
se asignará a la nueva variable, mientras que en el método de Gauss Seidel, los valores que se van
obteniendo de la variable se van reemplazando de manera sucesiva en las otras ecuaciones.
A continuación se muestra un esquema comparativo entre Gauss Seidel (a) y Jacobi (b), para un
supuesto de una matriz 3X3
Ilustración 1. Diferencia entre los métodos de a) Gauss Seidel y b) Jacobi, para un sistema de ecuaciones lineales 3X3.
Tomado de [1]

6. Código en fortran para Gauss Seidel

7. ¿Qué hace el código?
- Para comenzar, se declaran las variables necesarias que se utilizarán en todo el programa,
también el vector A, B, Xo (vector de aproximación inicial), Xk (vector solución) y mult, que
es un vector que guarda el producto de matriz por vector.
- Después el programa pide al usuario que digite la dimensión de la matriz A y de acuerdo a
éste, redefine las dimensiones de los matrices y los vectores que usará en adelante.
- A continuación el programa lee de un archivo .txt (que debe estar ubicado en la misma
carpeta del ejecutable ‘Gauss Seidel’), los valores de la matriz A, del vector B y del vector
Xo. A su vez, el usuario debe ingresar el error que desea utilizar para el criterio de
convergencia y un número máximo de iteraciones a realizar.
- El programa toma el vector inicial Xo, y le aplica el método de Gauss Seidel haciendo la
primera iteración
- Como el criterio de convergencia es B-AX<Tol, es necesario calcular el producto de la matriz
A, por el vector X encontrado en la iteración anterior. Se usó un ciclo para encontrar A(X) y
a ese resultado se le llamó mult.
- El error se calculará por medio de la norma infinito de B-AX, la cual toma el mayor valor del
vector, que para ésta primera iteración será el residuo inicial.
- Se inicializa un contador llamado L, que llevará registro de las iteraciones que se han
realizado (L va hasta el valor que haya ingresado el usuario) y aplica el método de Gauss
Seidel para el nuevo vector Xo.
- Calcula nuevamente B-AX, con el vector obtenido en la iteración anterior.
- A continuación se calcula la norma infinito de B-AX, ésta se divide entre el residuo inicial y
se compara con el error que el usuario definió.
- Finalmente, si el error relativo es menor que el error que el usuario ingresó, el programa
para e imprime el valor final de Xk y L, que es la cantidad de iteraciones que hizo. De lo
contrario, vuelve a definir Xo igual a Xk y vuelve a empezar el ciclo.

8. Ejemplo de aplicación
Se creó una matriz 4x4, sabiendo de antemano que las soluciones son 𝑋1 = 1, 𝑋2 = 2, 𝑋3 = −1,
𝑋4 = 1 así:
{
10𝑋1 − 𝑋2 + 2𝑋3 = 6
−𝑋1 + 11𝑋2 − 𝑋3 + 3𝑋4 = 25
2𝑋1 − 𝑋2 + 10𝑋3 − 𝑋4 = −11
3𝑋2 − 𝑋3 + 8𝑋4 = 15
Y con base en lo anterior, se corre ésta misma matriz en el simulador aplicando los métodos de
Jacobi y Gauss Seidel. Los resultados obtenidos, junto con el número de iteraciones son:
Procedimiento usando Jacobi y el código en Fortran
Ilustración 2. Captura de pantalla, resultados Método Jacobi en Fortran
Se puede observar que el simulador después de ingresar la dimensión de la matriz y tomar los datos
del .txt, realiza 9 iteraciones (de acuerdo a la tolerancia que se le fijó) y arroja como resultado: X1=
0.99967, X2= 2.00044, X3= -1.00036, X4= 1.00061; que prácticamente no difieren de la solución real
que es 𝑋1 = 1, 𝑋2 = 2, 𝑋3 = −1, 𝑋4 = 1.

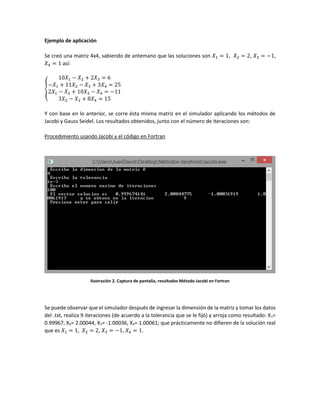
9. Procedimiento usando Jacobi y el código en Fortran
Ilustración 3. Captura de pantalla, resultados Método de Gauss Seidel en Fortran
Se puede observar que el simulador después de ingresar la dimensión de la matriz y tomar los datos
del .txt, realiza 5 iteraciones (de acuerdo a la tolerancia que se le fijó) y arroja como resultado: X1=
0.99938, X2= 1.99982, X3= -0.99978, X4= 1.00009; que prácticamente no difieren de la solución real
que es 𝑋1 = 1, 𝑋2 = 2, 𝑋3 = −1, 𝑋4 = 1.
En definitiva ambos métodos manejan una alta precisión y demuestran efectividad para la solución
de sistemas de ecuaciones lineales nxn.
Referencias
[1] D. López y Y. Ceballos, Método de Jacobi, Medellín.
[2] S. Chapra y R. Canale, Métodos Numéricos para Ingenieros, McGraw-Hill, 2006.