Este documento introduce los conceptos de integrales múltiples. Explica cómo se calcula el volumen de un prisma rectangular limitado por una función de dos variables mediante una integral doble. Luego define la integral doble sobre un rectángulo y sus propiedades, y cómo se puede calcular la integral doble sobre regiones más generales. Finalmente, introduce brevemente los conceptos de integral triple y cambio de variables en integrales dobles.

1. Tema 4
Integrales m´ultiples
4.1 Introducci´on.
En el primer curso de Fundamentos se plante´o el problema de hallar el ´area comprendida
entre la gr´afica de una funci´on positiva y = f(x) , el eje OX y las rectas x = a, x = b.
Dicha ´area se representaba como b
a f(x)dx.
1

2. TEMA 4. INTEGRALES M ´ULTIPLES 2
Vimos que este problema estaba relacionado con el c´alculo de una primitiva de f(x) .
El Teorema de Barrow nos asegura que si F(x) es tal que F (x) = f(x) entonces
A = b
a f(x)dx = F(b) − F(a).
Nuestro problema es el c´alculo del volumen de un prisma de base rectangular
R = [a, b] × [c, d] y limitado superiormente por la gr´afica de una funci´on z = f(x, y)
positiva.
A este volumen lo denotaremos por R f(x, y)dxdy.
Difiere del problema anterior en que no se resuelve encontrando una primitiva de
f(x, y) (no tiene sentido), sino por el c´alculo de vol´umenes por secciones.
El volumen vendr´a dado por la suma infinita de las ´areas de las secciones que se
obtienen al cortar el cuerpo por planos paralelos al plano XZ, o tambi´en sumando las
´areas de las infinitas secciones que se obtienen al cortar el cuerpo por planos paralelos al
plano Y Z.

3. TEMA 4. INTEGRALES M ´ULTIPLES 3
V =
R
f(x, y)dxdy =
d
c
A(y)dy =
b
a
A(x)dx
donde A(y) = b
a f(x, y)dx, A(x) = d
c f(x, y)dy considerando en cada caso la x o la y
fija.
As´ı V = d
c ( b
a f(x, y)dx)dy = b
a ( d
c f(x, y)dy)dx .
El problema se convierte en el c´alculo de una integral reiterada que ya sabemos resolver.
4.2 Integral doble sobre un rect´angulo.
Definamos ahora el concepto de integral doble de una funci´on z = f(x, y) no necesaria-
mente positiva sobre un rect´angulo R = [a, b] × [c, d].
Dividimos el intervalo [a, b] en n partes iguales, eligiendo para ello n + 1 puntos a =
x0 < x1 < x2 < · · · < xn = b siendo xi+1 − xi =
b − a
n
= ∆x.
Elegimos, de forma an´aloga, m + 1 puntos del intervalo [c, d]
c = y0 < y1 < y2 < · · · < ym = d con yi+1 − yi =
d − c
m
= ∆y.
As´ı obtenemos n · m rect´angulos [xi, xi+1] × [yj, yj+1] = Rij de ´area ∆A = ∆x · ∆y.
Sea cij = (x∗
i , y∗
j ) ∈ Rij ⇒ f(cij) · ∆A es el volumen del peque˜no prisma del dibujo.

4. TEMA 4. INTEGRALES M ´ULTIPLES 4
Llamemos
Snm =
n−1
i=0
m−1
j=0
f(cij)∆x∆y
Definici´on 4.1 (Integral doble)
Si existe lim
n,m→∞
Snm y no depende de la elecci´on de los valores cij, entonces se dice
que f es integrable sobre R y al valor de dicho l´ımite se le llama integral doble de f(x,y)
sobre R.
R
f(x, y)dxdy = limn,m→∞
n−1
i=0
m−1
j=0
f(cij)∆x∆y
Si f(x, y) es una funci´on positiva, R f(x, y)dxdy representa el volumen del prisma
rectangular de base R y limitado superiormente por la gr´afica de f.
Si f(x, y) es negativo, representa un volumen negativo.
Teorema 4.1 Cualquier funci´on continua sobre un rect´angulo es integrable.

5. TEMA 4. INTEGRALES M ´ULTIPLES 5
4.2.1 Propiedades de la integral doble.
I Linealidad. R[af(x, y) + bg(x, y)]dxdy = a R f(x, y)dxdy + b R g(x, y)dxdy.
II Monoton´ıa. Si f(x, y) ≥ g(x, y) ∀ (x, y) ∈ R , entonces :
R
f(x, y)dxdy ≥
R
g(x, y)dxdy
III Aditividad. Si D = R1 ∪ R2 es uni´on de dos rect´angulos disjuntos:
D f(x, y)dxdy = R1
f(x, y)dxdy + R2
f(x, y)dxdy
IV Teorema de Fubini. Si z = f(x, y) es continua sobre R = [a, b]×[c, d], entonces:
R
f(x, y)dxdy =
b
a
(
d
c
f(x, y)dy)dx =
d
c
(
b
a
f(x, y)dx)dy
4.3 Integral doble sobre regiones m´as generales.
Vamos a definir la integral doble de funciones sobre los siguientes tipos de regiones:
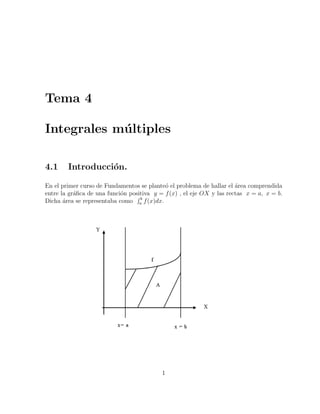
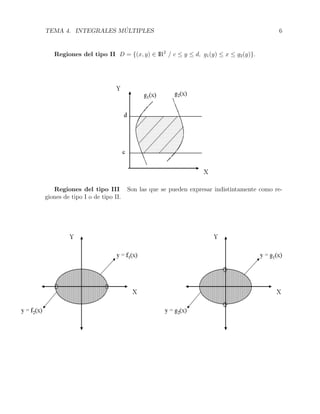
Regiones del tipo I D = {(x, y) ∈ IR2
/ a ≤ x ≤ b, f1(x) ≤ y ≤ f2(x)}.

6. TEMA 4. INTEGRALES M ´ULTIPLES 6
Regiones del tipo II D = {(x, y) ∈ IR2
/ c ≤ y ≤ d, g1(y) ≤ x ≤ g2(y)}.
Regiones del tipo III Son las que se pueden expresar indistintamente como re-
giones de tipo I o de tipo II.

7. TEMA 4. INTEGRALES M ´ULTIPLES 7
Definici´on 4.2 Sea D un regi´on de tipo I, II ´o III. Sea z= f(x,y) una funci´on continua.
Consideremos una regi´on de tipo I. Entonces:
D f(x, y)dxdy = b
a (
f2(x)
f1(x) f(x, y)dy)dx.
An´alogamente, en una regi´on de tipo II, se tiene:
D f(x, y)dxdy = d
c (
g2(y)
g1(y) f(x, y)dx)dy.

8. TEMA 4. INTEGRALES M ´ULTIPLES 8
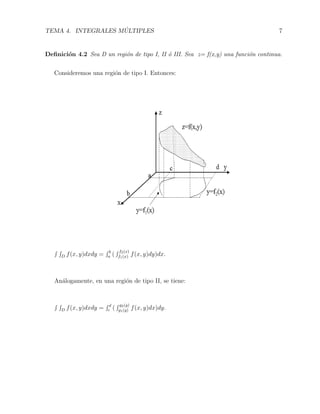
Para las regiones del tipo III, se puede calcular la integral doble de f(x, y) indistinta-
mente como una regi´on del tipo I ´o II. A veces la integral se complica y hay que elegir la
forma adecuada.
Consecuencia: Si D es una regi´on acotada de IR2
, entonces el volumen del prisma de
base D y altura 1 es: D dxdy = [la funci´on a integrar esf(x, y) = 1] = A(D)
Ejercicio Resuelve la integral doble
D
exp(y2
)dydx
donde D = {(x, y) ∈ IR2
/ 0 ≤ x ≤ 1, x ≤ y ≤ 1}.
Solucion:
1
0
(
1
x
exp(y2
)dy)dx =
1
0
(
y
0
exp(y2
)dx)dy =
1
2
(e − 1)

9. TEMA 4. INTEGRALES M ´ULTIPLES 9
4.4 Integral triple.
En el caso de las integrales triples se siguen los mismos pasos que en las integrales dobles.
Sea el paralelep´ıpedo R = [a, b] × [c, d] × [e, f]. Sea f(x, y, z) una funci´on continua
sobre R.
Definimos Sn,m,p =
n−1
i=0
m−1
j=0
p−1
k=0
f(cijk)∆x∆y∆z
donde xi+1 − xi =
b − a
n
= ∆x; yj+1 − yj =
d − c
m
= ∆y; zk+1 − zk =
f − e
p
= ∆z.
cijk = (x∗
i , y∗
j , z∗
k) con x∗
i ∈ [xi, xi+1], y∗
j ∈ [yj, yj+1], z∗
k ∈ [zk, zk+1]..
Definici´on 4.3 (Integral triple)
Si f es una funci´on acotada y, existe el lim
n,m,p→∞
Sn,m,p y no depende de la elecci´on de
los cijk, entonces se dice que f es integrable, y al valor de este l´ımite se le llama integral
triple sobre R, y se representa
R
f(x, y, z)dxdydz
• Consecuencia: Si f(x, y, z) = 1, entonces R f(x, y, z)dxdydz = V representa el
volumen.

10. TEMA 4. INTEGRALES M ´ULTIPLES 10
4.4.1 Propiedades.
Se cumplen las mismas propiedades que en la integral doble.
1. Toda funci´on continua es integrable
2. Linealidad, monoton´ıa y aditividad
3. Teorema de Fubini para integrales triples por el cual toda integral triple se puede
hallar por integraci´on reiterada.
4.5 Integrales triples sobre regiones m´as generales.
Se repite el mismo proceso que en las integrales dobles. Se consideran los siguientes tipos
de regiones:
Tipo I: a ≤ x ≤ b, f1(x) ≤ y ≤ f2(x), g1(x, y) ≤ z ≤ g2(x, y) (paralelep´ıpedo con
paredes frontal y posterior rectas).
W f(x, y, z)dxdydz = b
a (
f2(x)
f1(x) (
g2(x,y)
g1(x,y) f(x, y, z)dz)dy)dx.
Las regiones del tipo II son aquellas en las que c ≤ y ≤ d, (paralelep´ıpedos con
paredes izquierda y derecha planas).
Las regiones del tipo III son aquellas en las que e ≤ z ≤ f, (paralelep´ıpedos con
fondo y tapa planas).
Sus integrales triples se resuelven de manera an´aloga.
Las regiones del tipo IV son aquellas que se pueden expresar indistintamente como
regiones de los tipos I, II o III.
• Consecuencia: Si f(x, y, z) = 1 y W es una regi´on acotada de IR3
, entonces:
W dxdydz = vol(W)

11. TEMA 4. INTEGRALES M ´ULTIPLES 11
4.6 Cambio de variables en integrales dobles.
Una de las t´ecnicas m´as usuales en el c´alculo de integrales es el cambio de variables, cuyo
objetivo es transformar la integral a calcular en otra ”m´as sencilla”.
Esta t´ecnica ya fue estudiada para funciones de una variable, y el objetivo de este
ep´ıgrafe es hacerlo para funciones de dos variables.
En el c´alculo de una variable, cuando ten´ıamos una integral definida b
a f(x)dx , al
hacer un cambio de variables x = g(t), quedaban afectados el integrando, el intervalo de
integraci´on y el dx.
El nuevo integrando ser´ıa f(g(t)) (hay que exigir que Im(g) ⊂ D(f)).
Para calcular el nuevo intervalo de integraci´on necesitamos exigir que g poseea funci´on
inversa.
Si x = g(t) ⇒ t = g−1
(x) luego si x ∈ [a, b] ⇒ t ∈ g−1
([a, b]). Sea [t0, t1] =
g−1
([a, b]) el nuevo intervalo de integraci´on. Para que g posea funci´on inversa basta exigir
que g sea continua e inyectiva.
Adem´as como dx = g (t)dt entonces g debe ser derivable.
Veamos qu´e sucede en una integral doble.
Dada D f(x, y)dxdy , queremos hacer el cambio de variables: (x, y) = T(u, v)
T : D∗
⊂ IR2
−→ D ⊂ IR2
.
En el integrando no hay problemas, el nuevo integrando ser´a f ◦ T(u, v) .
La nueva regi´on D∗
debe cumplir que D = T(D∗
) ⇒ D∗
= T−1
(D) ⇒ T debe
ser inyectiva.
¿ Qu´e ocurre con dxdy?
D f(x, y)dxdy = lim
n,m→∞
n−1
i=0
m−1
j=0
f(cij)∆x∆y.
dxdy proviene de tomar l´ımite en ∆x∆y , ´area del rect´angulo. dxdy representa el
´area del rect´angulo infinitesimal y se le denomina elemento de ´area.
Nos preguntamos: ¿ En qu´e se transforma un elemento de ´area mediante la transfor-
maci´on T?

12. TEMA 4. INTEGRALES M ´ULTIPLES 12
Sabemos que T((u0, v0) + (∆u, ∆v)) ∼= T(u0, v0) + DT(u0, v0) ·
∆u
∆v
=
= T(u0, v0) +






∂T1
∂u
(u0, v0)
∂T1
∂v
(u0, v0)
∂T2
∂u
(u0, v0)
∂T2
∂v
(u0, v0)






∆u
∆v
= (x0, y0) + (Tu∆u + Tv∆v).
Sabemos que el ´area de un paralelogramo en IR3
cuyos lados son los vectores
a y b es a ∧ b .
Un paralelogramo en IR2
cuyos lados sean (a, b), (c, d) se pueden considerar como
vectores de IR3
(a, b, 0), (c, d, 0) con lo que el ´area ser´a (a, b, 0) ∧ (c, d, 0) = |ad − bc|
(donde | · | representa el valor absoluto).
Luego A(R) = ∆u∆v ⇒ ´Area(T(R)) ∼= (´Area del paralelogramo cuyos lados son
Tu∆u, Tv∆v) =
∂T1
∂u
∆u
∂T1
∂v
∆v
∂T2
∂u
∆u
∂T2
∂v
∆v
=
∂T1
∂u
∂T1
∂v
∂T2
∂u
∂T2
∂v
∆u∆v
con valor absoluto =
∂(x, y)
∂(u, v)
∆u∆v.
Teorema 4.2 (Teorema del cambio de variable para integrales dobles)
Sean D y D∗
regiones elementales de IR2
. Sea T : D∗
−→ D una funci´on de clase
C1
e inyectiva. Entonces, para cualquier funci´on f : D −→ IR integrable
D
f(x, y)dxdy =
D∗
f(T(u, v)) ·
∂(x, y)
∂(u, v)
dudv
Nota A veces, como ocurre en el caso de cambio a coordenadas polares, el cambio
no es inyectivo en todo el dominio. El teorema tambi´en se verifica en situaciones de este
tipo, siempre que el conjunto de puntos donde no se verifique sea la frontera del dominio,
o un subconjunto de ella.
4.7 Cambio de variables en integrales triples.
Es parecido al cambio de variables en integrales dobles.

13. TEMA 4. INTEGRALES M ´ULTIPLES 13
W f(x, y, z)dxdydz y sea T : IR3
−→ IR3
(x, y, z) = T(u, v, w).
A dxdydz se le llama elemento de volumen. Representa el volumen de un para-
lelep´ıpedo infinitesimal dxdydz = dV .
Sabemos que el volumen de un paralelep´ıpedo en IR3
cuyos vectores son a =
(a1, a2, a3), b = (b1, b2, b3) y c = (c1, c2, c3) se obtiene por el producto mixto.
V = a · (b ∧ c) =
a1 a2 a3
b1 b2 b3
c1 c2 c3
en valor absoluto.
Por consideraciones an´alogas a las que hicimos para integrales dobles, el elemento de
volumen dV = dxdydz , resultado de transformar mediante T el elemento de volumen
dudvdw es:
dxdydz =
∂(x, y, z)
∂(u, v, w)
dudvdw
Podemos, pues, enunciar el siguiente resultado:
Teorema 4.3 (Teorema del cambio de variable para integrales triples)
Sean W y W∗
regiones elementales de IR3
. Sea T : W∗
−→ W una funci´on de clase
C1
e inyectiva (salvo, quiz´as, en la frontera ∂W∗
). Entonces, para cualquier funci´on
f : W −→ IR integrable
W
f(x, y, z)dxdydz =
W∗
f(T(u, v, w)) ·
∂(x, y, z)
∂(u, v, w)
dudvdw
Ejercicio Calcular los elementos de volumen que resultan al aplicar el cambio a
coordenadas cil´ındricas y a coordenadas esf´ericas.