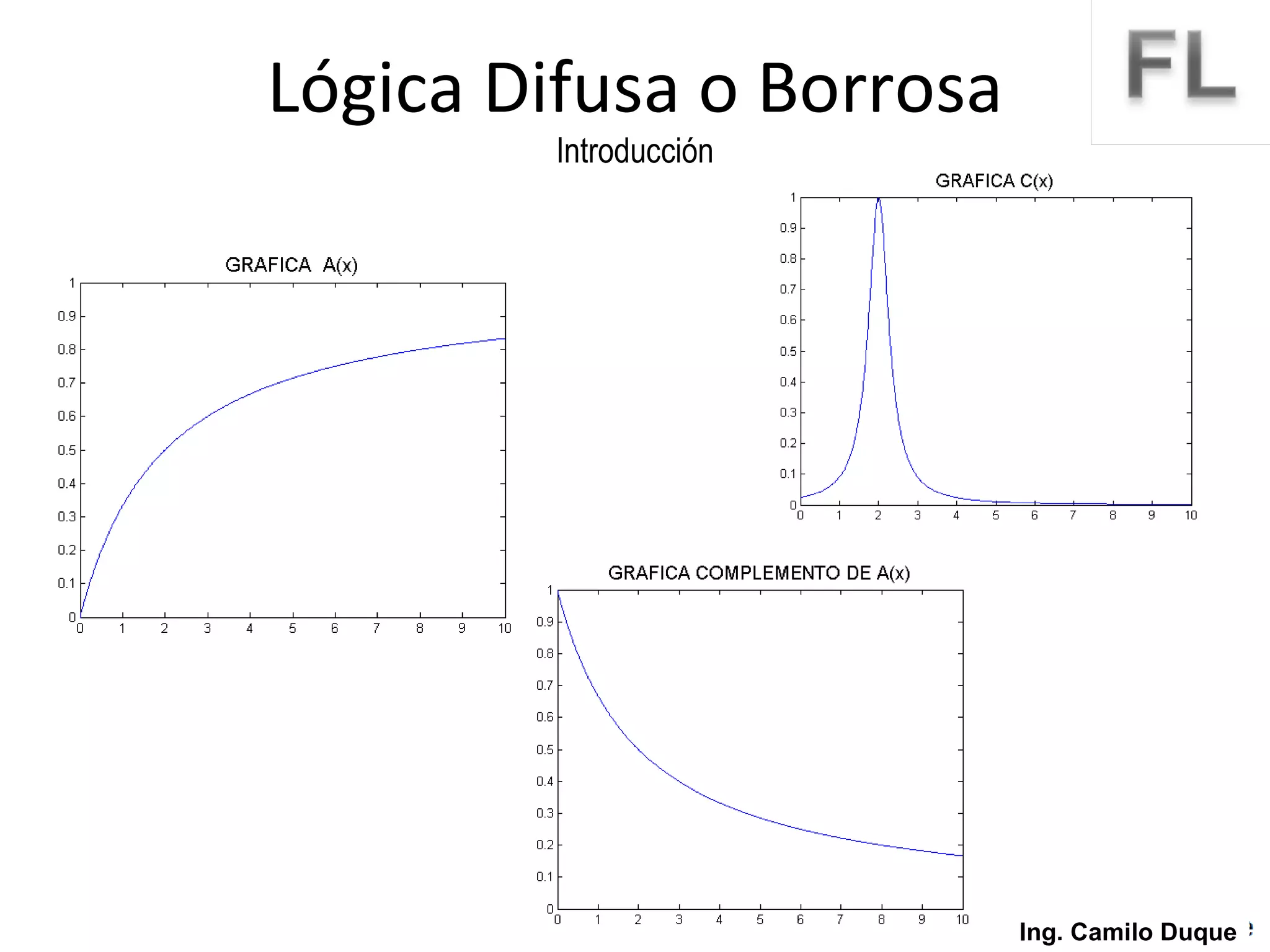
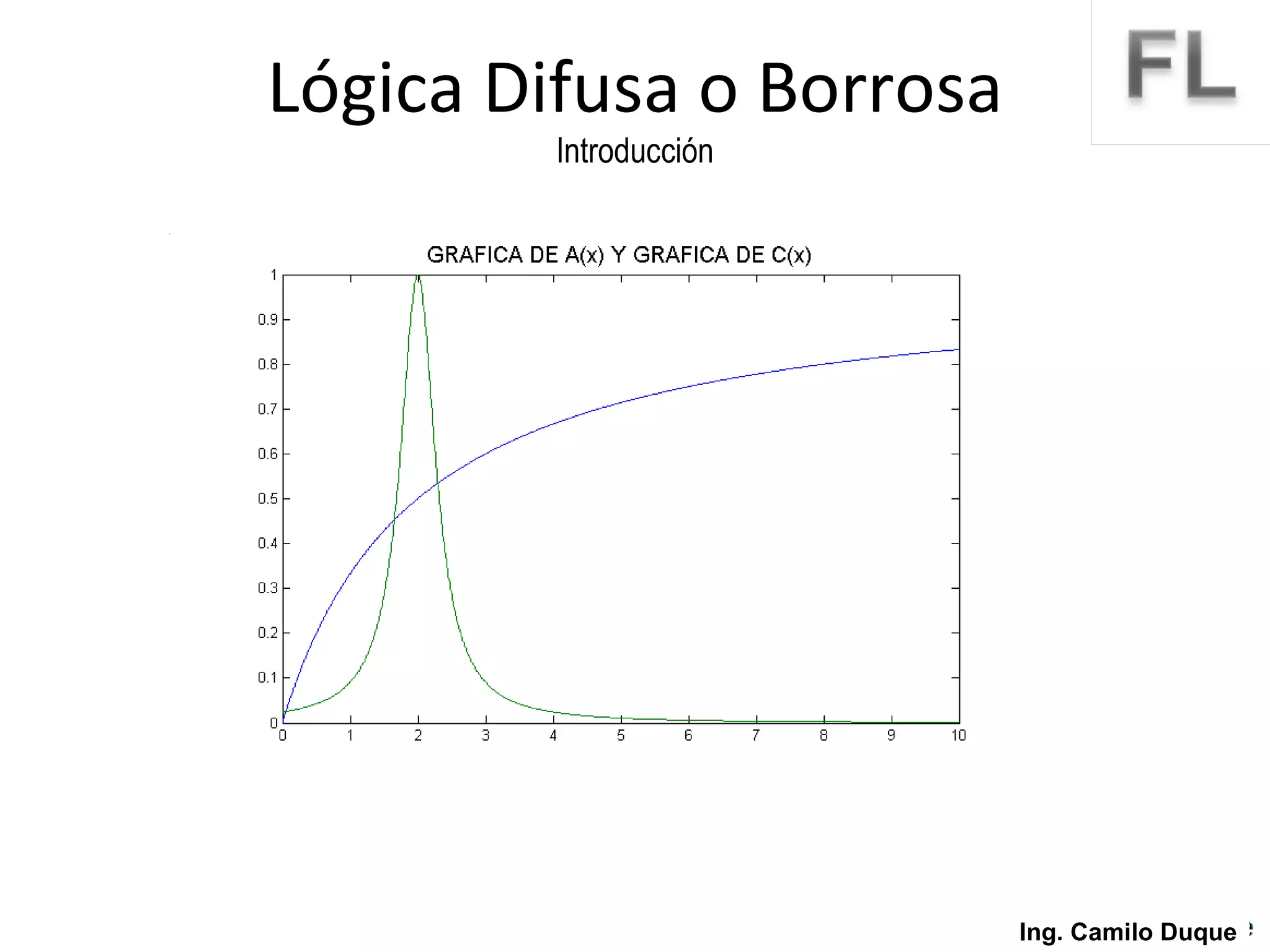
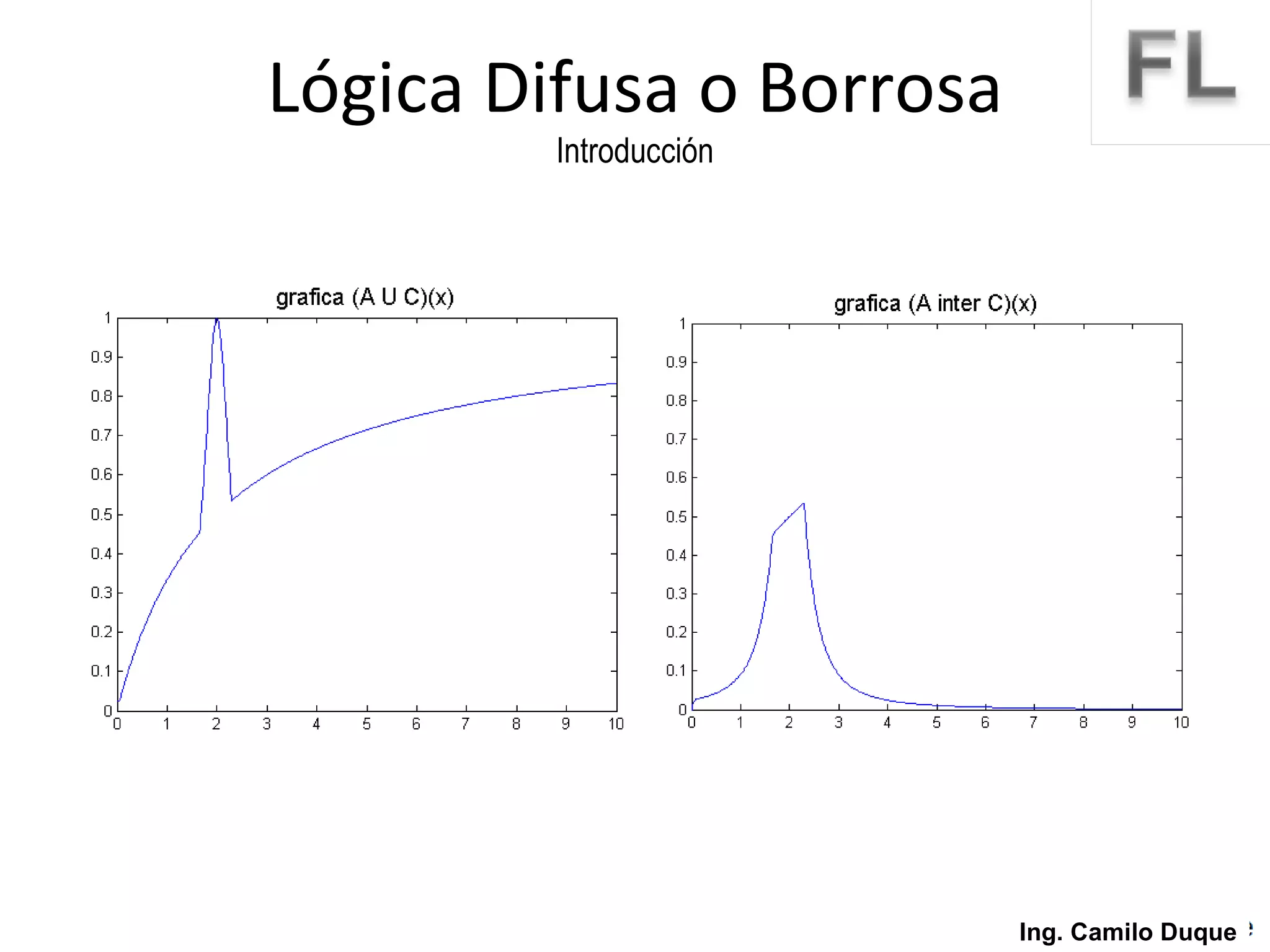
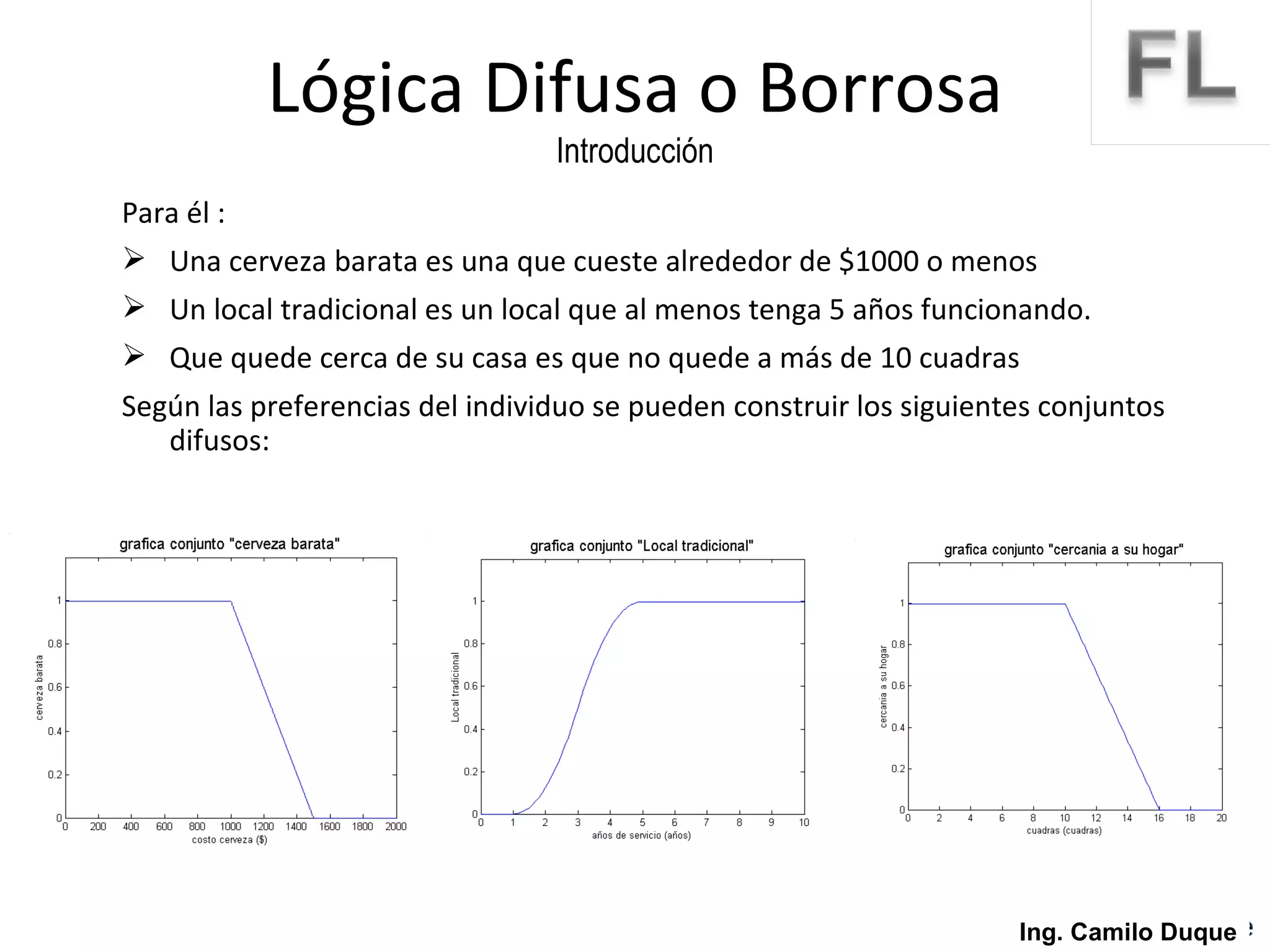
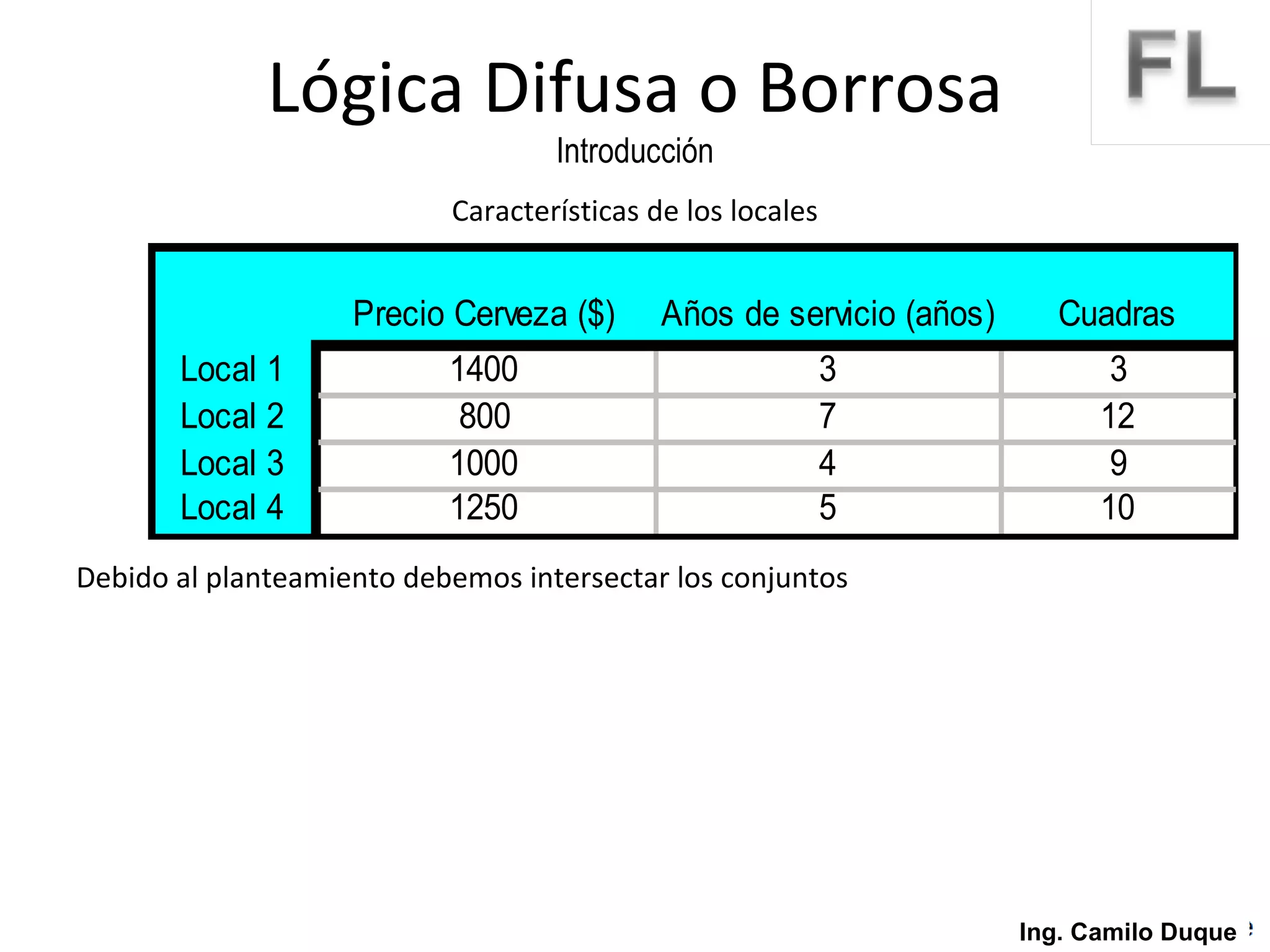
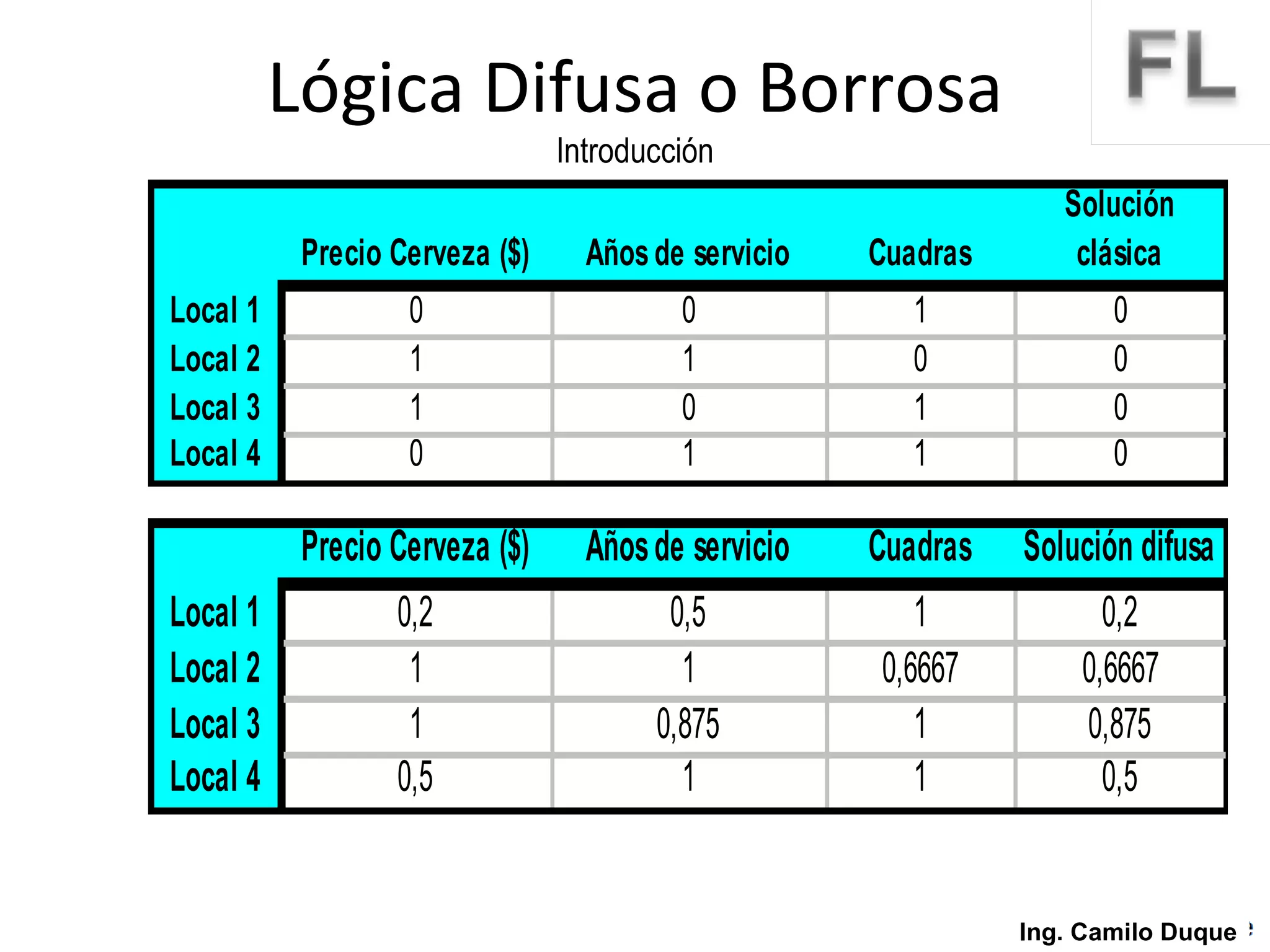
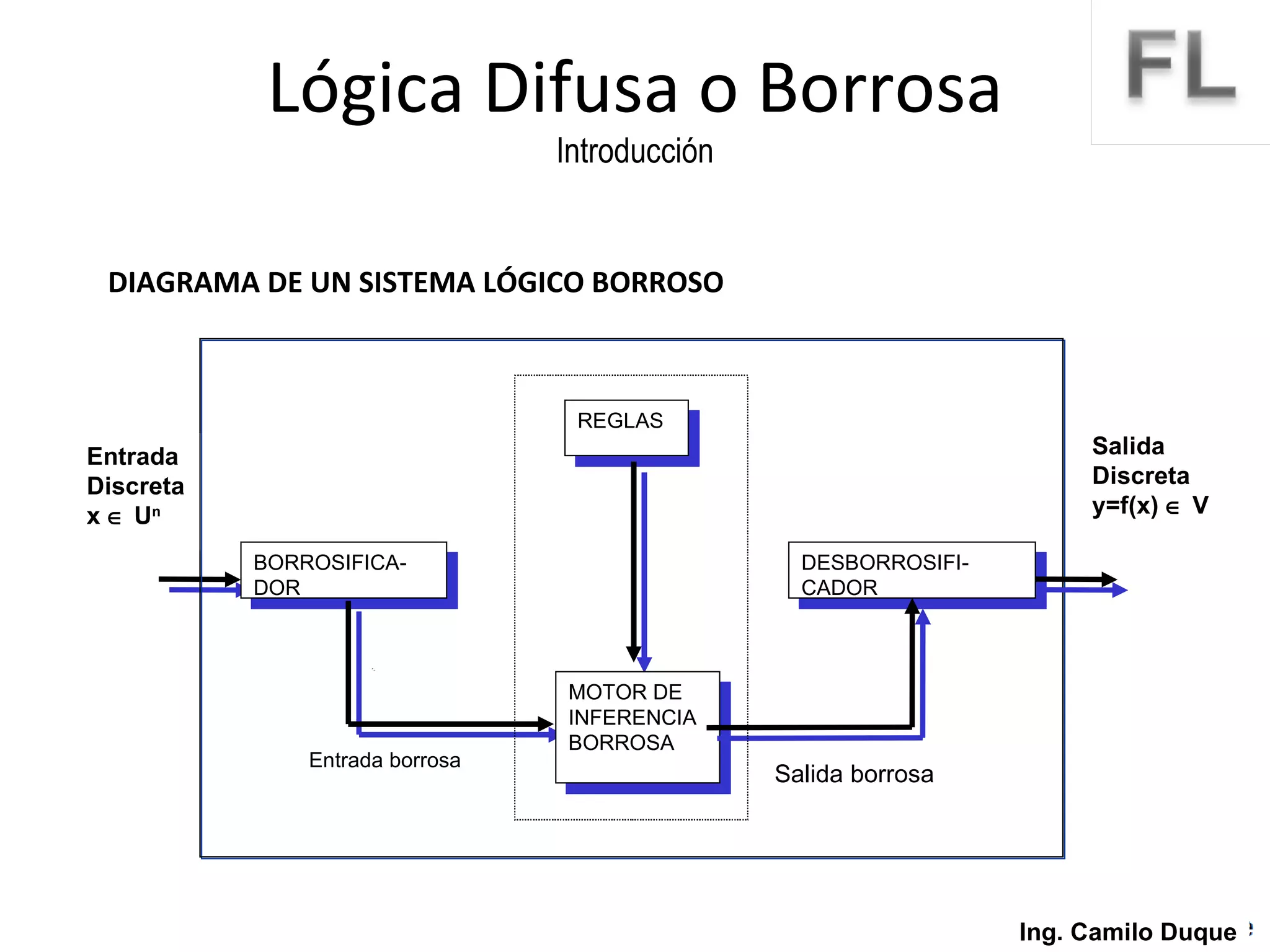
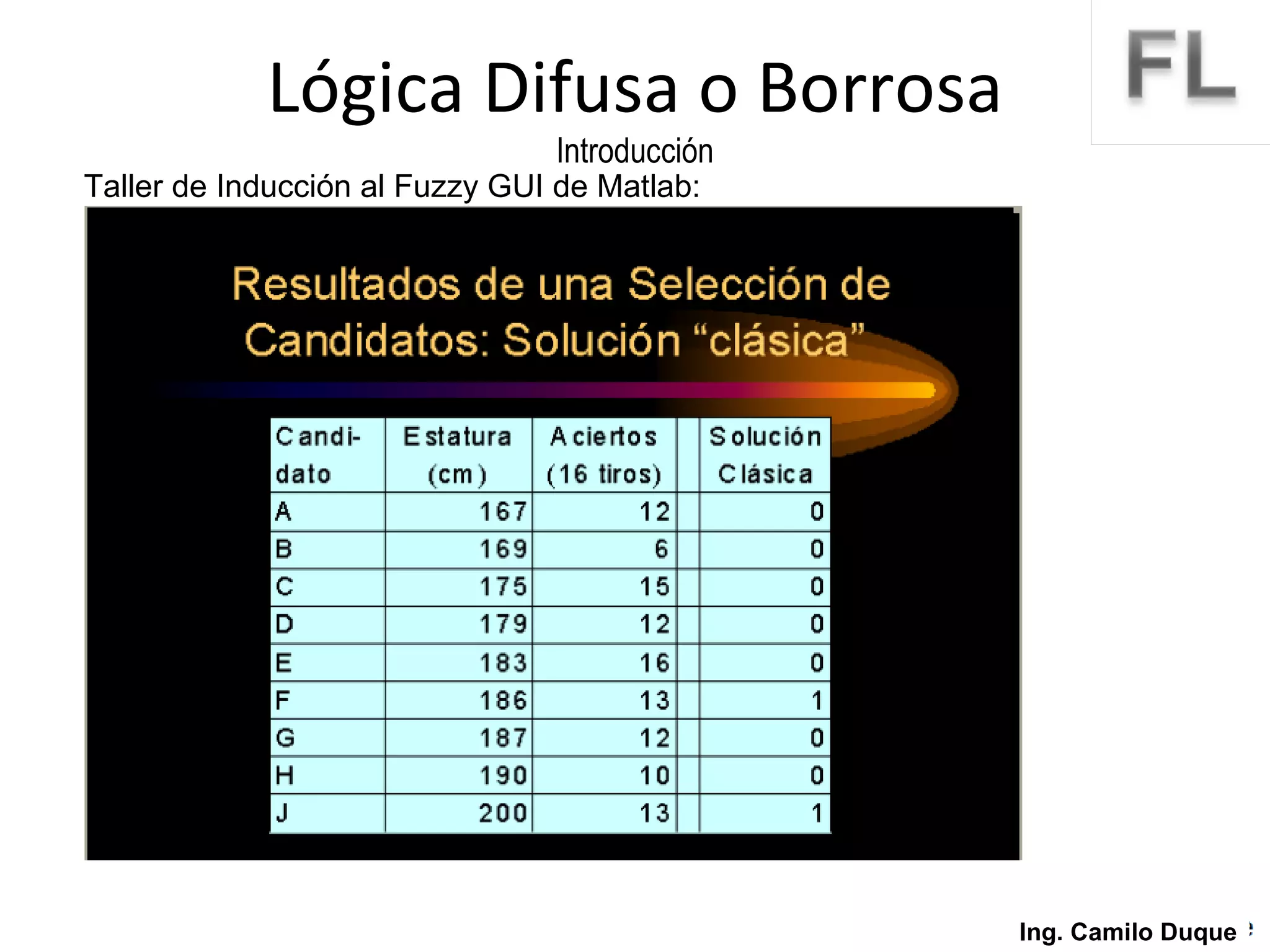
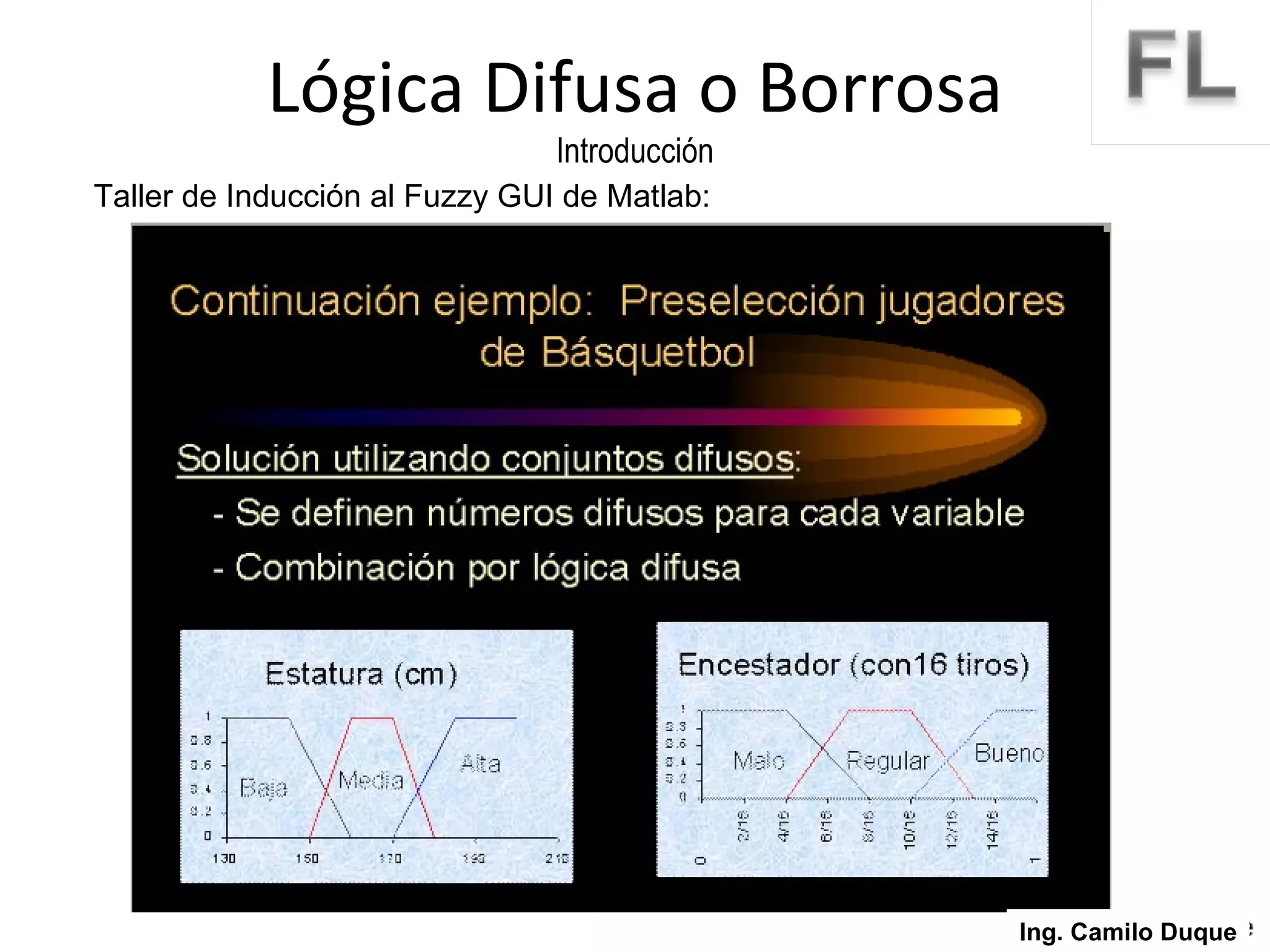
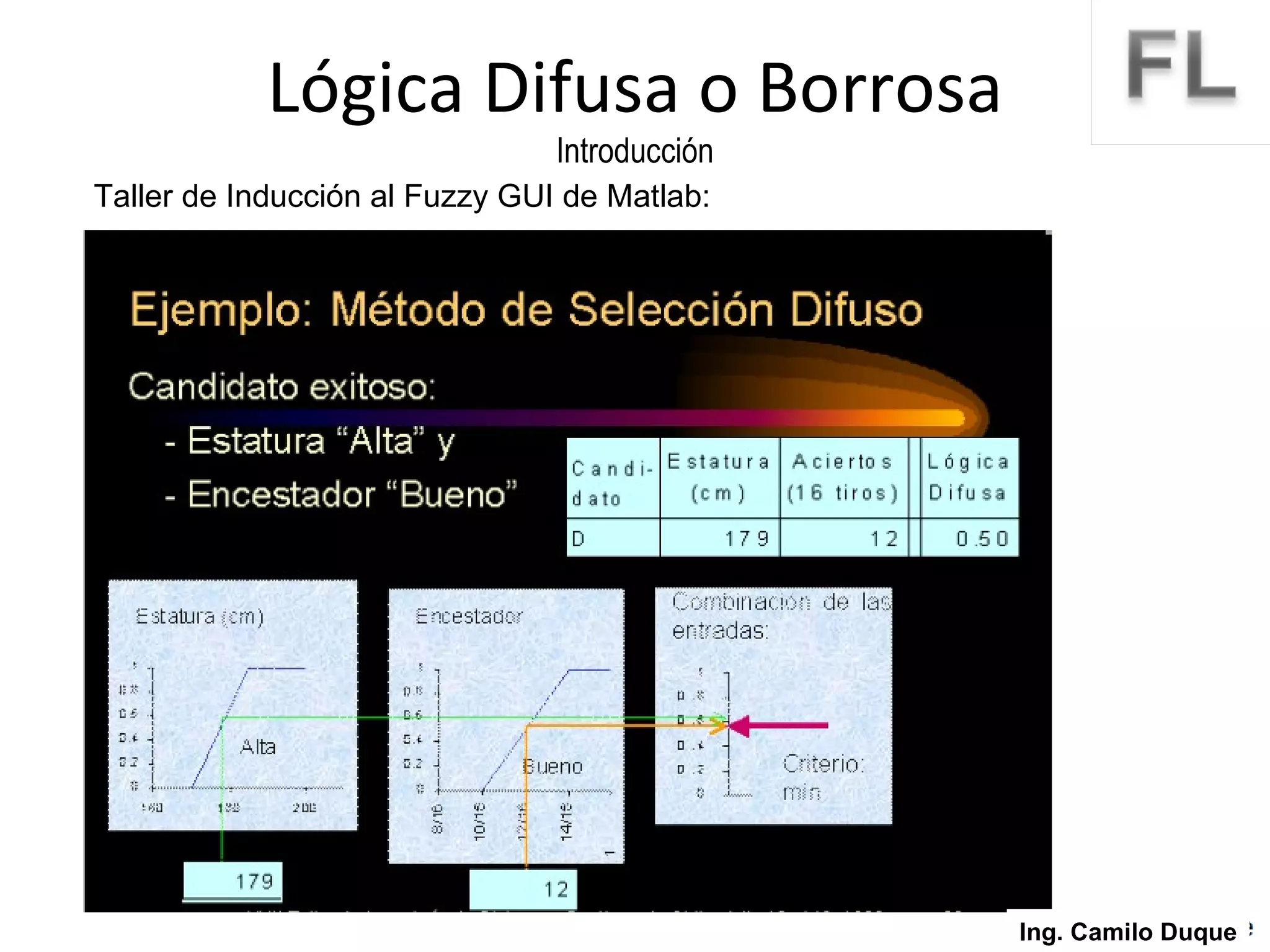
La lógica difusa surge como un intento de formalizar el conocimiento impreciso mediante conjuntos difusos y funciones de membresía. La lógica difusa fue propuesta en 1965 y desde entonces se ha aplicado en diversas áreas como control de procesos, sistemas expertos y reconocimiento de patrones. Los conjuntos difusos permiten representar conceptos vagos usando grados de pertenencia en lugar de valores booleanos.

1. Lógica Difusa o Borrosa Introducción Lógica : Ciencia que estudia las condiciones formales de validez de una inferencia y, en general, de una argumentación cualquiera. Lógica difusa surge como un intento de formalizar el conocimiento que presenta incertidumbre, vaguedad. Aborda problemas definidos en términos lingüísticos, y por tanto, imprecisos, donde la información esta expresada en términos cualitativos.

2. Lógica Difusa o Borrosa Introducción La lógica difusa fue propuesta por Zadeh 1965. 1965 Fuzzy set (Prof.. Lotfi A. Zadeh, UC Berkley) 1966 Fuzzy Logic (Dr.. Peter N. Marinos, Bell Labs.) 1972 Fuzzy Measure (Prof.. Michino Sugeno, TIT) 1974 Fuzzy Logic Controller for Steam Engine (Prof.. E.H. Mamdani, Queen Mary College, London Univ.) 1980 Control of Cement-Kiln with Monitor Capability (F.L. Smidth, Denmark) 1987 Automatic Train Operation for Sendal Subway (Hitachi) 1988 Stock Trading Expert System (Yamaichi Sequrity) 1989 Life (Laboratory for Internacional Fuzzy Engineering)

3. Lógica Difusa o Borrosa Introducción Hay que resolver varios problemas: Conseguir una representación matemática de las expresiones lingüísticas: los conjuntos difusos. Conseguir una sintaxis . Conseguir una semántica Conseguir un sistema de inferencia o razonamiento mediante el cuál inferir a partir de unos hechos borrosos unos nuevos.

4. Lógica Difusa o Borrosa Introducción Los conjuntos clásicos se pueden representar de 3 formas 1) Nombrando los elementos del conjunto Ej: A={a,e,i,o,u} 2) Definiendo una expresión que los miembros cumplan Ej: A={x| x es una letra vocal} 3) Definido por una función característica Esta función mapea los elementos del conjunto universo a los elementos del conjunto {0,1}. Para cada entonces x es miembro de A

5. Lógica Difusa o Borrosa Introducción En los conjuntos difusos la pertenencia de un elemento a un conjunto no es tan drástica como en los clásicos. El elemento puede tener un grado de membresía a dicho conjunto. En los conjuntos difusos la función característica mapea los elementos al intervalo real [0,1] Formalmente: Sea X conjunto universo clásico tal que x sean sus elementos, esto es, . Un conjunto difuso A lo definimos mediante A = { ( x, A (x) ) | x pertenece a X } Donde A(x): Función de membresía

6. Lógica Difusa o Borrosa Introducción Ejemplo: A: Conjunto de los hombres jóvenes B: Conjunto de los hombres de edad media C: Conjuntos de los hombres viejos Cada uno de los conjuntos no posee límites claros y se pueden representar mediante conjuntos difusos. Los conjuntos difusos son una forma de representar imprecisión e incertidumbre. Ing. Camilo Duque

7. Tipos de funciones de membresía En general se puede utilizar cualquier función continua que mapee los de un conjunto universo clásico dado a elementos al intervalo [0,1], las más comunes son: Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

8. Tipos de funciones de membresía En general se puede utilizar cualquier función continua que mapee los de un conjunto universo clásico dado a elementos al intervalo [0,1], las más comunes son: Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

9. Tipos de funciones de membresía En general se puede utilizar cualquier función continua que mapee los de un conjunto universo clásico dado a elementos al intervalo [0,1], las más comunes son: Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

10. Tipos de funciones de membresía En general se puede utilizar cualquier función continua que mapee los de un conjunto universo clásico dado a elementos al intervalo [0,1], las más comunes son: Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

11. Tipos de funciones de membresía En general se puede utilizar cualquier función continua que mapee los de un conjunto universo clásico dado a elementos al intervalo [0,1], las más comunes son: Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

12. Operaciones básicas sobre conjuntos difusos Las operaciones básicas en los conjuntos clásicos son 3 Unión Ej: A={a,e,i,o,u} B={b,c,d} AUB={a,e,i,o,u,b,c,d} Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

13. Intersección Ej A={1,2,3} B={2,3,4,5} ={2,3} Complemento Ej A={1,2,3} Comp(A)={4} Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

14. La extensión natural para las operaciones está dada por Unión difusa standard Intersección difusa standard Complemento difuso standard Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

15. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

16. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

17. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

18. Aplicación sencilla Supongamos que una persona cualquiera desea ir a tomar una cerveza a un local tradicional, que la cerveza sea barata y que el local quede cerca de su casa El dispone de 4 lugares conocidos Tiene sed Aquí podemos distinguir tres conjuntos difusos 1) Cerveza barata 2) Local tradicional 3) Cercanía a su hogar Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

19. Para él : Una cerveza barata es una que cueste alrededor de $1000 o menos Un local tradicional es un local que al menos tenga 5 años funcionando. Que quede cerca de su casa es que no quede a más de 10 cuadras Según las preferencias del individuo se pueden construir los siguientes conjuntos difusos: Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

20. Características de los locales Debido al planteamiento debemos intersectar los conjuntos Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

21. La solución clásica impone que Precio cerveza<=$1000 Años de servicio>=5 años Cuadras<=10 cuadras Como se deben intersectar los conjuntos, según la solución clásica el local debe estar a lo mas a 10 cuadras, tener a lo menos 5 años de servicio y que la cerveza cueste a lo más $1000 Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

22. SOLUCIÓN Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

23. Mediante la solución clásica el individuo se hubiera quedado en su hogar, lo cual no es “consistente” con la hipótesis “Tiene Sed”. Mediante la solución difusa deducimos que el individuo posiblemente hubiera ido al Local 3 a disfrutar su cerveza Lógica Difusa o Borrosa Introducción Ing. Camilo Duque

24. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque Entrada Discreta x  U n Salida Discreta y=f(x)  V DIAGRAMA DE UN SISTEMA LÓGICO BORROSO Entrada Discreta x  U n Salida Discreta y=f(x)  V REGLAS BORROSIFICA-DOR MOTOR DE INFERENCIA BORROSA DESBORROSIFI-CADOR Entrada borrosa Salida borrosa

25. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque Taller de Inducción al Fuzzy GUI de Matlab:

26. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque Taller de Inducción al Fuzzy GUI de Matlab:

27. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque Taller de Inducción al Fuzzy GUI de Matlab:

28. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque Taller de Inducción al Fuzzy GUI de Matlab:

29. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque Taller de Inducción al Fuzzy GUI de Matlab:

30. Lógica Difusa o Borrosa Introducción Ing. Camilo Duque Taller de Inducción al Fuzzy GUI de Matlab: