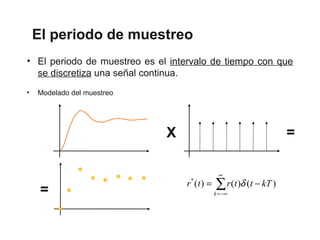
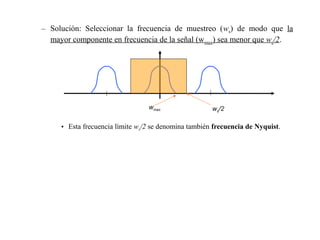
El documento describe el proceso de muestreo de señales continuas, incluyendo la frecuencia de muestreo y el aliasing. Explica que la frecuencia de muestreo debe ser al menos el doble de la frecuencia máxima de la señal para evitar el aliasing y permitir la reconstrucción de la señal original. También cubre consideraciones prácticas para la elección del periodo de muestreo en sistemas de control.

1. El periodo de muestreo
• El periodo de muestreo es el intervalo de tiempo con que
se discretiza una señal continua.
• Modelado del muestreo
X =
∞
=
r (t ) =
*
∑ r(t )δ (t − kT )
k = −∞

2. – Aplicando transformada de Fourier al tren de impulsos
∞ ∞  n
− 2π j   t
∑δ (t − kT ) = ∑ C e
k = −∞ n = −∞
n
N
• donde
∞  2πt 
1 − jn   1
∫ ∑δ (t − kT )e
T 2
Cn =  T 
dt =
T −T 2
k = −∞ T
– La señal muestreada queda
r (t ) ∞ jnwst 2π
r (t ) =
*
∑e
T n = −∞
ws =
T

3. – Aplicando transformada de Laplace
∞ r (t ) ∞ jnwst − st
R* ( s ) = ∫
−∞ T
∑ e e dt =
n = −∞
1 ∞
= ∑ R ( s ± jnws )
T n = −∞
– En el dominio frecuencial resulta
1 ∞
R* ( w) = ∑ R( j ( w ± nws ))
T n = −∞
• Esto supone una repetición del espectro de la señal original en múltiplos
enteros de la frecuencia de muestreo.
-ws ws

4. – La señal original puede recuperarse de la señal muestreada aplicando un
filtro paso bajo.
– Problema: esta recuperación no es posible cuando se producen
solapamientos en frecuencia.

5. – Esto se denomina aliasing o desdoblamiento de frecuencia.
• En el dominio temporal la interpretación es la siguiente

6. – Solución: Seleccionar la frecuencia de muestreo (ws) de modo que la
mayor componente en frecuencia de la señal (w max) sea menor que ws/2.
wmax ws/2
• Esta frecuencia límite ws/2 se denomina también frecuencia de Nyquist.

7. Elección del periodo de muestreo
• Consideraciones teóricas:
– El periodo de muestreo
debe ser inferior a la mitad
del menor periodo de
oscilación del sistema a
controlar.

8. • Consideraciones prácticas:
– Compromiso coste/prestaciones:
• Interesa un periodo de muestreo grande para reducir el coste de diversos
elementos del sistema de control: microprocesador, sensores,
muestreadores, etc.
• Interesa un periodo de muestreo pequeño para mejorar la estabilidad,
precisión en régimen permanente, rechazo de perturbaciones, etc.
– En función de los parámetros del sistema:
• Frecuencia de muestreo de 6 a 10 veces el ancho de banda.
• Periodo de muestreo de 1/2 a 1/4 del tiempo de subida.
• Período de muestreo de 1/10 o 1/20 veces el Tss

9. – Algunos ejemplos prácticos:
• De 1 a 3 segundos para control de flujo.
• De 5 a 10 segundos para control de nivel.
• De 1 a 5 segundos para control de presión.
• De 10 a 20 segundos para control de temperatura.

10. • Es deseable que el periodo de muestreo sea lo más
estable posible.
– Mejor ajuste entre los resultados de las simulaciones y el sistema real.
– Hay que evitar incluir en medio del bucle de control instrucciones con
tiempo de ejecución variable.
– Para valores pequeños sólo puede garantizarse en sistemas operativos de
tiempo real o con hardware dedicado.

11. Ejemplos de respuesta

18. Comportamiento entre los
intervalos de muestreo
• El diseño discreto sólo garantiza el
comportamiento del sistema en los instantes de
muestreo.
– Se precisan métodos para
obtener la respuesta del
sistema con una
resolución mayor.

19. Efectos de la cuantificación
• Fuentes de imprecisión:
– Errores en la codificación de los valores de los coeficientes
del controlador y otras constantes del sistema.
– Errores de cuantificación en la digitalización de las señales.
– Errores de desbordamiento en las operaciones del algoritmo
de control.