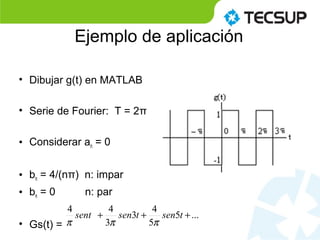
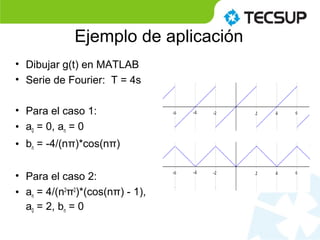
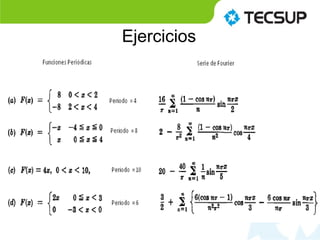
El documento presenta el uso de MATLAB para resolver series de Fourier, enfocándose en su interpretación y aplicación en funciones periódicas. Se explica que una serie de Fourier descompone una función periódica en una suma infinita de funciones senoidales. También se mencionan ejemplos de aplicación y ejercicios prácticos relacionados con series de Fourier.

1. Matemática Aplicada
Profesor: Mg. Ing. Daniel Mendoza
jmendozar@tecsup.edu.pe

2. Matemática Aplicada
Aplicaciones de MATLAB a la solución
de Series de Fourier

3. 3
Series de Fourier
"Series de Fourier, Transformadas de Fourier y Aplicaciones",
Genaro González

4. Aplicaciones de MATLAB a la solución
de Series de Fourier
• Objetivos:
• Interpretar el concepto de la serie de Fourier.
• Utilizar MATLAB para aproximar diversas
funciones periódicas mediante series de Fourier.

5. Introducción
• ¿Qué es una serie?
• Una serie es una suma infinita, en este caso, de
funciones. Dos ejemplos de series importantes
son las siguientes:
• S. de Taylor: Base  Polinomio
• S. de Fourier: Base  Funciones seno / coseno

6. Serie de Fourier
• Una serie de Fourier es una serie infinita que
converge puntualmente a una función periódica
y continua a trozos (o por partes). Las series de
Fourier constituyen la herramienta matemática
básica del análisis de Fourier empleado para
analizar funciones periódicas a través de la
descomposición de dicha función en una suma
infinita de funciones senoidales mucho más
simples (como combinación de senos y cosenos
con frecuencias enteras).

7. Serie de Fourier
• El nombre se debe al matemático francés Jean-
Baptiste Joseph Fourier que desarrolló la teoría
cuando estudiaba la ecuación del calor. Fue el
primero que estudió tales series
sistemáticamente, y publicando sus resultados
iniciales en 1807 y 1811. Esta área de
investigación se llama algunas veces Análisis
armónico.

8. Ejemplo de aplicación
• Dibujar g(t) en MATLAB
• Serie de Fourier: T = 2π
• Considerar an = 0
• bn = 4/(nπ) n: impar
• bn = 0 n: par
• Gs(t) =
...5
5
4
3
3
44
+++ tsentsensent
πππ

9. Ejemplo de aplicación
• Dibujar g(t) en MATLAB
• Serie de Fourier: T = 4s
• Para el caso 1:
• a0 = 0, an = 0
• bn = -4/(nπ)*cos(nπ)
• Para el caso 2:
• an = 4/(n2
π2
)*(cos(nπ) - 1),
a0 = 2, bn = 0

10. Ejercicios