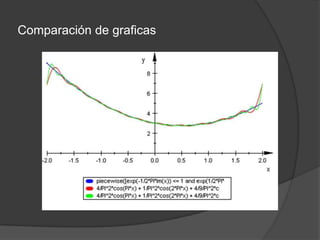
El documento explica los conceptos básicos de las series de Fourier, incluyendo su uso para representar funciones periódicas mediante la suma de senos y cosenos. Describe algunas aplicaciones importantes de las series de Fourier en el análisis de señales y en áreas como acústica y procesamiento de imágenes.































![Grafica de la función cuando tiende a un
numero entero en este caso [1..10]](https://image.slidesharecdn.com/seriedefourierok-130722220735-phpapp01/85/Series-de-fourier-32-320.jpg)
![Grafica de la función cuando tiende a un
numero entero en este caso [1..20]](https://image.slidesharecdn.com/seriedefourierok-130722220735-phpapp01/85/Series-de-fourier-33-320.jpg)
![Grafica de la función cuando tiende al infinito [1..∞]](https://image.slidesharecdn.com/seriedefourierok-130722220735-phpapp01/85/Series-de-fourier-34-320.jpg)