Este documento describe un experimento para estudiar el comportamiento de un péndulo simple. Los estudiantes midieron el período de oscilación para varias longitudes de cuerda y utilizaron estos datos para calcular el valor de la gravedad. El resumen experimental incluye tablas de datos de períodos de tiempo, cálculos de la gravedad y un análisis de errores.

1. PENDULO SIMPLE
Cesar Barahona 701601
Daniel Quevedo 503189
Nelson Villero 504244
Andrés Nieto 537664
Daniel Ospina 502358
RESUMEN : el desarrollo de este laboratorio se
centra en comprender el comportamiento físico de
un péndulo simple, para ello se debe entender de
manera clara los conceptos tales como periodo,
frecuencia, gravedad, entre otros que influyen o
hacen parte del sistema a analizar bien sea
mediante el análisis conceptual (físico) y por qué
no a partir de cada uno de los datos registrados,
teniendo la capacidad de interpretarlos
describiendo teóricamente lo que cada uno de
estos muestra generados por el comportamiento
general del sistema, en este caso el péndulo
simple. El manejo de la linealizacion de datos
experimentales (medidas directas e indirectas), es
de vital importancia ya que a partir de estos se
puede entender el procedimiento que tiene como
fin predecir el comportamiento del sistema.
I. INTRODUCCION
En el presente laboratorio se evidencia la
capacidad que se tiene de interpretar y relacionar
datos y resultados experimentales, con modelos
teóricos, mediante la realización de prácticas
experimentales para poder determinar la validez y
exactitud de los mismos, con el fin de entender el
comportamiento físico de un péndulo simple y así
identificar sus características tales como su
movimiento periódico, el cual consiste en una
masa suspendida de una cuerda, de masa
despreciable que oscila dentro de un intervalo de
tiempo, determinando tal comportamiento por
método grafico y transitoriamente verificarlo con
los valores teóricos calculados; teniendo en cuenta
características tales como la gravedad, periodo,
longitud (cuerda) y masa; que se encuentran
implícitos en el análisis que se hará en este
sistema (péndulo simple).
Posteriormente categorizar y tabular cada uno de
los datos con sus correspondientes unidades e
incertidumbres y así poder determinar el
comportamiento físico del péndulo que es
básicamente lo que esta explicito paso por paso
en el contenido de este laboratorio y cada una de
las partes, procedimientos, muestras (datos y
gráficos) que lo conforman.
II. OBEJTIVO
Calcular el valor teórico y experimental de la
gravedad generada en este practica.
III. MARCO TEORICO
Aspecto Teórico: Un péndulo simple se define
como una partícula de masa m suspendida del
punto O por un hilo inextensible de longitud l y de
masa despreciable, como muestra la [Figura 1]; si

2. la partícula se desplaza a una posición x (ángulo
que hace el hilo con la vertical) y luego se suelta,
el péndulo comienza a oscilar. Naturalmente es
imposible la realización práctica de un péndulo
simple, pero si es accesible a la teoría. El péndulo
simple se denomina así en contraposición a los
péndulos reales, compuestos o físicos, únicos que
pueden construirse.
[Figura 1]
El péndulo describe una trayectoria circular, un
arco de una circunferencia de radio l. las fuerzas
que actúan sobre la partícula (masa m) son dos el
peso mg (gravedad g) y la tensión (T) del hilo o
cuerda, el ángulo está representado (θ). Como
pauta importante a tener en cuenta a la hora de
analizar el comportamiento del péndulo simple es
que este es un caso de movimiento periódico el
cual presenta un periodo y una frecuencia angular
dados por la expresión que se muestra a
continuación:
Donde W representa a la frecuencia angular y T al
periodo cada uno correspondiente al sistema
péndulo simple, entre tanto la longitud de la
cuerda está representada por L y la gravedad
respectivamente con g. Como se puede observar
en la segunda expresión el periodo T no depende
de la geometría ni de la masa del cuerpo que
oscila o se mueve.
Conceptos
El período de una oscilación (T) es el número de
variaciones necesarias para que dicha oscilación
vuelva a ser representada por cualquiera de los
valores anteriores obtenidos, con un índice de
cadencia regular.
La gravedad (g), es la fuerza de atracción a que
está sometido todo cuerpo que se halle en las
proximidades de la Tierra.
La frecuencia o velocidad angular es una
medida de la velocidad de rotación. Se define
como el ángulo girado por una unidad de tiempo y
se designa mediante (W). Su unidad en el Sistema
Internacional es el radián por segundo (rad/s).
La Frecuencia es una magnitud que mide el
número de repeticiones por unidad de tiempo de
cualquier fenómeno o suceso periódico.

3. IV. MONTAJE EXPERIMENTAL
[Figura 2]
Montaje Experimental (imagen tomada de
http://carolina2010.wordpress.com/laboratorio-de-
pendulo-simple/)
Como muestra la [Figura 2] el montaje
experimental está compuesto por un soporte o
pinza, hilo, masa, soporte, base del soporte, regla
que permite medir las distintas longitudes de
cuerdas que se tomaron para cada tiempo u
oscilación diferentes y precisamente se hizo uso
de un cronometro para medir el tiempo. NOTA: los
ángulos para todas las longitudes fueron
equivalentes a 10 grados estos se midieron con un
transportador que fue fijado en la parte superior
del soporte.
Luego de conocer el montaje experimental se
procede a contabilizar el tiempo para cada una de
las longitudes a medirse, en cuanto a la masa va
ser siempre la misma para toda la práctica
experimental y así se van registrando cada uno de
los datos con sus correspondientes incertidumbres
y unidades.
V. RESULTADOS
Procedimiento: en la tabla No. 1 se registran
cada una de las distintas longitudes de la cuerda y
sus tiempos correspondientes.
I (cm) t1(s) ± t2(s) ± t3(s) ±
43 9,12±0,01 9,06±0,01 9,04±0,01
48 9,63±0,01 9,56±0,01 9,66±0,01
53 10,31±0,01 10,63±0,01 10,09±0,01
58 10,5±0,01 10,59±0,01 10,56±0,01
63 10,94±0,01 10,94±0,01 11±0,01
68 11,5±0,01 11,57±0,01 11,28±0,01
73 11,63±0,01 11,84±0,01 12,02±0,01
Tabla No.1
En la tabla No. 1 se encuentran registrados las
distintas longitudes (verde), entre tanto cada
tiempo evidentemente se tomo en segundos (s) y
su incertidumbre corresponde al cronometro.
En la tabla No. 2 aparece registrado el tiempo
promedio y el valor de los periodos para cada
tiempo y longitud
I (cm) t promedio(s) ± T(S)
43 9,07±0,29 1,30±0,01
48 9,62±0,29 1,37±0,01
53 10,18±0,29 1,45±0,01
58 10,55±0,29 1,51±0,01
63 10,96±0,29 1,57±0,01
68 11,45±00,29 1,64±0,01
73 11,83±0,29 1,69±0,01
Tabla No. 2
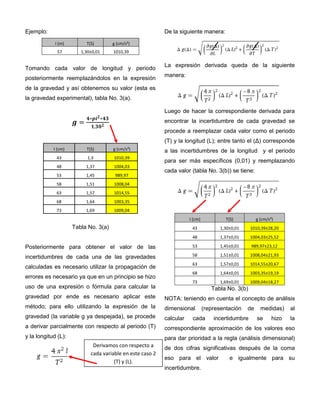
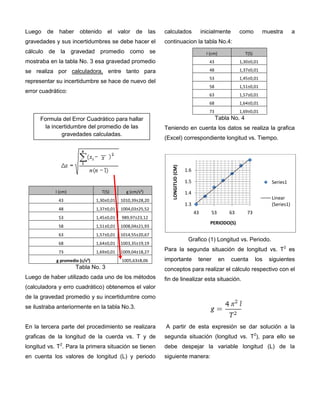
De los datos de la tabla No. 2 se observa el tiempo
promedio (s) que fue calculado mediante la
calculadora y su respectiva incertidumbre se
calculo por el método de error cuadrático.
Formula del Error Cuadrático para hallar
la incertidumbre del promedio de los
tiempos calculados.

4. Entre tanto la incertidumbre del Periodo (T),
corresponde a la misma del tiempo es decir la del
cronometro esto ya que para hallar cada una de
los periodos se utilizo la expresión:
T= (t TOTAL)/ (Nº Oscilaciones)
Donde T corresponde al periodo que va ser
equivalente a t TOTAL que equivale al tiempo total
registrado para cada una de las longitudes, sobre
el número de oscilaciones que en este caso para
todos fue de 7 en total.
En la segunda parte del procedimiento se procede
hallar la gravedad con cada pareja de datos de
longitud y periodo calculados anteriormente y que
se evidenciaron en la tabla No. 2 cada uno con su
correspondiente incertidumbre. En la tabla No. 3
que se muestra a continuación se registra el valor
de la gravedad y su correspondiente
incertidumbre. Para ello se reescribirá en esta
tabla los mismos valores referentes a la longitud
(de la cuerda) y el periodo de las mismas cada
uno también con sus correspondientes
incertidumbres y unidades.
I (cm) T(S) g (cm/s²)
43 1,30±0,01 1010,39±28,20
48 1,37±0,01 1004,03±25,52
53 1,45±0,01 989,97±23,12
58 1,51±0,01 1008,04±21,93
63 1,57±0,01 1014,55±20,67
68 1,64±0,01 1003,35±19,19
73 1,69±0,01 1009,04±18,27
g promedio (cm/s²) 1005,63±8,06
Tabla No. 3
En la tabla se muestra los valores de cada
gravedad calculados para el cálculo de cada valor
se hizo uso de una ecuación o expresión
correspondiente que se muestra a continuación:
La expresión anterior corresponde al cálculo del
periodo (T) que depende de una longitud (L) y el
valor de la gravedad (g), “usada en el péndulo
simple”, pero para el calcular el valor de la
gravedad que se muestra en la tabla No. 3 es
necesario despejar la gravedad (g) de la anterior
expresión luego de ello se obtiene que:
Luego de obtener el despeje correspondiente de la
gravedad (g) se hace el reemplazo en la ecuación
de cada uno de los valores longitud (L) y periodo
(T) que aparecen en la tabla No. 3.

5. Ejemplo:
I (m) T(S) g (cm/s²)
57 1,30±0,01 1010,39
Tomando cada valor de longitud y periodo
posteriormente reemplazándolos en la expresión
de la gravedad y así obtenemos su valor (esta es
la gravedad experimental), tabla No. 3(a).
I (cm) T(S) g (cm/s²)
43 1,3 1010,39
48 1,37 1004,03
53 1,45 989,97
58 1,51 1008,04
63 1,57 1014,55
68 1,64 1003,35
73 1,69 1009,04
Tabla No. 3(a)
Posteriormente para obtener el valor de las
incertidumbres de cada una de las gravedades
calculadas es necesario utilizar la propagación de
errores es necesario ya que en un principio se hizo
uso de una expresión o fórmula para calcular la
gravedad por ende es necesario aplicar este
método; para ello utilizando la expresión de la
gravedad (la variable g ya despejada), se procede
a derivar parcialmente con respecto al periodo (T)
y la longitud (L):
De la siguiente manera:
La expresión derivada queda de la siguiente
manera:
Luego de hacer la correspondiente derivada para
encontrar la incertidumbre de cada gravedad se
procede a reemplazar cada valor como el periodo
(T) y la longitud (L); entre tanto el (Δ) corresponde
a las incertidumbres de la longitud y el periodo
para ser más específicos (0,01) y reemplazando
cada valor (tabla No. 3(b)) se tiene:
I (cm) T(S) g (cm/s²)
43 1,30±0,01 1010,39±28,20
48 1,37±0,01 1004,03±25,52
53 1,45±0,01 989,97±23,12
58 1,51±0,01 1008,04±21,93
63 1,57±0,01 1014,55±20,67
68 1,64±0,01 1003,35±19,19
73 1,69±0,01 1009,04±18,27
Tabla No. 3(b)
NOTA: teniendo en cuenta el concepto de análisis
dimensional (representación de medidas) al
calcular cada incertidumbre se hizo la
correspondiente aproximación de los valores eso
para dar prioridad a la regla (análisis dimensional)
de dos cifras significativas después de la coma
eso para el valor e igualmente para su
incertidumbre.
Derivamos con respecto a
cada variable en este caso 2
(T) y (L).

6. Luego de haber obtenido el valor de las
gravedades y sus incertidumbres se debe hacer el
cálculo de la gravedad promedio como se
mostraba en la tabla No. 3 esa gravedad promedio
se realiza por calculadora, entre tanto para
representar su incertidumbre se hace de nuevo del
error cuadrático:
I (cm) T(S) g (cm/s²)
43 1,30±0,01 1010,39±28,20
48 1,37±0,01 1004,03±25,52
53 1,45±0,01 989,97±23,12
58 1,51±0,01 1008,04±21,93
63 1,57±0,01 1014,55±20,67
68 1,64±0,01 1003,35±19,19
73 1,69±0,01 1009,04±18,27
g promedio (c/s²) 1005,63±8,06
Tabla No. 3
Luego de haber utilizado cada uno de los métodos
(calculadora y erro cuadrático) obtenemos el valor
de la gravedad promedio y su incertidumbre como
se ilustraba anteriormente en la tabla No.3.
En la tercera parte del procedimiento se realizara
graficas de la longitud de la cuerda vs. T y de
longitud vs. T2
. Para la primera situación se tienen
en cuenta los valores de longitud (L) y periodo
calculados inicialmente como muestra a
continuacion la tabla No.4:
I (cm) T(S)
43 1,30±0,01
48 1,37±0,01
53 1,45±0,01
58 1,51±0,01
63 1,57±0,01
68 1,64±0,01
73 1,69±0,01
Tabla No. 4
Teniendo en cuenta los datos se realiza la grafica
(Excel) correspondiente longitud vs. Tiempo.
Grafico (1) Longitud vs. Periodo.
Para la segunda situación de longitud vs. T2
es
importante tener en cuenta los siguientes
conceptos para realizar el cálculo respectivo con el
fin de linealizar esta situación.
A partir de esta expresión se dar solución a la
segunda situación (longitud vs. T2
), para ello se
debe despejar la variable longitud (L) de la
siguiente manera:
1.3
1.4
1.5
1.6
43 53 63 73
LONGITUD(CM)
PERIODO(S)
Series1
Linear
(Series1)
Formula del Error Cuadrático para hallar
la incertidumbre del promedio de las
gravedades calculadas.

7. Para poder representar gráficamente esta
expresión que fue despejada con respecto a la
longitud (L) debemos aplicar logaritmos con el fin
de predecir la ecuación del grafico.
Luego de haber aplicado logaritmos es importante
tener en cuenta que:
Y= ln L.
B= ln (g/4π2
).
M= 2.
X= ln T.
Para el cálculo de cada parte de la expresión
obtenida es necesario tener presente que:
10b
= g/4π2
.
B= log10 (g/4π2
).
M= 2.
Se calcula la gravedad g= 10b
(4π2
).
Reemplazando cada uno de los valores en cada
expresión se obtiene los datos correspondientes
para generar el grafico de la longitud vs. T2
. Estos
datos se muestran en la tabla No. 5:
b 10^b I (cm) g (cm/s²)
1,41 25,59 43 1010,39
1,41 25,43 48 1004,03
1,40 25,08 53 989,97
1,41 25,53 58 1008,04
1,41 25,70 63 1014,55
1,41 25,42 68 1003,35
1,41 25,56 73 1009,04
Tabla No. 5
Los valores finales que se calcularon se muestran
en la tabla No. 5 y estos satisfacen la ecuación de
la grafica que se muestra a continuacion:
Grafico (2) Longitud vs. T2
.
En la cuarta parte del procedimiento se
determinara el valor de la gravedad por método
grafico mediante el ajuste lineal por mínimos
cuadrados dado por la siguiente expresión y
donde se reemplazaran los datos
correspondientes, se debe tener en cuenta que
por el ajuste lineal de mínimos cuadrados
obtenemos el valor de m y b, donde m representa
el valor de la pendiente y aplicamos la siguiente
fórmula:
Luego de aplicar la formula anterior obtenemos
que la ecuación de la recta es:
Y=25,494x - 0,1273.
2.86, 73
43
53
63
73
1.69 2.19 2.69
LONGITUD(CM)
T^2(S^2)
LONGITUD VS T^2

8. Luego de obtener la ecuación de la recta
deducimos el valor de la gravedad y su
incertidumbre por método grafico estos valores se
muestran en la tabla No. 6 (Tabla Comparativa),
pero antes se muestra la grafica de la ecuación de
la recta calculada:
Grafico (3) Ajuste Lineal
Valor Experimental de la Gravedad.
V. Teórico V. Experimental V. Experimental Grafico
9,800 Cm/s
2
1005,63±8,06 25,94±0,24
Tabla No. 6 Tabla Comparativa.
VI. Aspecto teórico (análisis de resultados).
Compare el valor teórico de la gravedad (el
reportado por Bogotá) con los valores
experimentales. ¿Qué tan exacto es cada uno de
los valores obtenidos con respecto a la gravedad
teórica? ¿Cuál de los dos métodos son más
precisos?
El valor reportado por Bogotá en cuanto a la
gravedad es de 9,773883709 m/s2
, el valor que
presenta más aproximación con respecto al valor
teórico formulado es el valor experimental
calculado ya que su diferencia al teórico es
mínimo y su similitud es casi igual.
En el desarrollo del procedimiento nos
pudimos dar cuenta que cada uno de los datos
calculados representan o deben tener cierto
grado de exactitud bien sean calculados
mediante instrumentos o a partir de
expresiones o ecuaciones (medidas directas e
indirectas) y que implica tener cierta claridad
en el manejo de los conceptos para poder
interpretarlos.
En cuanto a los valores teóricos calculados al final
nos damos cuenta que las diferencias de unos con
otros NO son tan diferentes esto indica que cada
uno de los datos calculados representan cierto
grado de exactitud desde el inicio de la práctica,
durante y después de la misma.
CONCLUSIONES
El presente laboratorio nos ha permitido identificar
el método correcto y adecuado que se debe
utilizar para el registro de los datos experimentales
teniendo en cuenta los criterios provenientes de
allí. (Aspecto teórico).
El análisis y procesamiento de cada uno de los
datos tomados con respecto al montaje
experimental, los tiempos, y cada una de las
longitudes que se marcaron en el procedimiento
(en cuanto al péndulo) y que nos permitieron
identificar de manera clara el concepto de péndulo
y = 25,494x - 0,1273
43
48
53
58
63
68
73
1.69 2.19 2.69

9. simple y todas sus características que hacen parte
de la temática del presenta laboratorio.
A partir de los datos experimentales que se
obtuvieron en el laboratorio se ha podido
establecer las diferencias entre los conceptos que
intervienen en el momento de analizar el
comportamiento físico de un péndulo o cualquier
otro sistema derivado de este; y a su vez
interpretarlos de manera clara y así evaluar tal
comportamiento de la mejor forma.
BIBLIOGRAFIA
[1] Mecánica Experimental para Ciencias e
Ingeniería, Mario Enrique Álvarez Ramos.
[2] Introducción al análisis de datos
experimentales, Roque Serrano Gallego.
[3]
http://www.sc.ehu.es/sbweb/fisica/dinamica/trabajo
/pendulo/pendulo.htm.
[4] Física para la ciencia y la tecnología:
Oscilaciones y Ondas. Paull Allen Tipler, Gene
Mosca, 2005.
[5] http://carolina2010.wordpress.com/laboratorio-
de-pendulo-simple/.