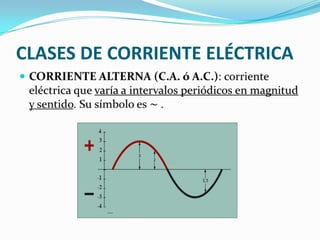
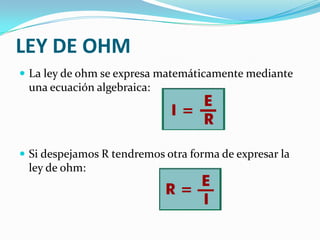
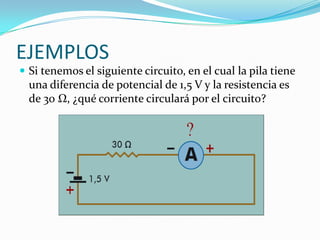
Este documento describe las leyes fundamentales de la corriente eléctrica. Explica que la corriente eléctrica es el flujo de electrones impulsado por una diferencia de potencial, y que requiere de un circuito completo. Además, define las magnitudes eléctricas básicas como la intensidad, tensión y resistencia, y establece las relaciones matemáticas entre ellas descritas por las leyes de Ohm y Watt.

1. La corriente eléctrica es transmisión de energía,
por lo cual se desplaza aproximadamente a
300,000 Km por segundo, y debe existir
necesariamente un circuito que permita este flujo
constante de electrones, entre la fuente y una
carga, donde la energía eléctrica se transforma en
otras formas de energía: luz, calor, movimiento
mecánico, etc.

2. CORRIENTE ELÉCTRICA

3. CLASES DE CORRIENTE ELÉCTRICA
 CORRIENTE CONTINUA (C.C. ó DC): corriente
eléctrica que no varía ni en magnitud ni en sentido. Su
símbolo es ---------, _________

4. CLASES DE CORRIENTE ELÉCTRICA


5. MAGNITUDES ELÉCTRICAS
FUNDAMENTALES
INTENSIDAD, amperaje o simplemente corriente (I): es
la cantidad de electrones que circula por un conductor
en unidad de tiempo. La unidad que se emplea para
medir esta magnitud es el amperio.
Múltiplos:
Kiloamperio (kA): equivale a 1.000 A.
kA = 1.000A = 10³ A

6. MAGNITUDES ELÉCTRICAS
FUNDAMENTALES
Submúltiplos:
miliamperio (mA): equivale a la milésima parte de un
amperio.
mA = 0,001 A = 10¯³ A
microamperio (μA): equivale a la millonésima parte de
un amperio.
μA = 0,000001 A = 10¯⁶ A

7. MAGNITUDES ELÉCTRICAS
FUNDAMENTALES
TENSIÓN, Es la diferencia de los potenciales que existe
en los extremos de una carga eléctrica o entre dos
conductores ( E ó U ). La unidad que se emplea para
medir esta magnitud es el voltio.
Múltiplos:
Kilovoltio (kV): equivale a 1.000 V
kV = 1.000 V = 10³ V
Megavoltio (MV): equivale a 1’000.000 V
MV = 1’000.000 V = 10⁶ V

8. MAGNITUDES ELÉCTRICAS
FUNDAMENTALES
Submúltiplos:
milivoltio (mV): equivalente a la milésima parte de un
voltio
mV = 0,001 V = 10¯³ V
microvoltio (μV): es equivalente a la millonésima parte
de un voltio
μV = 0,000001 V = 10¯⁶ V

9. MAGNITUDES ELÉCTRICAS
FUNDAMENTALES
RESISTENCIA (R), es la oposición o dificultad que
ofrece un conductor al paso de la corriente. La unidad
que se emplea para medir esta magnitud es el ohmio.
Múltiplos:
kilohmio (kΩ): es equivalente a 1.000Ω= 10³ Ω
Megohmio (MΩ): equivalente a 1’000.000 Ω = 10⁶ Ω

10. LEY DE OHM
 Para poder tener corriente eléctrica es necesario que
exista una diferencia de potencial entre dos cargas, la
cual hará que empiecen a circular los electrones a
través de los conductores, quienes a su vez presentarán
mayor o menor resistencia al movimiento o flujo de
dichos electrones. Es decir que las tres magnitudes
fundamentales están íntimamente relacionadas entre
sí, aspecto que fue comprobado mediante una serie de
experimentos por Georg Simon Ohm.

11. LEY DE OHM
 Ohm descubrió que si en un circuito de DC se
mantenía constante la resistencia y se aumentaba la
tensión, se producía también un aumento equivalente
en la corriente. De la misma manera una disminución
en la tensión genera una disminución equivalente en la
corriente.

12. LEY DE OHM
 La conclusión que sacó Ohm fue que:
LA CORRIENTE ES DIRECTAMENTE
PROPORCIONAL A LA TENSIÓN.
Además observó que si se mantenía constante la tensión
de la fuente y se aumentaba el valor de la resistencia, la
intensidad disminuía. Por el contrario si disminuía el
valor de la resistencia, la intensidad aumentaba. Así
obtuvo una segunda conclusión:
LA CORRIENTE ES INVERSAMENTE
PROPORCIONAL A LA RESISTENCIA.

13. LEY DE OHM
 Estas dos conclusiones dieron origen a la LEY DE OHM
que dice:
LA INTENSIDAD ES
DIRECTAMENTE PROPORCIONAL
A LA TENSIÓN E INVERSAMENTE
PROPORCIONAL A LA
RESISTENCIA.

14. LEY DE OHM
 La ley de ohm se expresa matemáticamente mediante
una ecuación algebraica:
 Si despejamos R tendremos otra forma de expresar la
ley de ohm:

15. LEY DE OHM
 Si despejamos E tendremos la siguiente expresión:
 Gracias a estas tres expresiones matemáticas, siempre
que conozcamos dos de las tres magnitudes podemos
averiguar la que se desconoce. En los cálculos se usan
únicamente las unidades básicas.

16. EJEMPLOS
 Si tenemos el siguiente circuito, en el cual la pila tiene
una diferencia de potencial de 1,5 V y la resistencia es
de 30 Ω, ¿qué corriente circulará por el circuito?

17. EJEMPLOS
I = E/R
I = 1,5V / 30Ω
I = 0,05 A = 50mA
Averiguar el valor de la resistencia del siguiente circuito:

18. EJEMPLOS
R = E/I
R = 1,5 V/150 mA
Debemos convertir todas las unidades a unidabásicas: 150 mA = 0,15 A
R = 1,5 V/0,15 A
R = 10 Ω
des

19. EJEMPLOS
Averiguar la tensión que debe tener la fuente
alimenta el siguiente circuito:
que

20. EJEMPLOS
E=IxR
E = 75 mA x 1600 Ω
Debemos convertir todas las magnitudes a unidades
básicas: 75 mA = 0,075 A
E = 0,075 A x 1600 Ω
E = 120 V

21. LEY DE WATT
Si se aplica una diferencia de potencial a un circuito, éste
será recorrido por una determinada cantidad de
corriente eléctrica que se transformará en otra forma de
energía (luz, calor, movimiento mecánico, etc.),
realizándose de esta manera un trabajo eléctrico, el cual
será proporcional a la tensión y a la cantidad de corriente
que recorra el circuito.

22. LEY DE WATT
 Como un mismo trabajo puede realizarse en tiempos
diferentes, la rapidez con que éste se realice se llamará
potencia y se expresará en unidades de trabajo (cuya
unidad es el julio y que se define como el trabajo
efectuado por un columbio, con una diferencia de
potencial de un voltio) y de tiempo (cuya unidad es el
segundo).

23. LEY DE WATT
Con base en estas dos unidades, la POTENCIA
ELÉCTRICA (P) se define como el trabajo eléctrico que
se realiza en una unidad de tiempo, y cuya unidad básica
de medida es el vatio.
VATIO ó WATT (W): es el trabajo realizado cuando fluye
un amperio, con una diferencia de potencial de un voltio.

24. LEY DE WATT
Múltiplos:
Kilovatio (kW) = 1.000 W = 10³ W
Megavatio (MW) = 1’000.000W = 10⁶ W
Gigavatio (GW) = 1.000’000.000W = 10⁹ W
El instrumento que se usa para medir potencia eléctrica
en el vatímetro.

25. LEY DE WATT
La ley de watt nos expresa la relación existente entre la
potencia, la intensidad y la tensión y se enuncia de la
siguiente manera:
LA POTENCIA ES DIRECTAMENTE
PROPORCIONAL A LA INTENSIDAD Y A LA
TENSIÓN

26. LEY DE WATT
La ley de watt se expresa matemáticamente con la
siguiente ecuación:
Si despejamos E tendremos otra forma de expresar la ley
de watt:

27. LEY DE WATT
Si despejamos I en lugar de E, tendremos la siguiente
expresión:

28. RELACIONES QUE SE PUEDEN ESTABLECER
ENTRE LAS LEYES DE OHM Y WATT
En este circuito es posible averiguar la potencia de la
resistencia

29. RELACIONES QUE SE PUEDEN ESTABLECER
ENTRE LAS LEYES DE OHM Y WATT
Si observamos bien la ley de ohm y la ley de watt, nos
daremos cuenta que en realidad en ambas leyes se
emplean exactamente las mismas mag-nitudes.
Por la ley de ohm sabemos que la intensidad, ten sión y
resistencia están íntimamente relacionadas entre sí, por
consiguiente en la ley de watt, de alguna forma deberá
estar también la resistencia,

30. RELACIONES QUE SE PUEDEN ESTABLECER
ENTRE LAS LEYES DE OHM Y WATT
siendo posible averiguar la potencia en función de la
resistencia. Veámoslo matemáticamente:
P = I E ley de watt
E = I R ley de ohm
sustituyendo el valor de E en la primera ecuación
P=IxIR
P = I²R

31. RELACIONES QUE SE PUEDEN ESTABLECER
ENTRE LAS LEYES DE OHM Y WATT
De igual manera:
P = I E ley de watt
I = E / R ley de ohm
 sustituyendo el valor de I en la primera ecuación
 P = ExE/R
 P = E² / R

32. RELACIONES QUE SE PUEDEN ESTABLECER
ENTRE LAS LEYES DE OHM Y WATT
Con estas aclaraciones podemos afirmar que sí es posible
averiguar la potencia de la resistencia del circuito, ya sea
a través de la ley de ohm y luego de la ley de watt, o bien
aplicando alguna de las igualdades obtenidas
anteriormente.

33. RELACIONES QUE SE PUEDEN ESTABLECER
ENTRE LAS LEYES DE OHM Y WATT
P=IE
P = I x 1,5 V
I = E/R
I = 1,5 V / 10 Ω
I = 0,15 A
P = 0,15 A x 1,5 V
P = 0,225 W
P = 225 mW

34. RELACIONES QUE SE PUEDEN ESTABLECER
ENTRE LAS LEYES DE OHM Y WATT
Si queremos hacerlo directamente, buscamos la
ecuación en la cual se encuentre la E y la R, por ser los
valores que conocemos:
 P = E² / R
 P = 1,5² V / 10 Ω
 P = 2,25 V / 10 Ω
 P = 0,225 W
 P = 225 mW