Este documento presenta el capítulo 1 de un libro de física sobre el estudio de las ondas. El capítulo introduce conceptos clave como el movimiento armónico simple, el período y la frecuencia de un cuerpo vibrante, y define las ondas longitudinales y transversales. También explica conceptos como la amplitud, desplazamiento, resonancia, longitud de onda y el efecto Doppler. El objetivo es que los estudiantes comprendan los fundamentos físicos de las ondas y puedan aplicar estas nociones a problemas relacionados.






































![9.- Calcular la frecuencia de un rayo de luz de cualquier co
lor, conociendo su longitud de onda.
PROCEDIMIENTO.
1.- Realiza una lectura en forma general del capítulo III,
para que sepas el tema a tratar.
2.- Subraya lo más importante del capítulo.
3.- Extracta las definiciones y analízalas ampliamente.
4.- Realiza un resumen del capítulo.
5.- Escribe en una cartulina las ecuaciones de: la ilumina-
ción, índice de refracción y longitud de onda.
6 - Analiza detenidamente los problemas resueltos del capítu
lo y resuelve los que están en la autoevaluacion.
NOTA:
Es pre-requisito entregar completamente resueltos los
problemas nones de la autoevaluación del capítulo III en ho3as
tamaño carta.
CAPÍTULO III.
ESTUDIO DE LA LUZ.
.>-1 PROPAGACIÓN RECTILÍNEA DE LA LUZ.
La luz se propaga rectilíneamente; el hecho de que lns
ohiPt-ns nnpdan nrnrtnrir n»rf j ] ñdas es una d*mn.
f r a p i n n rTIIP
v y j ^ "en líneas rectas" v este PS
otro modo de definir la ofwuanae¿6n. M.cXjjJUnQjCL de la luz.
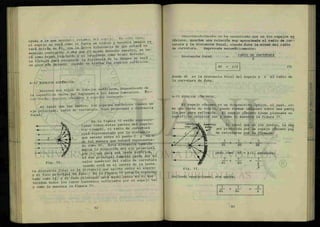
Cuando^se pone una figura o silueta delante de una fuen
te de luz, ésta producirá una sombra que será el contorno de
la silueta o figura que se ponga, tal y como lo muestra la
figura 1.
Si la pantalla se retira, la ima-
gen aumentará de tamaño mientras que si
se acerca, la imagen producida dismi- -
nuirá hasta casi quedar del tamaño ori-
ginal .
Cuando alejamos la pantalla n o t a —
mos que la imagen producida en ésta no
es tan nítida como cuando está cerca de
la imagen, esto se debe a que al alejar
la pantalla aparecen dos regiones muy
definidas, una región muy obscura llama
da tombía y la otra que está en los con
tornos de la snmhra y que se 1g T I a ^
Fig. 1
3-2 INTENSIDAD LUMINOSA
Un término muy empleado para especificar la luz total
emitida por una lámpara, es la buiía. Esta es una unidad
que usan los científicos como medida d» l . m i n n . i ^ ~ « n t n -
1020115814
51](https://image.slidesharecdn.com/librofisica-200915235401/85/Librofisica-40-320.jpg)






































![l o 1.5Volts o=
-i ^r ^ %+ f ~ +T~ ± L
l o 1.5 Voltsc^
Fig. 14-A.
Pig. 14.
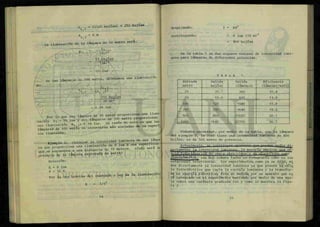
F = 1 . 5 V/celda x 4 celdas
total
= 6 volts.
dad.
Se tienen otras fuentes, tales como los acumuladores de
los automóviles (celdas de plomo y ácido), las foto-celdas
(transforman ]a luz en corriente eléctrica), termopares (ener
gía calorífica en corriente eléctrica) y el origen de la ~
electricidad por medio de la distorsión mecánica de un cris-
tal, efecto piezo eléctrico. Y las fuentes más importantes
la transformación de energía mecánica en eléctrica, por m e —
dio del dínamo y el generador.
5-9 GENERADORES.
Si la electricidad produce magnetismo, ¿podrá el magne-
tismo producir electricidad? Gracias a las investigaciones
y descubrimientos del Sr. Michael Faraday, se desarrolló el
dinamo eléctrico.
Con el fin de producir una corriente eléctrica, debe
existir un campo magnético, un conductor y movimiento relati
vo entre el campo y el conductor. Un gen&iadoA es un dispo"
sitivo que transforma la energía mecánica en eléctrica. El
método más conveniente y práctico para producir un movimien-
to relativo entre un campo magnético y un conductor, es sus-
pender una bobina giratoria dentro del campo. A dicha bobi-
na se le llama OAmadtlAa del generador.
Fig. 15.
En cada caso (fig. 15), la corriente inducida en el con
ductor forma un campo magnético en torno a él, que se opone""
al campo fijo o es repelida por éste. Esta oposición al con
ductor en movimiento debe de existir y es preciso aplicar
una forma de fuerza mecánica para vencer esa oposición. En
las grandes centrales de energía eléctrica se utiliza la - -](https://image.slidesharecdn.com/librofisica-200915235401/85/Librofisica-82-320.jpg)









![Cabe señalar, que la corriente en un circuito serie,
siempre tendrá el mismo valor para cada una de las resisten-
cias; mientras que en un circuito paralelo la corriente v a -
ría. El voltaje en un circuito serie varía en cada resisten
cia] mientras que en un circuito paralelo el voltaje permane
ce constante.
V = Vah = Vbg = Vcf = Vde.
T
0-5 SEGUNDA LEY DE KIRCHHOFF.
La segunda ley de Kirghhnf establece que la
dous los covUente* que ¿luyen hacia cualquier punto deuruón
e¿ igual a la suma de. todas la* coinievitdA que Jpygñ Mcar
asuena del mismo.
de Kirchoff, tenemos:
Nodo a Ii = 12 + I«» Nodo e in = 112
Nodo b I«f = 15 + I 7 Nodo f 19 = 112 + 18
Nodo c 17 = 18 + lio Nodo q 16 = 19 + 15
Nodo d Il OF Il 1 Nodo h 13 = 16 + 12
Pero si conocemos el voltaje de la fuente y sabiendo
que en cada resistencia existe el mismo voltaje podemos cal
cular la corriente que circula por cada una de las resisten
cias. Para la figura 13, tenemos:
IX = Vah/Ri= Vt/R1 i8 = V cf/R3 = VT /R3
I 5 = V b g / R 2 = V t / R 2 I U = Vde/Rj* = Vt/RI»
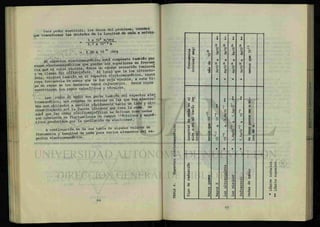
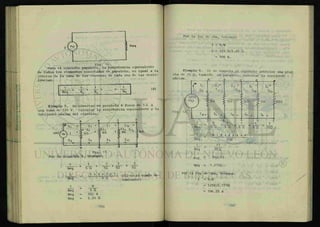
Ejemplo 7. De la figura 4, calcular la corriente que
circula por cada uno de los alambres.
112=
125 V/5fí = 25 A
I» = 125 V/5ft = 25 A
Fig. 14. • '
En el circuito mostrado en la fig. 12, tenemos:
I U = 125 V/5Í2 = 25 A
I13 = 125 V/5fl = 25 A
I15 = 125 V/20Í2= 6.25 A
Nodo e I5 = I15 = 6.25 A
Nodo f I6 = lis = 6.25 A
I5 + I m = 6.25 A + 25 A = 31.25 A
I6 + = 6.25 A + 25 A = 31.25 A
I„ + I 1 3 = 31.25 A + 25 A = 56.25 A
I7 + I 1 3 = 31.25 A + 25 A = 56.25 A
I3 + 112 = 56.25 A + 25 A = 81.25 A
Nodo d
Nodo g I
Nodo c
Nodo h le
Nodo b I2
7 =
=](https://image.slidesharecdn.com/librofisica-200915235401/85/Librofisica-93-320.jpg)