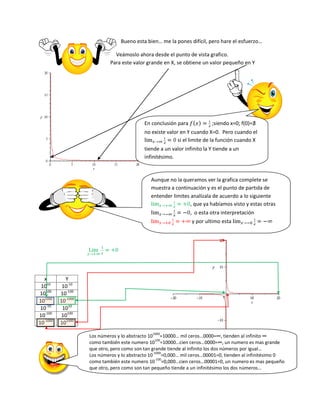
El documento explica los conceptos fundamentales de límite de una función. En particular, 1) un límite indica la tendencia o proximidad de los valores de una función cuando el valor de la variable se aproxima a cierto número; 2) para valores exactos de la variable se obtienen valores exactos de la función, mientras que para valores próximos de la variable se obtienen valores próximos de la función; y 3) las indeterminaciones surgen cuando el numerador y denominador tienden al mismo valor infinito o infinitésimo y no se sabe hacia dónde tiende la función.

1. Limite de una función
Recopilado por:
Pedro Orlando González Cordero
Licenciado en Educación Mención Física y Matemática
Entender el límite es una noción abstracta que indica tendencia o proximidad, pareciera que su
comportamiento es idéntico al de la función, y a decir verdad se parecen y genera la creencia de
confundir el límite con la función, esta creencia es errónea… Me explicare mas adelante
Si tenemos una función lineal pero como ejemplo
pero varios valores de x=1; x=2; x=3 los valores sustituidos en la función serán
=5; ; ; es decir que esta
función lineal para x=1 tendrá y=5; para x=2 tendrá y=8; para x=3 tendrá y=11;
quedaran los puntos P(x,y); P1(1,5); P2(2,8) y P3(3,11). En conclusión para valores
exactos de X se obtiene valores exactos de Y. Eso lo sabíamos verdad je je je
Pero en limite pasa algo parecido, es una tendencia por ejemplo para valores
próximos de X de la función se obtendrán valores próximos de Y por ejemplo
usemos la notación pareciese lo mismo que la función
pero se lee que cuando X se aproxima a 1 el valor de Y se aproxima a 5,
Pareciesen muy parecidos pero con el ejemplo que sigue estableceré lo distinto
Veamos para la función ; para el valor x=0; el valor de “y” no existe.
Veamos la tabla de la misma función
x Y En la medida que el valor crece en X de manera grotescamente el
1010 10-10 valor de Y lo hará de la misma manera decreciendo, léase
10100 10-100 matemáticamente mientras X tiende a infinito, es decir, se hace infinitamente grande
101000 10-1000 el valor de Y se hace infinitamente pequeño, cuando ocurre esto ultimo para reflejar
un numero que tiende a cero “0” se le dice infinitésimo
Epale amigo… tu me crees extraterrestre para entender
eso… Me puedes explicar de otra manera… porque no
entendí ni una papa...

2. Bueno esta bien… me la pones difícil, pero hare el esfuerzo…
Veámoslo ahora desde el punto de vista grafico.
Para este valor grande en X, se obtiene un valor pequeño en Y
En conclusión para ;siendo x=0; f(0)=
no existe valor en Y cuando X=0. Pero cuando el
si el limite de la función cuando X
tiende a un valor infinito la Y tiende a un
infinitésimo.
Aunque no la queramos ver la grafica complete se
muestra a continuación y es el punto de partida de
entender limites analízala de acuerdo a lo siguiente
, que ya habíamos visto y estas otras
, o esta otra interpretación
y por ultimo esta
x Y
1010 10-10
10100 10-100
101000 10-1000
10-10 1010
10-100 10100
10-1000 101000
Los números y lo abstracto 101000=10000… mil ceros…0000=∞, tienden al infinito ∞
como también este numero 10100=10000…cien ceros…0000=∞, un numero es mas grande
que otro, pero como son tan grande tiende al infinito los dos números por igual…
Los números y lo abstracto 10-1000=0,000… mil ceros…00001=0, tienden al infinitésimo 0
como también este numero 10-100=0,000…cien ceros…00001=0, un numero es mas pequeño
que otro, pero como son tan pequeño tiende a un infinitésimo los dos números…

3. Creo entender esto de lo “abstracto”… un número como otro es
tan grande que tienden al infinito “∞”; y como esto son los
números pequeños o infinitésimos “0”¿existirán otras cosas más
abstracto?
Recordemos las propiedades de los números de igual base y diferente potencia
Multiplicación de igual base ; División de igual base
Las indeterminaciones es otra cosa que se puede decir que se pide abstracción.
¿Qué es una indeterminación?
Esto enfrenta la posibilidad de un número pequeño en
comparación a otro, explicare este advenimiento, ¿Quién es más pequeño el
denominador o el numerador?:
a) = =0 esto tiende a un
infinitésimo
b) = =∞ esto tiende a un infinito
Entrando en comparación el numero resultante de (a) tiende a un infinitésimo mientras
el de (b) tiende a infinito… he aquí cuando se llega a una indeterminación porque no se
sabe hacia donde tiende a infinito o infinitésimo.
¿Debe haber solución para las indeterminaciones?
¿Existe la posibilidad de romper las
indeterminaciones?
Recordemos primero las factorizaciones y los productos notables:
a)
b)
c)
d)
e)
Debes recordarlas muy bien
como
vemos con asombro que al simplificar x – 1 del numerador y el
denominador es el termino que hace la indeterminación, porque lo anula
ambos términos. Este tipo de indeterminación no es la única, es a mi
parecer la mas común, existen otras indeterminaciones, se presenta a
continuación.

4. Solo se tomaran las dos
primeras indeterminaciones
Hagamos algunos ejercicios de :
a)
b)
c)
Veamos los tres casos de y su resolución recordando son
casos generales:
Los casos (a) polinomios numerador mayor grado que denominador, el (b) polinomios
numerador menor grado que denominador y el (c) polinomios de igual grado
a)
b)
c)
Chistes
¿Por qué se suicidó el libro de matemáticas?
Porque tenía muchos problemas. Eso fue
realmente malo
Claro, claro el
infinito ∞ es un
Si la respuesta del limite es 8 volteado y
¿Cuánto resulta el limite ? por eso
La respuesta es Ja Ja Ja volteaste el 5,
5
otro chiste
malo