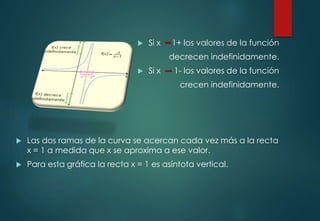
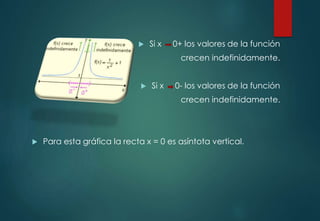
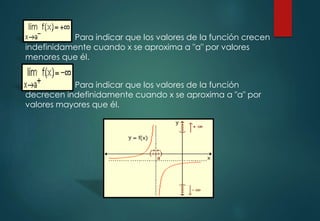
El documento explica los conceptos de límites infinitos y límites al infinito en matemáticas. Describe cómo una función puede crecer o decrecer indefinidamente a medida que su variable se aproxima a cierto valor o crece sin límite, y cómo esto se representa simbólicamente. También analiza el comportamiento de funciones con estos tipos de límites y proporciona ejemplos.

2. Límite de una Función
 El límite de una función es un concepto fundamental
del análisis matemático, un caso de límite aplicado a
las funciones.
 Intuitivamente, el hecho que una función f alcance
un límite L en el punto c, significa que el valor de f
puede ser tan cercano a L como se desee, tomando
puntos suficientemente próximos a c, sin importar el
valor que pudiera adquirir f en el punto c.

3. Límites Infinitos
Infinito, la palabra aparece regularmente en los conceptos
Matemáticos, esta es básicamente sólo una idea y no un
número. Una cantidad extremadamente grande la cual no
está definida puede ser considerada como infinito. Cuando
se calcula el límite de una fracción, en la que el numerador
se acerca a una cantidad positiva o negativa, si el
denominador se mueve hacia 0, entonces en ese caso se
dice que el límite es inexistente. Con el fin de explicar el
comportamiento de tales funciones, decimos que
 Esto indica que el límite de F® es un número desconocido
de gran tamaño. Este tipo de límites es conocido como
Límite Infinito. Los límites infinitos significan básicamente
que el límite es imaginario, es decir, el valor de la función
se puede hacer tan grande como queramos tomando los
valores de r suficientemente cerca de 0.

4.  Por ejemplo: una función x = 3y tiene límites infinitos. A
medida que y aumenta, 3y también aumenta y cuando y
se acerca al infinito, el límite de 3y se vuelve infinito.
 Además la definición de límite infinito puede ser girada
para un límite de un solo lado. El grafico correspondiente
de la función g(x) = que también posee límites infinitos
puede ser dibujada como:
 x −1 −0.1 −0.01 −0.001 0 g(x) 1 10010,000
1,000,000 indefinido

5. Maneras de analizar una grafica de limites
infinitos
 Si x 0+ los valores de la función
crecen indefinidamente.
 Si x 0- los valores de la función
decrecen indefinidamente
 Las dos ramas de la curva se acercan cada vez más al eje y a
medida que x se aproxima a cero.
 Para esta gráfica la recta x = 0 es asíntota vertical.

6.  Si x 1+ los valores de la función
decrecen indefinidamente.
 Si x 1- los valores de la función
crecen indefinidamente.
 Las dos ramas de la curva se acercan cada vez más a la recta
x = 1 a medida que x se aproxima a ese valor.
 Para esta gráfica la recta x = 1 es asíntota vertical.

7.  Si x 0+ los valores de la función
crecen indefinidamente.
 Si x 0- los valores de la función
crecen indefinidamente.
 Para esta gráfica la recta x = 0 es asíntota vertical.

8.  Si x 0+ los valores de la función
 Decrecen indefinidamente.
 Si x 0- los valores de la función
 Decrecen indefinidamente.
 Para esta gráfica la recta x = 0 es asíntota vertical

9.  El comportamiento de estas funciones no puede
describirse con la idea y el concepto de límite que se
ha estudiado hasta ahora.
 Analizando nuevamente la función y = ,se observa
en la gráfica que cuando x ® 0+, los valores de f
crecen más allá de todo tope. Por lo tanto f no tiene
límite cuando x ® 0+. Sin embargo resulta conveniente
decir que f(x) se aproxima a ¥ cuando x ® 0+. Se
escribe
 Esto no significa que el límite existe ni que +¥ es un
número real, sino que expresa que la función se hace
tan grande como deseamos escogiendo x
suficientemente cercano a cero.

10. Para indicar que los valores de la función
crecen indefinidamente(sin tope) cuando x se acerca a "a"
por izquierda y por derecha.
Para indicar que los valores de la función
decrecen indefinidamente (sin tope) cuando x se aproxima
a "a" por valores menores y mayores que él.

11. Para indicar que los valores de la función crecen
indefinidamente cuando x se aproxima a "a" por valores
menores que él.
Para indicar que los valores de la función
decrecen indefinidamente cuando x se aproxima a "a" por
valores mayores que él.

12. Para indicar que los valores de la función
decrecen indefinidamente cuando x se acerca a "a" por
valores menores que él.
Para indicar que los valores de la función
crecen indefinidamente cuando x se acerca a "a" por valores
mayores que él.

13. Limites en el infinito
Un concepto casi similar es el de “limites al infinito”. En este
cuando la función de una variable y aumenta
ilimitadamente entonces esta es mostrada como:
De manera similar, cuando y cae de manera ilimitada,
entonces esta es mostrada como:
 El concepto principal de límites al infinito yace en dos
puntos.
 1). Cuando k es un número no negativo, entonces
 2). Cuando k es un número no negativo, entonces

14.  Encontrar el límite de un número racional al infinito es un caso
especial en este concepto. Una regla sencilla para determinar el
límite al infinito de tales números es considerando la variable, tanto
en el numerador y en el denominador, que tenga el mayor
exponente. Ahora bien, los límites pueden ser evaluados en base a
las siguientes reglas:
 1). Si el numerador con el más alto exponente va junto al
denominador con el más alto exponente, en ese caso, el limite al
infinito y el infinito negativo es la proporción de ambos coeficientes
de mayor término.
 2). Al dividir el numerador con el denominador, si el exponente
resultante en la variable queda igual, en ese caso, el límite al infinito
y el infinito negativo son infinitos. Si resulta impar, en ese caso, el
límite al infinito es infinito y el infinito negativo es infinito negativo. Sin
embargo, en ambas condiciones, el numerador debe tener el
término más alto.
 3). En la fracción impropia, es decir, en la cual el denominador
contiene el término más alto, el límite al infinito y el infinito negativo
es 0.

15.  Los límites infinitos siguen unas propiedades importantes al
infinito, las cuales son:
 1). . En caso, que r sea grande, entonces el
recíproco de r será extremadamente pequeño y en el
caso que r aumente rápidamente, entonces disminuirá
en una proporción igual y eventualmente llegará cerca
de 0.
 2). Del mismo modo, si r se convierte grandemente
negativo, , se convertirá menos negativo y también se
aproximará más a 0.
 3). Además, un ejemplo similar ocurre cuando r es elevado
a algún exponente, es decir,

16. Comportamiento de funciones que crecen
o decrecen indefinidamente cuando la
variable también crece o decrece sin tope
f(x) Crece indefinidamente
a medida que x crece indefinidamente.
f(x) Crece indefinidamente
a medida que x decrece indefinidamente
f(x) Decrece indefinidamente a medida
que x crece indefinidamente.
f(x) Decrece indefinidamente a medida
que x decrece indefinidamente

17. f(x) crece indefinidamente a medida
que x crece indefinidamente.
f(x) decrece indefinidamente a medida
que x decrece indefinidamente
f(x) crece indefinidamente a medida
que x decrece indefinidamente.
f(x) decrece indefinidamente a medida
que x crece indefinidamente.

18. Estas funciones presentan comportamientos que no pueden
describirse con la idea y el concepto de límite estudiado. Por
lo tanto, debe extenderse dicho concepto para interpretar y
simbolizar estas situaciones.
Para indicar que la función decrece
indefinidamente cuando la variable crece indefinidamente.
Para indicar que la función crece
indefinidamente cuando la variable decrece
indefinidamente.

19. para indicar que la función
decrece indefinidamente cuando la variable decrece.
para indicar que la función
crece indefinidamente cuando la variable crece