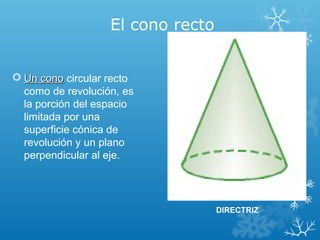
El documento describe los tipos de conos, incluyendo conos oblicuos y conos rectos. Explica los elementos básicos de un cono como la altura, el radio, la generatriz y la base. Luego detalla cómo calcular el área basal, el área lateral y el área total de un cono, proporcionando fórmulas y ejemplos numéricos.

1. ÁREA LATERAL Y
TOTAL DE UN CONO

2. TIPOS DE CONOS
 CONO OBLICUO:
Un cono oblicuo es el
cuerpo geométrico
resultante de cortar un
cono recto mediante un
plano oblicuo a su eje y
que corte a todas sus
generatrices.
 CONO RECTO O
CONO DE
REVOLUCIÓN:
….

3. El cono recto
V
 Un cono circular recto
como de revolución, es
la porción del espacio
limitada por una
superficie cónica de
revolución y un plano
perpendicular al eje.
A
O
DIRECTRIZ

5. Elementos básicos del cono
A
g
h
B
r
 Altura: es el segmento
AB que sale de la
cúspide del cono en
forma perpendicular a
la base del cono.
 Radio: el radio r, del
cono es le radio del
circulo que representa
la base del cono. (BC)
 Generatriz: la
generatriz g, del cono
es el segmento AC, que
al hacerse girar
C alrededor del AB
bordeando la
circunferencia, genera
el área lateral del cono.
 Base: la base del cono
es el círculo de centro B
y de radio r.

6. ÁREA BASAL
Es importante aclarar
que el área del cono
corresponde a la única
base que posee (área
del círculo)
π • r2
r

7. ÁREA LATERAL:
Corresponde a la superficie
curva que se produce al girar
la generatriz g, en torno al
eje y bordeando la base del
cono.
El área lateral del cono,
corresponde al área del
sector circular formado al
extender y desplegar, la
superficie curva a través de
su generatriz “g”.
ÁREA LATERAL

8. EjEmplo 1
Encuentre el área lateral de un cono circular recto si el radio de la base
mide 22cm y la generatriz 8cm.
8cm
AL = π • r • g
22cm
AL = π • 22cm • 8cm = 176πcm = 552,64cm
2
2

9. ÁREA TOTAL DE UN CONO
AT = AL + AB = ( π • r • g ) + ( π • r ) = π • r ( g + r )
AT = π • r ( g + r )

10. EjEmplo 2
Encuentre el área total de un cono si el radio de la base mide 6m y la
altura 9m.
g = h +r
2
2
2
g = 10,82 A = π • r ( g + r )
T
9cm
AT = π • 6 • (3 13 + 6)m
6cm
AT = 316,89m
2
2

11. EjEmplo 3
Encuentre el volumen de un cono si la base tiene como medida para su radio
12cm y la altura del sólido es 20cm.
1
2
V = •π • r h
3
1
2
3
V = • 12 • 20cm
3
Calculadora
V = 960πcm = 3014,4cm
3
3