Este documento presenta una introducción a las variables aleatorias y las distribuciones de probabilidad discretas y continuas más comunes utilizando el lenguaje R. En la sección 3, se explica la variabilidad a corto y largo plazo de las variables aleatorias y se simulan experimentos aleatorios como el problema del aniversario y los dados de Galileo. La sección 4 describe las distribuciones binomial, de Poisson y normal, y muestra cómo calcular probabilidades y generar muestras aleatorias para cada una en R. Finalmente, la sección 5 presenta ejemplos de

1. Pr´acticas de Estad´ıstica con R
Parte II
Escuela T´ecnica Superior
Ing. Industrial y Qu´ımica
Universidad de Cantabria
Fco Javier Glez Ortiz
Curso 2007–2008

2. 2

3. ´Indice general
3. Variables aleatorias 5
3.1. Variabilidad a corto plazo. Regularidad a la larga . . . . . . . . . . . . . . . . . . . . 5
3.1.1. Variabilidad a corto plazo: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
3.1.2. Variabilidad a largo plazo: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3.1.3. Concepto frecuentista de la probabilidad . . . . . . . . . . . . . . . . . . . . . 8
3.1.4. ¿Es siempre admisible el concepto cl´asico de probabilidad? . . . . . . . . . . 8
3.2. Simulaci´on del problema del aniversario . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.3. Simulaci´on del problema de los dados de Galileo . . . . . . . . . . . . . . . . . . . . 10
4. Distribuciones discretas y continuas 11
4.1. Distribuciones de probabilidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4.1.1. Binomial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4.1.2. Poisson . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.1.3. Normal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.2. Distribuci´on de la media muestral . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
5. Bondad de Ajuste 17
5.1. Contraste Chi-cuadrado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
5.1.1. ¿Es un dado regular? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
5.1.2. Bombardeo de Londres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
5.2. Contraste de Shapiro-Wilk . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
5.3. Contraste de Kolmogorov-Smirnov . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
5.3.1. Contraste de normalidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
5.4. Mas ejemplos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
7. Intervalos de confianza y contrastes de hip´otesis 21
7.1. Intervalo de confianza de la media. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
7.2. Intervalos de confianza y contraste de la proporci´on. . . . . . . . . . . . . . . . . . . 24
3

4. 4 ´INDICE GENERAL
7.3. Intervalos de confianza y contraste de diferencia de dos medias: . . . . . . . . . . . . 25
7.4. Intervalos de confianza y contraste de diferencia de dos proporciones. . . . . . . . . . 27

5. Tema 3
Variables aleatorias
3.1. Variabilidad a corto plazo. Regularidad a la larga
3.1.1. Variabilidad a corto plazo:
Simular 12 lanzamientos de un dado regular (no trucado), almacenando los resultados de los
lanzamientos en la columna 1 (”dado_1”).
Repetir el apartado anterior almacenando los resultados en la columna 2 (”dado_2”) y
(”dado_3”).
Dibujar diagramas de barras de los datos de las dos columnas.
>barplot(table(LosDados$dado3))
Calcular las frecuencias relativas de los 6 sucesos posibles. ¿Son estas frecuencias relativas
iguales a 1
6 ?
>table(LosDados$dado 3)/12
5

6. 6 TEMA 3. VARIABLES ALEATORIAS
1 2 3 4 5 6
0510152025
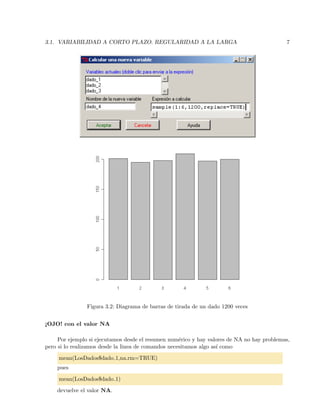
Figura 3.1: Diagrama de barras de tirada de un dado 120 veces
3.1.2. Variabilidad a largo plazo:
Simular 1200 lanzamientos de un dado regular (no trucado), almacenando los resultados de
los lanzamientos en la columna 4 (”dado_4”).
El entorno gr´afico nos impide obtener los 1200 datos, ¿como lo hacemos? Se puede entrar en
el editor y avanzar p´aginas hasta la fila de datos 1200, e introducir en esta casilla un NA.
Otra posibilidad desde la l´ınea de comandos, es escribir
LosDados[1200,] <- c(NA,NA,NA)
y a continuaci´on simular el lanzamiento del cuarto dado.
Y por supuesto lo m´as c´omodo ser´ıa abrir un nuevo data.frame
Repetir el apartado anterior almacenando los resultados en la columna 5 y 6 (”dado_5”) y
(”dado_6”).
Dibujar diagramas de barras de los datos de las dos columnas.
>barplot(table(LosDados$dado_4))
Calcular las frecuencias relativas de los 6 sucesos posibles. ¿Son estas frecuencias relativas
iguales a 1
6 ?

7. 3.1. VARIABILIDAD A CORTO PLAZO. REGULARIDAD A LA LARGA 7
Figura 3.2: Diagrama de barras de tirada de un dado 1200 veces
¡OJO! con el valor NA
Por ejemplo si ejecutamos desde el resumen num´erico y hay valores de NA no hay problemas,
pero si lo realizamos desde la linea de comandos necesitamos algo as´ı como
mean(LosDados$dado 1,na.rm=TRUE)
pues
mean(LosDados$dado 1)
devuelve el valor NA.

8. 8 TEMA 3. VARIABLES ALEATORIAS
Otra posibilidad para evitar los valores omitidos y poder calcular con datos que incluyen un
NA es,
x[!is.na(x)]
ya que, este comando elimina del vector x todos aquellos el mentos que sean NA o NaN. La
funci´on which(is.nan(x)) nos devolver´a las posiciones de los elementos de x que toman el valor
NaN.
3.1.3. Concepto frecuentista de la probabilidad
La concepci´on frecuentista interpreta que la probabilidad de un suceso es el l´ımite de la
frecuencia relativa de dicho suceso cuando el n´umero de veces que se repite el experimento asociado
tiende a infinito.
Por ejemplo, que la probabilidad de sacar cruz al tirar una moneda es 0,5 significa que, en una
sucesi´on de tiradas, la frecuencia relativa de las cruces obtenidas se ir aproximando paulatinamente
a 0,5 seg´un avanza la sucesi´on.
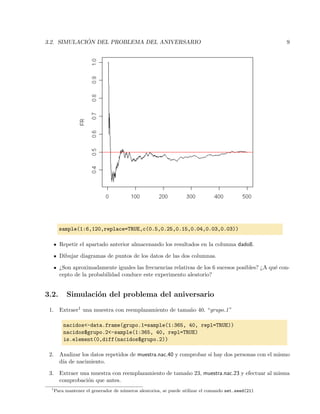
Generamos un vector que represente la sucesi´on de tiradas; suponiendo n = 500 tiradas.
dadoplot <- data.frame(caras=sample(c(0, 1), 500,replace=TRUE))
dadoplot$FA <- with(dadoplot, cumsum(caras))
plot (FR, type=’l’)
abline (0.5, 0, col=’red’)
Calculamos las frecuencias relativas de las cruces en cada tirada.
Representamos la secuencia de frecuencias relativas acumuladas.
Podemos a˜nadir la as´ıntota, a la altura del valor te´orico de la probabilidad p = 0,5
3.1.4. ¿Es siempre admisible el concepto cl´asico de probabilidad?
Simular 120 lanzamientos de un dado en cuyo interior se han introducido asim´etricamente bolas
de acero, de forma que P(1) = 0,5; P(2) = 0,25; P(3) = 0,15; P(4) = 0,04 y P(5) = P(6) = 0,03.
Almacenar los resultados de los lanzamientos en la variable dado7.

9. 3.2. SIMULACI ´ON DEL PROBLEMA DEL ANIVERSARIO 9
sample(1:6,120,replace=TRUE,c(0.5,0.25,0.15,0.04,0.03,0.03))
Repetir el apartado anterior almacenando los resultados en la columna dado8.
Dibujar diagramas de puntos de los datos de las dos columnas.
¿Son aproximadamente iguales las frecuencias relativas de los 6 sucesos posibles? ¿A qu´e con-
cepto de la probabilidad conduce este experimento aleatorio?
3.2. Simulaci´on del problema del aniversario
1. Extraer1 una muestra con reemplazamiento de tama˜no 40. “grupo.1”
nacidos<-data.frame(grupo.1=sample(1:365, 40, repl=TRUE))
nacidos$grupo.2<-sample(1:365, 40, repl=TRUE)
is.element(0,diff(nacidos$grupo.2))
2. Analizar los datos repetidos de muestra.nac.40 y comprobar si hay dos personas con el mismo
d´ıa de nacimiento.
3. Extraer una muestra con reemplazamiento de tama˜no 23, muestra.nac.23 y efectuar al misma
comprobaci´on que antes.
1
Para mantener el generador de n´umeros aleatorios, se puede utilizar el comando set.seed(21)

10. 10 TEMA 3. VARIABLES ALEATORIAS
3.3. Simulaci´on del problema de los dados de Galileo
1. Cargar un conjunto nuevo de datos en R. Simular el lanzamiento de un dado 1000 veces
variable dado.1
2. Realizar lo mismo para las columnas dado.2 y dado.3
3. Establecer en la columna suma, la suma de las tres dados.
4. Estimar la probabilidad de que la suma de los dados sea 10. 0.126
5. Estimar la probabilidad de que la suma de los dados sea 9. 0.118

11. Tema 4
Distribuciones discretas y continuas
4.1. Distribuciones de probabilidad
El men´u Distribuciones de R-Commander permite trabajar con todas las distribuciones es-
tad´ısticas vistas en clase de teor´ıa. Para cada una de ellas, se puede obtener:
Cuantil El menor valor c tal que, para un probabilidad dada p, se cumple que P(x ≤ c) = p
probabilidad Discretas: valores de la funci´on masa de probabilidad.
probabilidad acumulada Para un cuantil c dado, da el valor P(x ≤ c) (cola inferior) o bien
P(x > c) (cola superior).
gr´afico Se representa la funci´on de densidad (masa de probabilidad en las distribuciones discretas)
o la funci´on de distribuci´on.
muestra aleatoria Permite generar un juego de datos aleatorio especificando el n´umero de mues-
tras (n´umero de filas) y el tama˜no muestral (n´umero de columnas).
A cada uno de los nombres en R, se le a˜nade por delante la letra
d para funci´on de densidad (masa de probabilidad en discretas)
p para funci´on de distribuci´on
q para cuantil
r para generar n´umeros aleatorios
4.1.1. Binomial
pbinom(c(45), size=100, prob=0.5, lower.tail=TRUE)
1. Sea X ∼ B(p = 0,5, n = 100), np = 50, npq = 25. Hallar:
a) p(X ≤ 45), p(X ≤ 52) p(X < 60)
0.1841 0.6914 0.9716
11

12. 12 TEMA 4. DISTRIBUCIONES DISCRETAS Y CONTINUAS
b) Calcular las probabilidades anteriores con la aproximaci´on binomial-normal.
0.1841 0.6915 0.9713
c) Calcular las probabilidades anteriores con la aproximaci´on binomial-Poisson.
0.0 1 1
y analiza porqu´e es mala la aproximaci´on utilizada.
4.1.2. Poisson
P(X ≤ n) =
n
k=0
e−λ λk
k!
ppois(c(2), lambda=0.5, lower.tail=TRUE)
2. La centralita telef´onica de un hotel recibe un n´umero de llamadas por minuto que sigue una
ley de Poisson con par´ametro λ = 0,5. Determinar la probabilidad de que en un minuto al
azar:
a) Se reciba una ´unica llamada. 0.303
b) Se reciban un m´aximo de dos llamadas. 0.9856
c) La centralita quede bloqueada, sabiendo que no puede realizar m´as de 3 conexiones por
minuto. 0.00175
4.1.3. Normal
pnorm(c(40), mean=50, sd=5, lower.tail=TRUE)
3. Sea X una variable aleatoria normal con µ = 50 y σ2 = 25. Calcular:
a) p(X ≤ 40) p(X ≤ 60) p(X > 65)
0.02275 0.9772 0.0013
b) p(X > 35) p(40 < X < 60) p(30 < X < 42)
0.9986 0.9544 0.05476

13. 4.1. DISTRIBUCIONES DE PROBABILIDAD 13
Par´ametros de N(µ; σ)
Ejecutar en R el siguiente script y obervar el efecto del valor de los par´ametros.
x <- seq ( -6, 6, len=100 ) #%
y <- cbind ( dnorm ( x, -2, 1 ), dnorm (x, 0, 2 ), #%
dnorm ( x, 0, .5), dnorm ( x, 2, .3 ),#%
dnorm ( x, -.5, 3 ) )
matplot ( x, y, type="l", col=1 )
legend ( -6, 1.3, paste( "mu =", c(-2,0,0,2,-.5),"; sigma =",
c(1,2,.5,.3,3) ), lty=1:5, col=1, cex=.75 )
−6 −4 −2 0 2 4 6
0.00.20.40.60.81.01.2
x
y
mu = −2 ; sigma = 1
mu = 0 ; sigma = 2
mu = 0 ; sigma = 0.5
mu = 2 ; sigma = 0.3
mu = −0.5 ; sigma = 3

14. 14 TEMA 4. DISTRIBUCIONES DISCRETAS Y CONTINUAS
4.2. Distribuci´on de la media muestral
4. Abrir un fichero nuevo:
a) Abrimos un nuevo conjunto de datos o data.frame de nombre media.muestra y gener-
amos1 mediante muestreo aleatorio una muestra de tama˜no 100 de la variable Altura de
los alumnos de una poblaci´on con distribuci´on N(µ = 1, 75; σ = 0,05).
media.muestra<-data.frame(rnorm(100, mean=1.75, sd=0.05))
b) Generar de esta forma 25 columnas, lo que supone 25 muestras aleatorias de la variable
Altura.
media.muestra<-data.frame(media.muestra,matrix(rnorm(2500,1.75,0.05),ncol =25))
c) Calcular las medias de las columnas C1-C25 y representarlas en un gr´afico de puntos
entre los valores 1.73 y 1.77
apply(media.muestra,2,mean)
plot(apply(media.muestra,2,mean),ylim = c(1.73, 1.77))
abline(1.75,0,col=red”)
x ≈ 1.749595
d) Calcular las desviaciones t´ıpicas de las columnas C1-C25 y representarlas en un gr´afico
de puntos entre los valores 0.04 y 0.06. Sx ≈ 0.04906891
e) Representa en diagramas de cajas las 15 primeras columnas.
f ) Calcular una nueva columna con el promedio de las columnas C1-C25. Dar a esta colum-
na el nombre de Media.n25
media.muestra$Media.n25 <- apply(media.muestra,1,mean)
g) Representar el diagrama de cajas para comparar las columnas 1, 2 y 3 junto con la nueva
variable Media.n25. ¿Que se aprecia frente a los histogramas anteriores?
h) Calcular la media x25 de esta columna Media.n25
i) ¿Qu´e se aprecia entre
x25 y x
j) Calcular la desviaci´on t´ıpica Sx25 de la variable Media.n25 0.00978171
k) ¿Qu´e se diferencia aprecia entre (redondear a 3 d´ıgitos)
SX 0.05 y Sx25 0.01
1
para que coincidan los resultados aleatorios fijamos la misma semilla con set.seed(27)

15. 4.2. DISTRIBUCI ´ON DE LA MEDIA MUESTRAL 15
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
X1 X2 X3 X4 X5 X6 X7 X8 X9 X11 X13 X15
1.61.71.81.9
N(1.75;0.05)
Figura 4.1: Diagrama de las 15 muestras de la altura N(1,75; 0,05)

16. 16 TEMA 4. DISTRIBUCIONES DISCRETAS Y CONTINUAS
q
q
q
qq
X1 X2 X3 Media.n25
1.601.651.701.751.801.851.90
N(1.75;0.05)
Figura 4.2: Boxplot de X1, X2 y X3 junto a x25

17. Tema 5
Bondad de Ajuste
En el caso de contrastes de normalidad, se recomienda el uso del test de Shapiro-Wilk para
muestras peque˜nas n ≤ 50, mientras que si las muestras son grandes es preferible utilizar el test de
Kolmogorov-Smirnov, salvo que los datos vengan dados en una distribuci´on de frecuencias en cuyo
caso emplearemos la distribuci´on χ2
5.1. Contraste Chi-cuadrado
La distancia χ2 entre la distribuci´on de frecuencias observada en la muestra y la distribuci´on
de probabilidad especificada por la hip´otesis nula se define como
χ2
=
k
i=1
(ni − npi)2
npi
=
k
i=1
(Oi − Ei)2
Ei
, (5.1)
donde n1, n2, . . . , nk son las frecuencias absolutas de los k posibles resultados y p1, p2, . . . , pk son
las probabilidades de dichos resultados si es cierta la hip´otesis nula.
5.1.1. ¿Es un dado regular?
Se lanza un dado 1200 veces y se obtienen los siguientes resultados:
Xi 1 2 3 4 5 6
Oi: frecuencia 175 215 220 190 170 230
1. Calcular el estad´ıstico de contraste χ2. χ2
g.l. 15.75
2. Hallar el nivel de significaci´on (P-valor) de la prueba y decidir si se acepta que el dado es
regular.
P-valor 0.007595
Abrimos un conjunto de datos nuevo con dos columnas. En frec almacenamos las frecuencias ob-
servadas y en prob las probabilidades te´oricas respectivas para cada cara del dado 1
6 .
17

18. 18 TEMA 5. BONDAD DE AJUSTE
>chisq.test(frec,p=prob)
Chi-squared test for given probabilities
data: frec X-squared = 15.75, df = 5, p-value = 0.007595
5.1.2. Bombardeo de Londres
Durante la Segunda Guerra Mundial se dividi´o el mapa de Londres en cuadr´ıculas de 1/4 km
y se cont´o el n´umero de bombas ca´ıdas en cada cuadr´ıcula durante un bombardeo alem´an. Los
resultados fueron:
x: Impactos en cuadr´ıcula 0 1 2 3 4 5
Oi: frecuencia 229 211 93 35 7 1
Se quiere contrastar la hip´otesis de que los datos siguen una distribuci´on de Poisson. Se pide:
1. Dise˜nar las columnas adecuadas que registren las frecuencias observadas y las esperadas.
lambda<-sum(fre*impac)/sum(fre)
Calculamos las probabilidades de Poisson con
londres$prob <- with(londres, round(dpois(0:5, lambda=0.9288194),4))
2. Calcular el estad´ıstico del contraste χ2.
>chisq.test(londres$fre.a[1:5],p=londres$prob[1:5])
data: londres$fre.a[1:5] X-squared = 1.0118, df = 4, p-value =0.908
3. Hallar el cuantil 0,95 de la distribuci´on χ2
g.l. y decidir si se acepta que los datos de la muestra
se ajustan a la distribuci´on te´orica.

19. 5.2. CONTRASTE DE SHAPIRO-WILK 19
5.2. Contraste de Shapiro-Wilk
Con Datos - Conjunto de datos en paquetes Leer conjunto de datos.. del paquete datasets
cargar el fichero de nombre trees.
1. Efectuar el contraste de normalidad para la variable volumen de madera Volumen.
Con Estad´ısticos Res´umenes. y Test de normalidad de Shapiro-Wilk. obtenemos
W 0.8876
Como el p-value = 0.003579 rechazamos que sea una distribuci´on normal.
2. Efectuar el contraste de normalidad para la variable logaritmo del volumen de madera Volu-
men.
Con Estad´ısticos Res´umenes. y Test de normalidad de Shapiro-Wilk. obtenemos para la
nueva variable log(Volume)
W 0.9643
Como el p-value = 0.3766 aceptamos que el logaritmo del volumen sea normal.
5.3. Contraste de Kolmogorov-Smirnov
5.3.1. Contraste de normalidad
Vamos a realizar el contraste de normalidad de la variable PESO del fichero pesoaltura.rdat.
Dado que el n´umero de individuos es grande, n = 100, se utilizar´a el test de Kolmogorov-
Smirnov.
1. Con Datos - Cargar conjunto de datos ... incorporamos el fichero pesoaltura.rdat en Rcom-
mander con el nombre de peso.altura.
2. Calculamos los estimadores de µ y σ
attach(peso.altura)
mean(PESO)
sd(PESO)
resultando x = 73,37 y s = 12,69.
3. A continuaci´on se contrastan las diferencias entre la funci´on de distribuci´on emp´ırica muestral
y la distribuci´on te´orica normal de par´ametros, N(73,37; 12,69). Para ello se emplear´a el
procedimiento ks.test.
ks.test(PESO,pnorm,73.37,12.69)
>ks.test(PESO,pnorm,73.37,12.69)
One-sample Kolmogorov-Smirnov test
data: PESO D = 0.136, p-value = 0.04939 alternative hypothesis: two-sided
En este caso y para un α = 0,05 se rechaza la hip´otesis de que los pesos sigan una distribuci´on
normal.

20. 20 TEMA 5. BONDAD DE AJUSTE
5.4. Mas ejemplos
1. Los siguientes datos corresponden a la duraci´on de diez pilas de cierta marca en cientos de
horas.
i 1 2 3 4 5 6 7 8 9 10
xi 0,023 0,406 0,538 1,267 2,343 2,563 3,334 3,491 5,088 5,587
Se quiere contrastar si la variable aleatoria duraci´on de vida de las pilas se ajusta a una
distribuci´on de tipo exponencial. Se pide:
a) Sabiendo que la funci´on de distribuci´on exponencial es FX(x) = 1 − e−α x, determinar
su expresi´on si α se estima con ˆα = ¯x−1.
ˆα 0.40584
b) Determinar la distancia de Kolmogorov. D 0.2136
c) Concluir si los datos se ajustan a la distribuci´on exponencial dada.

21. Tema 7
Intervalos de confianza y contrastes
de hip´otesis
7.1. Intervalo de confianza de la media.
44. Cargar (abrir) el conjunto de Datos ElPulso.rda. Se pide:
a) Calcular el intervalo de confianza para el peso medio de todos los individuos
con α = 0,05.
Para realizar el contraste de la media o hallar el intervalo de confianza, se elige en el
Men´u, Medias->Test para una muestra
21

22. 22 TEMA 7. INTERVALOS DE CONFIANZA Y CONTRASTES DE HIP ´OTESIS
t.test(Pulso$Peso, alternative=’two.sided’, mu=0.0, conf.level=.95)
One Sample t-test
data: Pulso$Peso t = 58.6473, df = 91, p-value <2.2e-16
alternative hypothesis: true mean is not equal to 0 95 percent confidence interval:
63.66709 68.13108
sample estimates: mean of x 65.89909
help(t.test)
b) Calcular el intervalo de confianza para el peso medio de las mujeres con
α = 0,05.
En este caso, si se quiere trabajar con el data.frame habr´ıa que crear una columna con
los pesos de las mujeres dejando NA para los pesos de los hombres. A continuaci´on se
proceder´ıa como en el apartado anterior.
Pero la forma m´as sencilla es recuperar el comando de t.test del apartado anterior e
indicarle la variable adecuada.
t.test(Peso[Sexo==’mujer’], alternative=’two.sided’, mu=0.0,
conf.level=.95)
intervalo 54.12-58.29
c) Estudios recientes afirman que la altura media de las mujeres de esta poblaci´on
es µ = 167 cm. A la vista de estos datos, ¿podemos aceptar dicha hip´otesis?
Como en el caso anterior para el intervalo, ahora indicamos el valor de µ a contrastar
mu=167
t.test(Altura[Sexo==’mujer’], alternative=’two.sided’,
mu=167, conf.level=.95)
p-value 0.4273
Se observa que el p-valor obtenido es superior al nivel de significaci´on fijado en α = 0,05,
luego aceptar´ıamos la hip´otesis.
d) Calcular el intervalo de confianza para el Pulso1 medio de las mujeres que no fuman.
t.test(Pulse1[Sexo==’mujer’ & Fumar==’no’],alternative=’two.sided’,
mu=0.0, conf.level=.95)
(70,36 − 78,83)
e) Calcular el intervalo de confianza para la media del incremento del pulso (Pulso2-Pulso1)
para los individuos que corrieron.
t.test(increpulso[Correr==’corrio’], alternative=’two.sided’,
mu=0.0, conf.level=.95)
(13,74 − 24,08)

23. 7.1. INTERVALO DE CONFIANZA DE LA MEDIA. 23
45. Se espera que la resistencia en kg/cm2 de cierto material suministrado por un proveedor se
distribuya normalmente, con media 220 y desviaci´on t´ıpica 7.75. Se toma una muestra de 9
elementos y se obtiene: 203, 229, 215, 220, 223, 233, 208, 228, 209. Se pide:
a) Contrastar la hip´otesis µ = 220 y σ cualquiera.
En la Ventana de instrucciones asignamos la variable resistencia con
resistencia <- c(203, 229, 215, 220, 223, 233, 208, 228, 209)
Como en el ejercicio anterior efectuamos el contraste t.test
t.test(resistencia,alternative=’two.sided’,mu=220,conf.level=.95)
Y obtenemos el resultado en la Ventana de resultados
————————————-
One Sample t-test
————————————-
data: resistencia$resis
t = -0.6665, df = 7, p-value =0.5265
alternative hypothesis: true mean is not equal to 220
95 percent confidence interval:
208.6298 226.3702
sample estimates: mean of x 217.5
b) Contrastar la hip´otesis σ = 7,75 y µ cualquiera.
Este contraste no aparece entre las opciones de Rcommander, por ello vamos a utilizar
las f´ormulas. Calculamos el estad´ıstico de contraste con
(n − 1)s2
X
σ2
∼ χ2
n−1
D <- (length(x)-1)*var(x)/7.75^2
Calculamos el nivel cr´ıtico (p-valor) de la distribuci´on, es decir, el ´area que queda
a la derecha de D, teniendo en cuenta que el estad´ıstico del contraste sigue una
Chi-cuadrado.
pchisq(D,length(x)-1, ncp=0, lower.tail = FALSE)%
Como p-value=0.06416552 aceptamos la hip´otesis nula si el nivel de significaci´on
es 0.05.

24. 24 TEMA 7. INTERVALOS DE CONFIANZA Y CONTRASTES DE HIP ´OTESIS
7.2. Intervalos de confianza y contraste de la proporci´on.
47. Cargar (abrir) el conjunto de Datos Pulso.rda y calcular el intervalo de confianza para
la proporci´on pF de individuos que fuman con α = 0,05.
Para realizar el contraste de la proporci´on o hallar el intervalo de confianza, se elige en el
Men´u, Proporciones->Test de Proporciones para una muestra
> .Table <- xtabs( Fumar , data= Pulsaciones )
>.Table Fumar
fuma no fuma
28 64
> prop.test(rbind(.Table), alternative=’two.sided’, p=.5, conf.level=.95, correct=FALSE)
1-sample proportions test without continuity correction
data: rbind(.Table), null probability 0.5
X-squared = 14.087, df = 1, p-value = 0.0001746 alternative hypothesis: true p is not
equal to 0.5 95 percent
confidence interval: 0.2197369 0.4046427 sample estimates: p 0.3043478
prop.test(c(28),c(92) alternative=’two.sided’, p=.5, conf.level=.95, correct=FALSE)

25. 7.3. INTERVALOS DE CONFIANZA Y CONTRASTE DE DIFERENCIA DE DOS MEDIAS:25
7.3. Intervalos de confianza y contraste de diferencia de dos
medias:
52. Cargar (abrir) el conjunto de Datos Pulso.rda y determinar si hay diferencia signi-
ficativa entre la altura media de hombres y mujeres con un nivel de significaci´on
α = 0,05.
Si llamamos a la altura media de hombres µH y a la altura media de mujeres µM , se trata de
realizar el contraste
H0 ≡ µH = µM = µ0
H1 ≡ µH = µM
Este ejercicio lo vamos a resolver de 2 formas.
La primera acudimos en el Men´u, a Medias->Test de para muestras indepeendientes. A
continuaci´on elegimos la variable explicada Altura desglosada por la variable de Grupos
Sexo, dejando por defecto la opci´on de contraste Bilateral y tambi´en por defecto no
suponer varianzas iguales (σ2
1 = σ2
2)
La salida en la Ventana de resultados nos dice que el p-value = 9.778e-15 muy inferior
que el α = 0,05 que hab´ıamos fijado. Por ello se rechaza la igualdad de medias. A su
vez, llegamos a la misma conclusi´on, si nos fijamos en que
confidence interval: 10.80570 16.39458, no incluye el valor nulo.

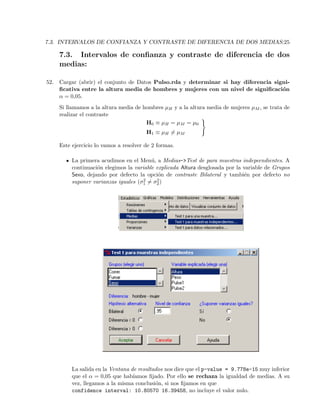
26. 26 TEMA 7. INTERVALOS DE CONFIANZA Y CONTRASTES DE HIP ´OTESIS
> t.test(Altura~Sexo, alternative=’two.sided’, conf.level=.95,
var.equal=FALSE, data=Pulsaciones)
Welch Two Sample t-test
data: Altura by Sexo t = 9.7007, df = 72.514, p-value = 9.778e-15
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
10.80570 16.39458
sample estimates: mean in group hombre mean in group mujer
179.7161 166.1160
El m´etodo anterior con men´us requiere tener los valores de las dos variables en una
misma columna y a su vez desglosada con otra columna que hace de factor. La segunda
forma es m´as vers´atil.
A partir del comando t.test de arriba bastar´ıa escribir:
t.test(Altura[Sexo==’hombre’],Altura[Sexo==’mujer’],
var.equal=FALSE, alternative=’two.sided’, conf.level=.95,
Teniendo en cuenta que la selecci´on de las variables puede ser m´as complicado que las opciones
que ofrece el Men´u de Rcommander, la segunda forma es m´as flexible que la primera.

27. 7.4. INTERVALOS DE CONFIANZA Y CONTRASTE DE DIFERENCIA DE DOS PROPORCIONES.27
7.4. Intervalos de confianza y contraste de diferencia de dos
proporciones.
52. Cargar (abrir) el conjunto de Datos Pulso.rda y determinar si hay diferencia signi-
ficativa entre la proporci´on de hombres y mujeres que fuman con un nivel de
significaci´on α = 0,05.
Si llamamos a la proporci´on de hombres que fuman pF|H y a la proporci´on de mujeres que
fuman pF|M , se trata de realizar el contraste
H0 ≡ pF|H = pF|M = p0
H1 ≡ pF|H = pF|M
Este ejercicio lo vamos a resolver de 2 formas.
La primera acudimos en el Men´u, a Proporciones->Test de Proporciones para dos mues-
tras. A continuaci´on elegimos la variable explicada Fumar desglosada por la variable de
Grupos Sexo, dejando por defecto la opci´on de contraste Bilateral y tambi´en por defecto
la aproximaci´on normal
La salida en la Ventana de resultados nos dice que el p-value = 0.2158 mayor que el
α = 0,05 que hab´ıamos fijado. Por ello se acepta la igualdad de proporciones. A su vez,

28. 28 TEMA 7. INTERVALOS DE CONFIANZA Y CONTRASTES DE HIP ´OTESIS
llegamos a la misma conclusi´on, si nos fijamos en que
confidence interval: -0.06398087 0.30859240, incluye el valor nulo,
> .Table <- xtabs(~Sexo+Fumar, data=Pulsaciones)
> rowPercents(.Table)
Fumar
Sexo fuma no fuma Total Count
hombre 35.1 64.9 100 57
mujer 22.9 77.1 100 35
> prop.test(.Table, alternative=’two.sided’, conf.level=.95, correct=FALSE)
2-sample test for equality of proportions without continuity correction
data: .Table X-squared = 1.5321, df = 1, p-value = 0.2158
alternative hypothesis: two.sided 95 percent confidence interval:
-0.06398087 0.30859240
sample estimates:
prop 1 prop 2
0.3508772 0.2285714
La segunda es hacer el recuento de las frecuencias respectivas, con:
x1<-sum(Sexo==’hombre’ & Fumar==’fuma’);n1<-sum(Sexo==’hombre’)
x2<-sum(Sexo==’mujer’ & Fumar==’fuma’);n2<-sum(Sexo==’mujer’)
prop.test(c(x1,x2),c(n1,n2), alternative=’two.sided’, conf.level=.95, correct=FALSE)
Teniendo en cuenta que el recuento de las variables puede ser m´as complicado que las opciones
que ofrece el Men´u de Rcommander, la segunda forma es m´as flexible que la primera.