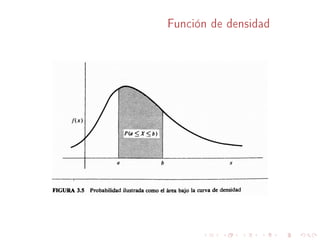
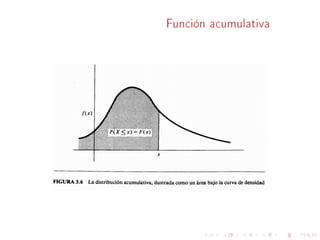
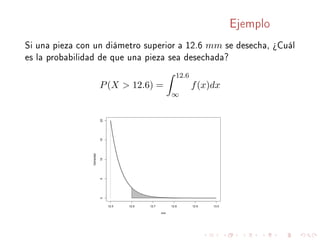
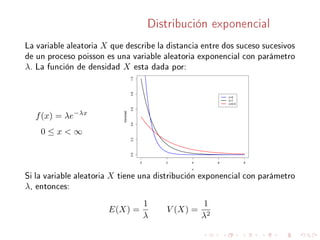
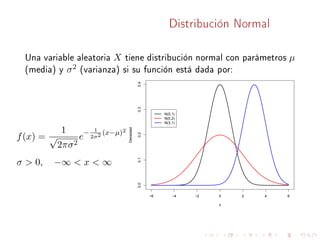
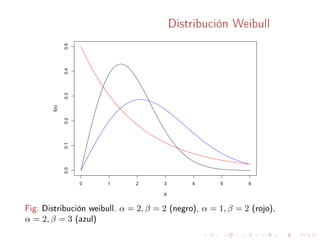
Este documento describe conceptos básicos sobre distribuciones de probabilidad para variables continuas. Explica que una variable aleatoria continua puede tomar cualquier valor real en un intervalo, y que su distribución de probabilidad se caracteriza por una función de densidad. También define conceptos como función de distribución acumulativa, valor esperado, varianza, y distribuciones como la exponencial, normal y Weibull.

1. Distribución de Probabilidad
Variables continuas
Álvaro José Flórez
1Escuela de Estadística
Facultad de Ingeniería
Febrero - Junio 2014

2. Variable aleatoria continua
Se dice que una variable aleatoria es continua si puede tomar cualquier
valor en un intervalo (números reales en un intervalo)
Si X es una variable aleatoria continua, la probabilidad de que la variable
tome un valor determinado siempre es cero.
Para el caso continuo se está interesado no en probabilidad de exactamente
un valor, sino en la probabilidad de que la variable aleatoria se encuentre
dentro de un intervalo.
La distribución de probabilidad de una v.a. continua está caracterizada
por una función (f(x)) llamada función de densidad, por medio de la cual
podemos calcular la probabilidad de un intervalo a ≤ X ≤ b.

3. Función de densidad
Sea X una variable aleatoria continua. Entonces una función de
densidad de X es una función f(x) tal que para dos números
cualesquiera a y b con a ≤ b,
P(a ≤ X ≤ b) =
b
a
f(x)dx
Es decir, la probabilidad de que X tome un valor en el intervalo (a,b)
es el área bajo la curva de la función de densidad. Además f(x) debe
cumplir:
f(x) ≥ 0
∞
−∞
f(x)dx = 1

4. Función de densidad

5. Función acumulativa
La función de distribución acumulativa de una v.a. continua X es la
probabilidad de que X tome un valor menor o igual a x. Esto es,
F(x) = P(X ≤ x) =
x
−∞
f(t)dt
dado que P(X = x) = 0, entonces P(X ≤ x) = P(X < x) =
F(x). Propiedades:
• F(−∞) = 0, F(∞) = 1
• F(a < X < b) = F(b) − F(a)
• dF(x)
dx = f(x)

6. Función acumulativa

7. Ejemplo
Sea X la variable aleatoria continua que denota el diámetro de un
oricio perforado en una pieza de un componente metálico. Los datos
históricos muestran que la distribución de X (en mm) puede ser
modelada por la siguiente función de densidad:
f(x) = 20e−20(x−12.5)
x ≥ 12.5
f(x) es una función de densidad pues: f(x) ≥ 0
∞
−∞ f(x)dx = 1

8. Ejemplo
Sea X la variable aleatoria continua que denota el diámetro de un
oricio perforado en una pieza de un componente metálico. Los datos
históricos muestran que la distribución de X (en mm) puede ser
modelada por la siguiente función de densidad:
f(x) = 20e−20(x−12.5)
x ≥ 12.5
f(x) es una función de densidad pues: f(x) ≥ 0
∞
−∞ f(x)dx = 1
Si una pieza con un diámetro superior a 12.6 mm se desecha, ¾Cuál
es la probabilidad de que una pieza sea desechada?

9. Ejemplo
Si una pieza con un diámetro superior a 12.6 mm se desecha, ¾Cuál
es la probabilidad de que una pieza sea desechada?
P(X 12.6) =
12.6
∞
f(x)dx
12.5 12.6 12.7 12.8 12.9 13.0
05101520
mm
Densidad

10. Valor esperado y varianza
Sea X una variable aleatoria continua con función de densidad f(x).
La media o el valor esperado de X, denotado como µ o E(X), es:
E(X) =
∞
−∞
xf(x)dx
La varianza de X, denotada como V (X) o σ2, es:
V (X) =
∞
−∞
(x − E(X))2
f(x)dx =
∞
−∞
x2
f(x)dx − E(X)2
La desviación estándar de X es igual a V (X)

11. Ejercicio
La resistencia de una muestra de un deteminado material viene dado
por una variable aleatoria X, con función de densidad,
f(x) =



x si 0 x ≤ 1
2x+1
8 si 1 x ≤ 2
0 en otro caso
• Si una muestra se encuentra en estado ideal de resistencia si
ésta se encuentra entre 0.5 y 1.5, ¾Cuál es la probabilidad de
que una muestra se encuentre en estado ideal?
• Calcule la esperanza y la varianza de la variable aleatoria X.

12. Percentiles de una distribución
Sea p un número entre 0 y 1. El percentil (100p) de la distribución
de una variable aleatoria X, está denido por:
F(x ) =
x
−∞
f(y)dy = p
x es el valor tal que P(X ≤ x ) = p.
La mediana (Me) de una distribución continua es el percentil 50, es
decir que satisface F(Me) = 0.5.
Los cuartiles, denotados por Q1, Q2 y Q3, de una distribución
corresponden a los percentiles 25, 50 y 75, respectivamente. Me =
Q2.

13. Distribuciones de probabilidad
En el caso continuo algunas distribuciones de probabilidad son:
• Exponencial
• Normal
• Weibull
• Uniforme
• Gamma

14. Distribución exponencial
La variable aleatoria X que describe la distancia entre dos suceso sucesivos
de un proceso poisson es una variable aleatoria exponencial con parámetro
λ. La función de densidad X esta dada por:
f(x) = λe−λx
0 ≤ x ∞
0 2 4 6 8
0.00.20.40.60.81.0
x
Densidad
λ=2
λ=1
λ=0.5
Si la variable aleatoria X tiene una distribución exponencial con parámetro
λ, entonces:
E(X) =
1
λ
V (X) =
1
λ2

15. Ejemplo
La amplia experiencia con ventiladores de cierto tipo utilizados en motores
diesel, indica que la distribución exponencial proporciona un buen modelo
para la variable aleatoria X el tiempo hasta que se presenta una falla.
Suponga que el valor espero de X es de 25.000 horas.
1 ¾Cuál es la probabilidad de que un ventilador seleccionado dure
entre 20.000 y 30.000 horas?
2 Los productores quieren determinar el tiempo de garantía de los
ventiladores teniendo en cuenta que están dispuestos a recibir por
garantía a no más del 15 % de los ventiladores producidos, ¾Cuál
debería ser el tiempo estipulado de garantía?
Suponga que el número de kilómetros que puede recorrer un automóvil
antes de que se le acabe la batería está distribuido exponencialmente con
un valor promedio de 10000km. Si una persona quiere realizr un viaje de
5000km, ¾Cuál es la probabilidad de que llegue al nal de su viaje sin tener
que cambiar la batería?

16. Ejercicio
Sea la variable aleatoria X el tiempo, en horas, necesario para reparar
una pieza de equipo, en un proceso de manufactura, es una variable
aleatoria exponencial con λ = 1/5.
1 Cuál es la probabilidad de que para reparar una pieza sea
necesario más de 5 horas.
2 Determinar los cuartiles de la variable X.
3 Si la perdida de dinero es igual al cuadrado del número de
horas necesarias para llevar a cabo la reparación, determine el
valor esperado de las pérdidas por reparación

17. Distribución Normal
La distribución normal es una de las distribuciones más importantes
y de uso más frecuente en la estadística, puesto que gran parte
de la teoría fue desarrollada inicialmente para variables con esta
distribución.
La gran mayoría de variables aleatorias que se estudian
en experimentos físicos (alturas, pesos) son aproximadamente
modelados por una distribución normal.
Muchas distribuciones de probabilidad, incluyendo discretas, pueden
ser aproximadas por esta distribución (si se cumplen ciertas
condiciones).
Aunque una variable no se distribuya normal, las sumas y promedios
de las variables, si se cumplen ciertas condiciones, tendrán una
distribución normal aproximada (Teorema Central del Límite)

18. Distribución Normal
Una variable aleatoria X tiene distribución normal con parámetros µ
(media) y σ2 (varianza) si su función está dada por:
f(x) =
1
√
2πσ2
e− 1
2σ2 (x−µ)2
σ 0, −∞ x ∞
−6 −4 −2 0 2 4 6
0.00.10.20.30.4
x
Densidad
N(0,1)
N(0,2)
N(3,1)

19. Ejemplo
La resistencia a la compresión de muestras de cemento puede ser
modelada por una distribución normal con media de 6000Kg/cm2
y una desviación estándar de 100Kg/cm2. ¾Cuál es la probabilidad
de que la resistencia a la compresión de una muestra sea inferior a
6250Kg/cm2?
P(X 6250) =
6250
−∞
1
2π(100)2
e
− 1
2(100)2 (x−6000)2
dx

20. Ejemplo
La resistencia a la compresión de muestras de cemento puede ser
modelada por una distribución normal con media de 6000Kg/cm2
y una desviación estándar de 100Kg/cm2. ¾Cuál es la probabilidad
de que la resistencia a la compresión de una muestra sea inferior a
6250Kg/cm2?
P(X 6250) =
6250
−∞
1
2π(100)2
e
− 1
2(100)2 (x−6000)2
dx
Ninguna de las técnicas estándar se pueden usar para evaluar la expresión
anterior. En vez de eso, para µ = 0 y σ = 1 (normal estándar) se han
evaluado numéricamente y tabulado ciertos valores. A partir de estas tablas
se puede usar para calcular probabilidades para cualquier µ y σ

21. Distribución normal
Si X tiene una distribución normal con media µ y desviación estándar
σ, entonces:
Z =
X − µ
σ
Tiene una distribución normal estándar. Así,
P(a ≤ X ≤ b) = P(
a − µ
σ
≤ Z ≤
b − µ
σ
)
= P(Z
b − µ
σ
) − P(Z
a − µ
σ
)
Al estandarizar, cualquier probabilidad en la que interviene X se
puede expresar como una probabilidad asociada a una variable
aleatoria Z (Normal Estándar)

22. Ejercicio
Una prestigiosa universidad de la región tiene como estrategia de
selección la aplicación de una prueba de conocimientos, sobre cuyos
resultados escoge al 20 % de los estudiantes, quienes deben tener
los mayores puntajes en dicho examen. Si las calicaciones de este
examen siguen una distribución normal con media 65 y desviación
estándar 20. Determine:
• La calicación mínima que debe obtener un estudiante para ser
seleccionado.
• Si se decide otorgar una beca a los estudiantes que presentan
un puntaje superior a 98 puntos, que proporción de estudiantes
serian becados?
• ¾Cuál es la probabilidad de que una calicación se encuentre
alejada de su media en mas de dos desviaciones estándar?

23. Ejemplo
Una empresa productora está interesada en conocer el gasto promedio
semanal en cierto tipo de alimento de las familias de estrato
socioeconómico medio, con el n de diseñar una estrategia de mercado
para promover la demanda en el mercado. Si se supone que el gasto
promedio semanal en cierto tipo de alimento de las familias de estrato
socioeconómico medio se distribuye Normal con media 61.73 y desviación
estándar 10.3.
¾Cuál es la probabilidad de que una familia gaste más de $75000 en ese
tipo de alimento?
Si la empresa quiere determinar el valor de su producto teniendo en
cuenta que mínimo el 60 % de la población tenga capacidad de comprarlo.
Basándose en la distribución de probabilidad de los datos ¾Cuál debería
ser el valor del nuevo producto?

24. Distribución Weibull
La distribución Weibull sirve para modelar tiempos de falla de
diferentes sistemas físicos, sobretodo cuando la probabilidad de que
un elemento falle cambia en el tiempo.
Una variable aleatoria X tiene una distribución Weibull si su función
de densidad es,
f(x) =
α
βα
xα−1
e
− x
β
α
Donde α 0 (parámetro de forma) y β 0 (parámetro de escala).
Su valor esperado y varianza es,
E(X) = βΓ 1 +
1
α
V (X) = β2
Γ 1 +
2
α
−β2
Γ 1 +
1
α
2

25. Distribución Weibull
0 1 2 3 4 5 6
0.00.10.20.30.40.5
X
f(x)
Fig: Distribución weibull. α = 2, β = 2 (negro), α = 1, β = 2 (rojo),
α = 2, β = 3 (azul)

26. Función Gamma
La función gamma está denida como:
Γ(r) =
∞
0
xr−1
e−x
dx, para r 0
Se puede demostrar que:
Γ(r) = (r − 1)Γ(r − 1)
Por lo tanto, si r es un entero positivo,
Γ(r) = (r − 1)!

27. Ejemplo
Si el tiempo de vida (en horas) de cierto componente expuesto a
gases corrosivos tiene una distribución de probabilidad con α = 3 y
β = 900. Entonces:
• Determine la vida media y la varianza del componente.
• ¾Cuál es la probabilidad de que el componente falle antes de
500?
• ¾Cuál es la probabilidad de que falle después de 700 horas?

28. Algunos ejercicios
El diámetro de un punto producido por una impresora se
distribuye normal con media de 0.0002 pulgadas. Suponga que las
especicaciones requieran que el diámetro del punto esté entre 0.0014
y 0.0026 pulgadas. Si la probabilidad de que un punto cumpla con
las especicaciones debe ser de 0.9973, Qué valor de la desviación
estándar es necesario?

29. Algunos ejercicios
El diámetro de un punto producido por una impresora se
distribuye normal con media de 0.0002 pulgadas. Suponga que las
especicaciones requieran que el diámetro del punto esté entre 0.0014
y 0.0026 pulgadas. Si la probabilidad de que un punto cumpla con
las especicaciones debe ser de 0.9973, Qué valor de la desviación
estándar es necesario?
La resistencia última (ksi) a -200 grados F de un tipo de acero que
exhibe fragilidad al frio a bajas temperaturas se puede modelar por
medio de una distribución Weibull con parámetros α = 20 y β = 100.
• ¾Cuál es la probabilidad de que el acero presente una
resistencia superior a 105 ksi?
• ¾Para qué valor X se encuentra el 10 % de las resistencias más
bajas?