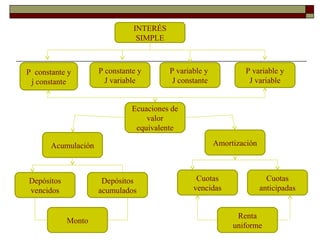
El documento presenta los objetivos y conceptos básicos de la matemática financiera. El objetivo principal del curso es que los estudiantes aprendan a aplicar el principio del valor del dinero en el tiempo a operaciones financieras, como calcular intereses simples cuando el principal y la tasa son constantes usando diferentes fórmulas. También define conceptos clave como tasa nominal, interés, principal, plazo y presenta ejemplos numéricos para ilustrar los cálculos.

1. Lic. Reneé Porras Pérez
Matemática Financiera
Welcome to the course of
financial mathematics

2. “Buscar que el estudiante,
al final del curso sea capaz
de plantear problemas y
efectuar cálculos aplicando
el principio del valor del
dinero en el tiempo, a las
operaciones que se
desarrollan en el sistema
financiero nacional”
“Buscar que el estudiante,
al final del curso sea capaz
de plantear problemas y
efectuar cálculos aplicando
el principio del valor del
dinero en el tiempo, a las
operaciones que se
desarrollan en el sistema
financiero nacional”
Objetivo del CursoObjetivo del Curso
Matemática FinancieraMatemática Financiera

3. La Matemática Financiera
es una derivación de la
matemática aplicada que
estudia el valor del dinero en
el tiempo, combinando el
capital, la tasa y el tiempo
para obtener un rendimiento
o interés, a través de
métodos de evaluación que
permiten tomar decisiones
de inversión.
La Matemática Financiera
es una derivación de la
matemática aplicada que
estudia el valor del dinero en
el tiempo, combinando el
capital, la tasa y el tiempo
para obtener un rendimiento
o interés, a través de
métodos de evaluación que
permiten tomar decisiones
de inversión.
DEFINICIÓN

4. La matemática financiera
es de aplicación
eminentemente práctica,
su estudio esta
íntimamente ligado a la
resolución de problemas
y ejercicios muy
semejantes a los de la
vida cotidiana, en el
mundo de los negocios.
Dinero y finanzas son
indesligables.
La matemática financiera
es de aplicación
eminentemente práctica,
su estudio esta
íntimamente ligado a la
resolución de problemas
y ejercicios muy
semejantes a los de la
vida cotidiana, en el
mundo de los negocios.
Dinero y finanzas son
indesligables.

6. Es el beneficio por
la colocación de un
capital
representado por
un stock (monto) de
efectivo
Es el beneficio por
la colocación de un
capital
representado por
un stock (monto) de
efectivo
El Interés
corresponde al
uso del uso del
capital ajeno
durante un
intervalo de
tiempo
determinado
El Interés
corresponde al
uso del uso del
capital ajeno
durante un
intervalo de
tiempo
determinado
Recíprocamente,
el costo que
asume el
prestatario por
usar ese capital
durante un
periodo de tiempo
temporal
Recíprocamente,
el costo que
asume el
prestatario por
usar ese capital
durante un
periodo de tiempo
temporal

7. uno el principal
(stock inicial)
uno el principal
(stock inicial) el otro el interésel otro el interés
Se conjugan dos elementos en el uso del dineroSe conjugan dos elementos en el uso del dinero
Los que en forma conjunta dan origen al
denominado stock final o monto final de la
transacción
Los que en forma conjunta dan origen al
denominado stock final o monto final de la
transacción
Para que exista interés, la
condición es el Tiempo.
Para que exista interés, la
condición es el Tiempo.

8. El Valor del dinero en el tiempo: El
Interes
Gráfico 1
Principal
Interés
Principal
Monto Apertura
Horizonte
temporal
Monto de cierre

9. El Valor del dinero en el tiempo:
El Interés
 En consecuencia el
interés generado por un
principal que se
simboliza con la letra I
esta en función de
múltiples variables, por
ejemplo:
a. La magnitud del principal
colocado o invertido.
b. La tasa de interés
c. El Horizonte temporal, a
mayor tiempo, mayor interés
para un mismo principal y una
misma tasa de interés
d. El riesgo de la operación. A
mayor riesgo mayor tasa de
interés
e. Otras variables económicas,
políticas, sociales, etc.

10. En consecuencia definida I y si designamos
«p» al principal (capital), la tasa de interés es
«j» y «n» el tiempo, el interés se puede
calcular:
I = p.j.n

11. El Valor del dinero en el tiempo:
El Monto (S)
 El Monto de una
cuenta esta
conformado por el
principal más los
intereses devengados
que se generaron a
partir de una tasa de
interés acordada
entre el deudor y el
acreedor.

12. EL MONTO (S)
 Si se conoce el
principal y el interés
generado hasta
determinado momento,
el monto para ese
tiempo se puede
calcular con la
siguiente fórmula:
S = P + I
 Por tanto el interés
acumulado para
determinado horizonte
temporal es el
siguiente:
I = (S/P) – 1

13. Matemática Financiera
Capitalización del Interés
 Si la capitalización se da por única vez
hablamos de interés simple y si concurren
múltiples capitalizaciones
Interés simple
Una capitalización
Interés
Varias capitalizaciones
Interés Compuesto

14. Plazo entre dos fechas : Método
días terminales
 El computo del plazo entre una fecha
inicial y una final, cuando se aplica el
método de días terminales consiste en
considerar todos los días posteriores a la
fecha inicial que no sean posteriores a la
final.
28/05 29/05
28/05 29/05 30/05 01/06 02/06
1 día

15. Plazo entre dos fechas : Método
días terminales
 Ejemplos para depósitos y retiros de ahorro
a) Deposito del 03 de abril retirando el 26 del
mismo mes
b) Depósito del 26 de mayo retirado el 07 de
junio
c) Cuantos días se han acumulado entre el 27
de junio y el 04 de agosto del mismo año

16. Periodo de tiempo bancario
 Los plazos manejados por los bancos son los
siguientes:
Año 360 días
Semestre 180 días
Cuatrimestre 120 días
Trimestre 90 días
Bimestre 60 días
Mes 30 días
Quincena 15 días
Día 1 día

17. Por tanto:
 Una cuenta está bajo un
régimen de interés simple
cuando:
Se produce una sola
capitalización de interés, la
misma que se realiza al
termino del horizonte
temporal pactado, aun
cuando este plazo sea
diferente del plazo de la tasa
de interés simple o tasa de
interés nominal anunciada.
 Por ejemplo, esta tasa
puede ser mensual y el
horizonte de la cuenta
puede ser semestral.

18. Horizonte y sub-horizonte temporal
 El horizonte temporal de una cuenta es el
intervalo de tiempo que existe desde que se
abre la cuenta hasta que se cierra; su plazo se
simboliza con la letra H.
H
momento de apertura momento de cierre

19. Sub-horizonte temporal
 Es un intervalo de tiempo dentro del horizonte
temporal de la cuenta.
 Cuando el horizonte temporal se divide en
sub-horizontes temporales uniformes, su
plazo se simboliza con la letra h; si los sub-
horizontes temporales no son necesariamente
uniformes se simboliza hk.

20. Tasa nominal
 Tasa nominal Siglas
 Anual TNA
 Semestral TNS
 Cuatrimestre TNC
 Trimestral TNT
 Bimestral TNB
 Mensual TNM
 Quincenal TNQ
Diaria TND

21. INTERÉS
SIMPLE
P constante y
j constante
P constante y
J variable
P variable y
J constante
P variable y
J variable
Ecuaciones de
valor
equivalente
Acumulación Amortización
Depósitos
vencidos
Depósitos
acumulados
Cuotas
vencidas
Cuotas
anticipadas
Monto
Renta
uniforme

22. INTERÉS CON PRINCIPAL Y
TASA NOMINAL CONSTANTE
 El principal permanece invariable antes del
cierre de la cuenta.
 La tasa de interés nominal(j) anunciada que se
aplica sobre el principal no sufre variaciones.
 “n” es el número de periodos de la tasa (j) en
el horizonte temporal de la operación; por
ejemplo, si j es mensual, n es el número de
meses en que se divide ese horizonte; si j es

23.  Es anual, n es el número de años en que se
divide ese horizonte temporal, y así
sucesivamente.

24.  Dado que la tasa de interés nominal puede
referirse a diferentes plazos; pueden
presentarse de la siguiente manera:

25. Fórmulas de interés simple

Fórmulas para el cálculo de interés, principal,
tasa de interés nominal constante y número de
periodos de la tasa de interés nominal en una
cuenta de interés simple.
I = Pjn
P =
jn
I
Pj
I
n =
Pn
I
j =

26. Definición de tasa nominal
 Una tasa es un coeficiente que refleja la
relación entre dos magnitudes. Permite
expresar distintas cuestiones, como el interés
(la utilidad, al valor o la ganancia de algo). La
tasa de interés, en este sentido, es un índice
que se expresa en porcentajes y se usa para
estimar el costo de un crédito o la rentabilidad
de los ahorros.

27.  Se conoce como tasa de
interés nominal o tasa
nominal al interés que
se capitaliza más de una
vez al año. Se trata de un
valor de referencia
utilizado en las
operaciones financieras
y es fijado por las
autoridades para regular
los préstamos y
depósitos.
 La tasa nominal es
igual a la tasa de
interés por periodo
multiplicada por el
número de periodos. La
tasa efectiva, en
cambio, es el interés
que paga una persona
por un crédito o cobra
por un depósito.

28. Ejercicios de aplicación
 Ejemplo 1: Si en un banco se coloca un principal de S/1000, a
una tasa j anual de 18%, durante un trimestre, ¿ qué valor toma
n?
 Ejemplo 2: Si se coloca un principal de S/1000, a una tasa de
interés nominal de 1,5 % mensual durante un trimestre, bajo un
régimen de interés simple, ¿ que valor debe tomar n?
 Ejemplo 3: Un banco otorgo a una empresa un préstamo de 10
000 um para ser devuelto dentro de un año, y cobra una TNA
de 24%, ¿ Cuál será el interés simple que pagara la empresa al
vencimiento del plazo?

29.  Ejemplo 4: Una persona deposito 10 000 um en una institución
financiera; este importe genera una TNM de 2%. ¿ qué interés
simple habrá generado ese principal en tres meses?
 Ejemplo 5: ¿Cuál será el interés simple acumulado en 180 días
generado por una cuenta de ahorros abierta con un principal de 1
000 um que devenga una TNA de 24% ?
 Ejemplo 6: El 20 de marzo se abrió una cuenta con 8 000 um en
el Banco del Oriente el mismo que pagaba una TNA de 18%. Se
requiere conocer el interés simple que generó la cuenta hasta el
15 de abril del mismo año. Fecha que se cancelo la operación.
 Ejemplo 7: Calcule el importe con el que se abrio una cuenta,
colocada en un banco a una TNM de 2%, que durante el plazo de
7 meses genero un interés simple de 112 um.

30.  Ejemplo 8: ¿ Qué principal colocado entre el 19 de abril y 30
de junio del mismo año, a una TNM de 2%, producirá un
interés simple de 96 um?
 Ejemplo 9: ¿ Qué principal colocado entre el 19 de abril y 30
de junio del mismo año, a una TNM de 2%, producirá un
interés simple de 96 um?
 Ejemplo 10: Calcula la TNT que se aplico a un principal de
4000 um, que durante el plazo comprendido entre el 5 de
marzo y 17 de julio del mismo año produjo un interés simple
de 297.78 um.
 Ejemplo 11: Calcule el plazo al cual estuvo colocado un
principal de 5000 um, que genero una TNM de 2% y rindió
un interés simple de 350 um.