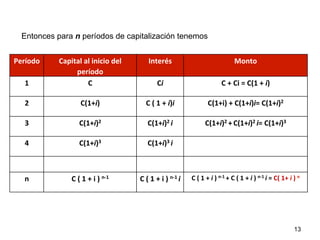
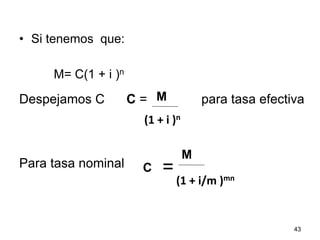
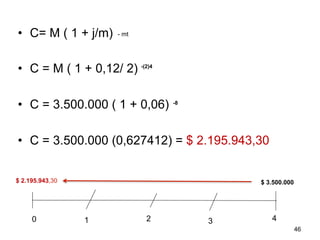
Este documento explica el concepto de interés compuesto, donde los intereses generados se capitalizan periódicamente y generan nuevos intereses. Compara el interés compuesto con el interés simple a través de un ejemplo numérico. Luego presenta la fórmula para calcular el monto a interés compuesto dependiendo de la tasa de interés, el capital inicial y el número de períodos de capitalización.

1. INTERES
COMPUESTO

2. Definición
“El interés compuesto se caracteriza porque el interés generado en un
período de tiempo ,siempre que no se retire, se suma al capital y este
nuevo valor vuelve a ganar intereses y se acumula al nuevo capital. Y
así sucesivamente tanta veces como períodos de capitalización se
hayan establecido. En este método, se dice que los intereses se
capitalizan.”
2

3. COMPARACION CON EL INTERES SIMPLE
Ejemplo
• Calcular el Monto a interés simple y el interés compuesto de un
capital de $ 4.000.000 invertido a una tasa de interés del 10% durante 6
períodos.
a) Interés simple.
I= Cit = 4.000.000 (0,10) (6) = $ 2.400.000
M = C (1+it) = 4.000.000 [1 + 0,10(6)] = $ 6.400.000.-
3

4. b) Interés compuesto
• Para el primer período M= 4.000.000 [1 + 0,10(1)] = $ 4.400.000
• Para el segundo período M = 4.400.000 [1 + 0,10(2)] = $ 4.840.000.
• Para el tercer período M = 4.840.000 [1 +0,10(3)] = $ 5.324.000.
• Para el cuarto período M = 5.324.000 [1 + 0,10(4)] = $ 5.856.400.
• Para el quinto período M = 5.856.400 [1 + 0,10(5)] = $ 6.442.040.
• Para el sexto período M = 6.442.040 [1 + 0,10(6)] = $ 7.086.244.-
4

5. Note la diferencia:
• El Monto final a Interés simple = $ 6.400.000.
• El Monto final a Interés Compuesto = $ 7.086.244.
CONCLUSIONES:
El interés simple es constante durante todo el período
El interés compuesto es creciente a través del tiempo porque los interese
se van capitalizando a través del tiempo
Mientras más períodos se capitalice, mayor será la diferencia entre el IS y
el IC
5

6. VARIABLES DEL INTERES COMPUESTO
• Período de capitalización = n: es el espacio de tiempo en el que el interés
se adiciona o acumula al capital. Este período puede ser anual, semestral,
trimestral, mensual, etc.
• Tasa de interés = i: es la tasa de capitalización del período que puede ser
anual, semestral, trimestral, mensual, diaria, etc.
6

7. Ejemplo:
• Calcular el número de períodos de capitalización y la tasa de interés por
período de capitalización de un capital invertido a interés compuesto
durante 7 años, a una tasa de interés de 15% anual capitalizable
semestralmente.
• t = 7 años
• Entonces:
• n= número total de meses / número de meses del período de capitalización
• n = 7(12)/6 = 14 semestres
7

8. • i= tasa anual/ numero de capitalizaciones al año= tasa anual /m en donde
• m= 360 / Nº de días del período = 360/ 180 = 2
• i = 0,15 anual / 2 (semestres) = 0,075 = 7,5% semestral
8

9. Ejemplo:
• Calcular el número de períodos de capitalización(n) y la tasa de interés por
período de capitalización (i) de un capital colocado a interés compuesto durante
5 años, a una tasa de interés anual del 15%, capitalizable trimestralmente
• t = 5 años
• i= 15%
• n= 5 (12/3) = 20 trimestres
• m= 360 / 90 = 4 significa que se capitaliza 4 veces al año.
• I = 0,15/ 4 (trimestres) = 0,0375 = 3,75% trimestral
9

10. FORMULA DEL MONTO A INTERES
COMPUESTO
• El Monto (M) de un capital invertido a interés compuesto, o monto
compuesto, es el valor del capital final, o capital acumulado, después de
sucesivas adiciones de los intereses.
IC = MC – C
En donde
• IC = interés compuesto
• MC= Monto Compuesto
• C= Capital original
10

11. 11
Ejemplo:
• Calcular el monto (M) a interés compuesto de un capital de $ 100.000 a 4
años plazo invertidos a una tasa del 12% anual.
• Si tenemos que I = Cit
• Primer año:
• I = 100.000(0,12) (1) = $ 12.000.
• M= 100.000 + 12.000 = $ 112.000.
• Segundo año:
• I = 112.000(0,12) (1)= $ 13.440
• M= 112.000 + 13.440= $ 125.440

12. 12
• Tercer año:
• I = 125.440(0,12) (1)= $ 15.052,80
• M = 125.440 + 15.052,80 = $ 140.492,80
• Cuarto año:
• I = 140.492,80(0,12) (1)= $ 16.859,14
• M= 140.492,80 + 16.859,14 = $ 157.351,94
Entonces,
• C= Capital
• i = Tasa de interés por período de capitalización
• n= número de períodos de capitalización

13. Entonces para n períodos de capitalización tenemos
13
Período
Capital
al
inicio
del
período
Interés
Monto
1
C
Ci
C
+
Ci
=
C(1
+
i)
2
C(1+i)
C
(
1
+
i)i
C(1+i)
+
C(1+i)i=
C(1+i)2
3
C(1+i)2
C(1+i)2
i
C(1+i)2
+
C(1+i)2
i=
C(1+i)3
4
C(1+i)3
C(1+i)3
i
n
C
(
1
+
i
)
n-­‐1
C
(
1
+
i
)
n-­‐1
i
C
(
1
+
i
)
n-­‐1
+
C
(
1
+
i
)
n-­‐1
i
=
C(
1+
i
)
n

14. Entonces, para cualquier período de capitalización y tasa de interés por
período, se obtiene la fórmula del monto a interés compuesto:
M= C (1 + i)n
La fórmula del Monto también puede expresarse tomando en cuenta los
períodos de capitalización menor de un año: semestral, trimestral, mensual,
diaria.
14

15. Entonces, el INTERES será
I = M-C
15

16. Fórmula del Monto a interés compuesto en función de m y t
M = C (1 + i/m) mn
En donde:
• M = Monto
• C = Capital inicial
• i = Tasa de interés nominal que puede ser capitalizable varias veces en un
año
• m = número de capitalizaciones al año
• n = número de años
16

17. • Si la capitalización es anual, la fórmula del monto en un año es:
M = C (1+i)n
• Si la capitalización es semestral
M = C (1 + i/2)2
• Si la capitalización es trimestral
M = C (1 + i/4)4
17

18. • Si la capitalización es bimestral
M = C (1 + i/6)6
• Si la capitalización es mensual
M = C (1 + i/12)12
• Si la capitalización es quincenal
M = C (1 + i/24)24
• Si la capitalización es diaria
M = C (1 + i/360)360
18

19. Ejemplo
• Calcular el monto de un capital de $ 200.000 invertido al 12% interés anual
compuesto durante 5 años capitalizable en la siguiente manera:
• Anualmente ( o tasa efectiva)
M= 200.000(1+0,12)5 = $ 352.468,34
• Capitalizable semestralmente
M = 200.000(1+0,12/2)10 = $ 358.169,54
• Capitalizable trimestralmente
M = 200.000(1+0,12/4)20 = $ 361.222,25
19

20. • Capitalizable bimestralmente
M = 200.000(1+0,12/6)30 = $ 362.272,32
• Capitalizable mensualmente
M = 200.000(1+0,12/12)60 = $ 363.339,34
• Capitalizable diariamente
M = 200.000(1+0,12/360)1.800 = $ 364.387,33
OBSERVE QUE CUANDO EL PERIODO DE CAPITALIZACION AUMENTA,
AUMENTA EL MONTO PORQUE AUMENTA EL INTERES COMPUESTO
20

21. Ejemplo:
• Una empresa obtiene un préstamo de $ 3.000.000 a 6 años plazo a una
tasa de interés anual del 15% capitalizable semestralmente. Calcular el
monto que debe pagar al vencimiento y el interés pagado.
• M= 3.000.000(1+0,15/2)12 = 3.000.000(1,075)12
• = 3.000.000(2,381780)= $ 7.145.338,80
• Interés que debe pagar:
• I = M – C
• I = 7.145.338,80 – 3.000.000 = $ 4.145.338,80
21

22. Monto Compuesto con períodos de capitalización
fraccionarios
Cuando el tiempo de pago no coincide con el período de capitalización, se
presenta este caso
Ejemplo:
Calcular el valor de una deuda de $ 4.000.000 contraída a interés
compuesto durante 6 años y 3 meses plazo, a una tasa de interés anual del
14% capitalizable semestralmente.
22

23. • Resolucion
Toma el valor exacto de n en la fórmula del Monto compuesto
Entonces tenemos:
• n = 6(12) + 3 / 6 = 75/6 = 12, 5 semestres
• i = 0, 14/2= 0, 07 semestral (7% semestral)
• M = 4.000.000 (1 +0, 07)12.5 = 4.000.000(2, 329685)= $ 9.318.740,34
23

24. Ejemplo:
• Calcular el Monto compuesto de un capital de $ 2.000.000 invertido a 7
años y 8 meses plazo a una tasa anual del 18% capitalizable
trimestralmente
Calculo n e i
• n= 7(12)+8/ 3 = 84+8 /3 = 30,6667 trimestres
• i = 0,18/4 = 0,045 trimestral
M= 2.000.000(1+0,045)30,6667= $ 7.713.714,13
24

25. EJERCICIOS
1.- Una empresa obtiene un préstamo de $ 4.000.000. a 10
anos plazo a una tasa de interes del 15% anual
capitalizable semestralemente . Calcule el interés y el
Monto que debe pagar en la fecha de vencimiento.
2.- Una persona toma un depósito a plazo en su libreta de
ahorros de $ 3.000.000. al 12% de interés anual
capitalizable trimestralmente. Cuanto habrá en su libreta
ala cabo de 8 años y 6 meses.
25

26. 3.- Calcule el Monto a interes compuesto de un Capital de $
1.000.000 invertido al 12% anual durante 10 años.
4.- Rubén abre una cuenta de ahorros hoy, con $ 800.000.
a una tasa de interés del 14% capitalizable
semestralmente .Calcule cuanto habrá en la cuenta al
cabo de 7 años y 7 meses.
26

27. CALCULO DE LA TASA DE INTERES
LA TASA NOMINAL O EFECTIVA DE INTERES
SE PUEDE CALCULAR PARTIENDO DE LA
FORMULA DEL MONTO
M = C ( 1 + i ) n ; M= C ( 1 + i/m)mn
Y DESPEJAMOS APLICANDO LOGARITMOS
27

28. M
C
M
C
28
log (1 + i )
n
n log (1 + i )
M
C
n
log (1 + i )
log
log
log

29. O TAMBIEN
i =
29
M
C
1/ n
- 1

30. EJEMPLO
A qué tasa efectiva se convertirá un capital
de $ 300.000 en un monto de
$ 450.000 al cabo de 6 anos?
M = C ( 1 + i ) n
M/C = ( 1 + i )n
30

31. 450.000 / 300.000 =( 1 + i ) 6
1,5 = ( 1 + i ) 6
Aplicamos logaritmos
log1,5 = log( 1 + i ) 6
log1,5 = 6 log( 1 + i )
log1,5 /6 = log( 1 + i )
0,029348= log( 1 + i )
antilog 0,029348= 1 + i
31

32. 1, 069913 = 1 + i
0,069913 = i
i = 6,99132 %
32

33. ACTIVIDADES DE EJERCITACION
• A q u é t a s a a n u a l c a p i t a l i z a b l e
trimestralmente, un capital de $ 400.000
se convertirá en ¾ veces más al cabo de
5 años?
• A qué tasa efectiva es equivalente la tasa
del 11,35037% anual capitalizable
trimestralmente?
33

34. • A qué tasa efectiva se convertirá un capital de $
500.000 en un Monto de $ 900.000 en 9 anos y
6 meses?
• A que tasa de interés annual capitalizable
trimestralmente se debe colocar un capital de $
1.000.000 para que produzca un Monto de $
5.500.000 en 6 anos y 9 meses.A qué tasa
efectiva equivale?
34

35. CALCULO DEL TIEMPO
A INTERES COMPUESTO
PARA CALCULAR EL TIEMPO, SE DEBE
CALCULAR PRIMERO n, POR LO CUAL SE
APLICA LA FORMULA DEL MONTO
M = C ( 1 + i ) n ; M= C ( 1 + i/m)mn
M = C ( 1 + i ) n
35

36. 36
M
C
M
C
log (1 + i )
n log (1 + i )
n
log
log
log
M
C
log (1 + i )
n

37. EJEMPLO
En qué tiempo un capital de $ 1.000.000. se
convertirá en $ 1.500.000. a una tasa de interés
efectiva del 18%?
Tenemos:
• M = $ 1.500.000
• C = $ 1.000.000
• i = 18%
37

38. • M/C = ( 1 + i )n
• 1.500.000 / 1.000.000 = ( 1 + 0,18)n
• 1,5 = ( 1 + 0,18)n
• log 1,5 = log ( 1 + 0,18 )n
• log 1,5 =n log ( 1 + 0,18)
• n=log 1,5 / log (1+0,18)
• n = 0,176091/0,071882
• n= 2,449726 anos (1 ano = 360 días, 0,449726 son x
días)
• n= 2 anos, 5 meses, 12 días
38

39. EJERCICIOS
• En qué tiempo un capital de $ 700.000 se
duplicará invertido a una tasa del 18%
capitalizable semestralmente?
• En qué tiempo un capital de $ 2.500.000 , se
convertirá en $ 5.625.000 invertido a una tasa
de interés anual del 24% capitalizable
semestralmente?
39

40. • En cuantos anos aumentará en ¾ su valor un
capital de $ 600.000 invertido a una tasa de
interés del 17% capitalizable semestralmente ?
40

41. VALOR ACTUAL A INTERES
COMPUESTO
• El VAC es el valor de un documento, inversión o
deuda, antes de la fecha de su vencimiento,
considerando determinada tasa de interés
• VAC significa el valor de un pago futuro en una
determinada fecha antes de su vencimiento
41

42. Responde por ejemplo a :
• Cuanto vale HOY día una deuda de $ 1.000.000
que vencerá en 5 anos mas ?
• En cuanto se puede vender HOY un documento
de $ 5.000.000 que en vence en 4 anos más?
42

43. • Si tenemos que:
M= C(1 + i )n
Despejamos C C = para tasa efectiva
Para tasa nominal =
43
M
(1
+
i
)n
C
M
(1
+
i/m
)mn

44. • Para el cálculo del VAC (entre la fecha de
suscripción y la fecha de vencimiento) pueden
haber dos casos generales:
• Caso 1: Cuando conocemos el valor que tendrá
un documento al cabo de n periodos ( o sea,
conocemos el Monto)
• Caso 2 : Cuando conocemos el valor hoy día del
documento que gana interés. En este caso
desconocemos el Monto (hay que calcularlo).
44

45. Ejemplo Caso 1:
• Cual es el VAC de un pagaré cuyo valor al
vencimiento al final de 4 años es $ 3.500.000,
considerando una tasa de interés del 12% anual
capitalizable semestralmente?
Entonces tenemos que :
• M=$ 3.500.000.-
• J = 0,12
• m = 2
• t = 4
45

46. • C= M ( 1 + j/m)
• C = M ( 1 + 0,12/ 2)
• C = 3.500.000 ( 1 + 0,06)
• C = 3.500.000 (0,627412) = $ 2.195.943,30
46
- mt
-(2)4
-8
10 2 3 4
$ 2.195.943,30 $ 3.500.000

47. 47
Ejemplo Caso 2:
• Cual es el VAC de un pagaré cuyo valor nominal
es $ 500.000 a 6 años plazo considerando una
tasa de interés del 12% anual capitalizable
semestralmente desde su suscripción si se
vende dos años antes de la fecha de
vencimiento , considerando una tasa anual del
14% capitalizable semestralmente?

48. Solución gráfica
48
0 1 2 3 4 5 6
$ 500.000 M= ?C= ?

49. Entonces primero se calcula el Monto a 6 anos:
• M = C ( 1 + i/m)
• M = 500.000 ( 1 + 0,12/ 2)
• M = 500.000 ( 2,012196)
• M = $ 1.006.098,236
49
mn
2(6)

50. Ahora calculamos el VAC 2 anos antes de su
vencimiento
C = M (1 + i/m)
C = 1.006.098,236 ( 1 + 0,14/ 2)
C = 1.006.098,236 (0,762895)
C = $ 767.547,58 ( VAC)
50
-mn
-2(2)

51. VAC CON TIEMPO FRACCIONARIO
Para calcular el VAC con períodos de
capitalización fraccionarios, utilizamos la fórmula
del interés compuesto
C = o lo que es lo mismo
C = M ( 1 + i )
51
M
(1 + i )
n
-n

52. Ejemplo
El valor de un pagaré al cabo de 7 anos será
$3.400.000.
Calcular su VAC luego de transcurridos 3 años y
4 meses de la fecha de suscripción ,
considerando una tasa de interés del 14%
capitalizable semestralmente
M = $ 3.400.000
i/2 = 0,14 /2 = 0,07
52

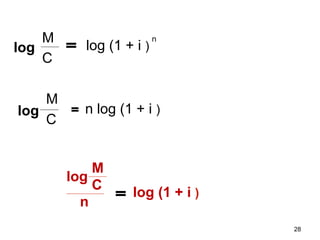
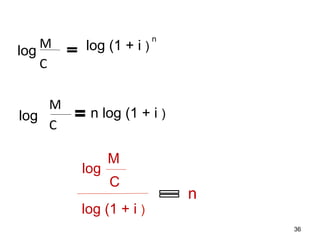
53. Calculamos primero el tiempo
n
Aplicamos la fórmula:
C
C = $ 2.070.131,25
53
=
(7)(12) – [ (3)(12) + 4 ]
6
= 44/ 6 = 7,3333
= $ 3.400.000( 1 + 0,14/2)
- 7,3333

54. EJEMPLO
Luego de 3 años y 3 meses de la fecha de
suscripción se negocia un documento suscrito el
día de hoy por $ 2.800.000 a 6 años 9 meses
con una tasa de interés del 12% capitalizable
semestralmente. Calcular el valor actual a dicha
fecha considerando una tasa de interés del
11,25% efectiva.
54

55. • Se calcula el Monto al final de los 6 años y 9
meses
n
M 2.800.000 ( 1 + 0,12/2)
M $ 6.148.755,355
55
=
(6)(12)+ 9
6
=
81
6
= 13 3/6 = 13,5
=
13,5
=

56. Ahora se calcula el valor actual a los 3 años y 3
meses, si la tasa de interés es del 11,25%
efectiva
El tiempo que falta para el vencimiento del
documento es:
n
C = $ 6.145.755,355 (1+0,1125)
C = $ 4.233.866,90
56
=
[6(12) +9] – [3(12)+3]
6
= 3,5 anos
- 3,5

57. EJERCICIOS
• Calcule el VAC de un pagaré cuyo valor al
término de 3 años y 6 meses será de $
2.100.000 considerando una tasa de interés del
16% anual capitalizable semestralmente.
• Un documento suscrito hoy por $ 950.000 a 5
años plazo a una tasa del 17% anual
capitalizable semestralmente , se vende dos
anos antes de la fecha de su vencimiento
considerando una tasa del 18% anual
capitalizable semestralmente. Calcule el VAC a
esa fecha
57