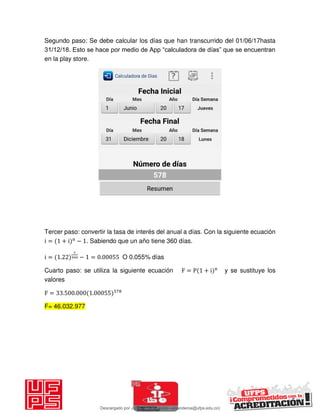
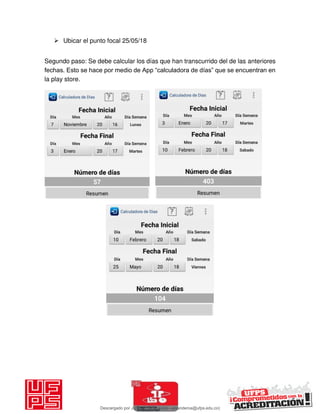
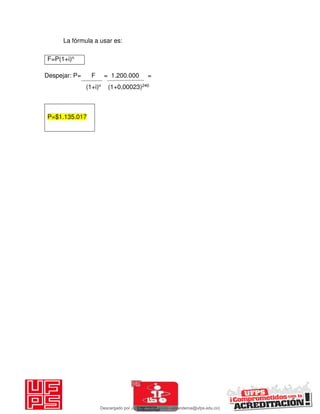
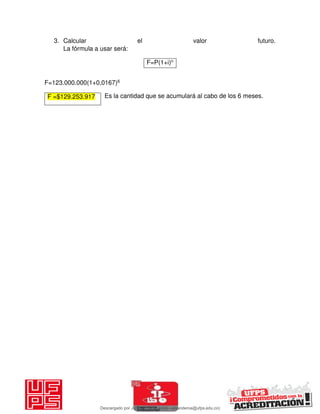
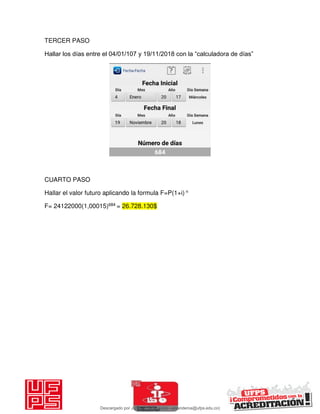
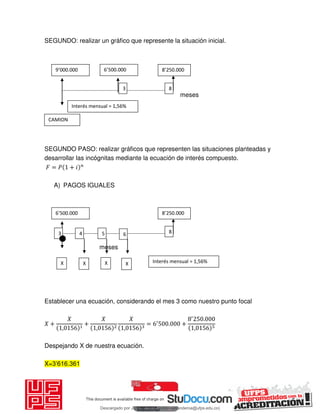
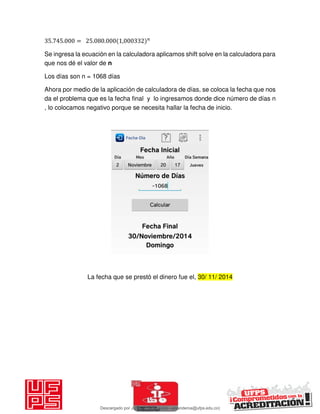
El documento presenta 125 ejercicios resueltos sobre interés compuesto en ingeniería económica, destinado a estudiantes de la Universidad Francisco de Paula Santander. Se busca complementar el aprendizaje teórico con práctica para facilitar la toma de decisiones financieras. Incluye distintos problemas con soluciones completas y fórmulas relacionadas a la matemática financiera.