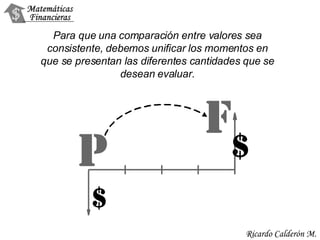
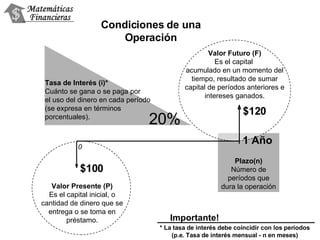
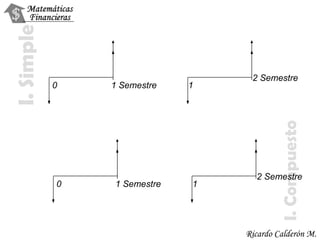
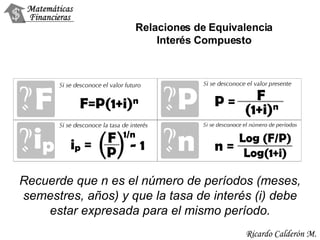
Este documento trata sobre el valor del dinero en el tiempo y las matemáticas financieras. Explica conceptos como tasas de interés, valores presentes, valores futuros, rentabilidad e interés simple vs. interés compuesto. Incluye ejemplos y ejercicios para practicar estos conceptos.

1. Ricardo Calderón M. Febrero 2007

2. Este material está incompleto! Le invito a que complete lo que falta, lo que falta es su interés por el tema, un poco de dedicación y sus valiosos aportes que surgen de la curiosidad, experiencia e interacción con otras personas. Recuerde lo que dijó Lao Tse (430 A.C). “ Si tu me hablas, yo escucharé, si me muestras, podré ver, pero si me dejas tomar parte, aprenderé.”

3. Alguna vez se ha preguntado por qué razón... Hace unos meses le ofrecían otras tasas de interés Un crédito que parecía tener unas condiciones pactadas luego cambia. En el banco vecino pagan tasas superiores Si le presta a un amigo su dinero puede ganar más que prestándolo a un banco. Unos bancos ofrecen regalos y otros no

4. El concepto fundamental de las matemáticas financieras es el valor del dinero en el tiempo. El dinero tiene un valor dependiendo del momento en que se considera, por lo cual toda cantidad de dinero se debe identificar por una magnitud y una ubicación en el tiempo ... ... se debe distinguir ¿ Cu á ndo ? y ¿ Cu á nto ?

5. Contenido Valor del Dinero con el Tiempo ¿Cómo comparamos sumas de dinero ubicadas en diferentes momentos del tiempo? ¿Cuánto ganamos porcentualmente en una operación? ¿De qué forma se puede devolver el capital que ha sido prestado y pagar los intereses correspondientes? ¿Cómo se deben trabajar tasas como DTF, Inflación, Devaluación, Libor y Prime? Tasas de Interés ¿Qué son tasas de interés nominales, efectivas o periódicas? ¿Cómo convertirlas? Amortización de Créditos

6. Valor del dinero en el tiempo

7. Objetivos de este capítulo Entender e interpretar el significado del valor del dinero en el tiempo. Aplicar las relaciones de equivalencia para hallar tasas de interés, valores presentes y valores futuros. Calcular rentabilidades y comparar tasas de interés para diferentes modalidades de inversión y de crédito.

8. Por interés entiendo... Tasa de interés para mi es ...

9. Valores ubicados en distintos momentos en el tiempo no son comparables. Sin embargo, es posible "mover" las cantidades de un momento del tiempo a otro, hallando valores que sean equivalentes. ¿Qué es una equivalencia?

10. El interés se establece por un período de tiempo determinado. Suponga que... Existen un local por el cual se paga un canon de arrendamiento de $200 mensuales ... Si arrendamos el local por un mes pagaremos ... Si arrendamos el local por un año pagaremos ... ¿Qué opción sale más costosa? Entonces, ¿Cómo debemos medir el costo de una operación financiera?

11. Factores determinantes del costo del dinero

12. Para que una comparación entre valores sea consistente, debemos unificar los momentos en que se presentan las diferentes cantidades que se desean evaluar.

13. Condiciones de una Operación 0 $100 20% Valor Presente (P) Es el capital inicial, o cantidad de dinero que se entrega o se toma en préstamo. Plazo(n) Número de períodos que dura la operación Tasa de Interés (i)* Cuánto se gana o se paga por el uso del dinero en cada período (se expresa en términos porcentuales). * La tasa de interés debe coincidir con los períodos (p.e. Tasa de interés mensual - n en meses) Importante! 1 Año $120 Valor Futuro (F) Es el capital a cumulado en un momento del tiempo, resultado de sumar capital de períodos anteriores e intereses ganados.

14. Suponga una inversión ... Un ahorrador deposita su dinero en el Banco (Abre un Certificado de Depósito a Término – CDT) por $100 millones El Banco promete pagarle un 4% de intereses por cada semestre. ¿Cuánto tiene acumulado el ahorrador al cabo de un año? Ejercicio de Orientación

15. ¿Pueden los intereses volverse parte del capital y ganar más intereses en períodos futuros?

16. 0 1 Semestre 1 2 Semestre 0 1 Semestre 1 2 Semestre

18. Las diferencias entre interés simple e interés compuesto son ...

19. Relaciones de Equivalencia Interés Compuesto Recuerde que n es el número de períodos (meses, semestres, años) y que la tasa de interés (i) debe estar expresada para el mismo período.

20. Importante! Una operación financiera no es sólo cuestión de números! Las decisiones de inversión y financiación se toman con base en ... Algunos cálculos matemáticos Expectativas

21. Si usted invierte $10 millones y le ofrecen una tasa mensual del 2% constante durante el tiempo que mantenga la inversión, ¿cuánto dinero recibiría al cabo de 1 año? ¿Cuánto dinero recibiría al cabo de 5 años? ¿Cuánto dinero recibiría al cabo de 10 años? Ejercicios de Valor del Dinero en el Tiempo

22. 2. Un título valor establece que al término de 3 años se recibirá una única suma de dinero $100 millones. Para obtener una rentabilidad mensual del 1% ¿cuánto dinero debe invertirse? Ejercicios de Valor del Dinero en el Tiempo

23. 3. Una inversión de $15 millones produce luego de tres meses $15’500.000. ¿Qué rentabilidad se obtiene? En términos mensuales En términos trimestrales En términos anuales Ejercicios de Valor del Dinero en el Tiempo

24. 4. Multitel Ltda obtuvo un sobregiro por $12’215.300 el día 3 de febrero de 2007. Si se pactó para la operación un costo equivalente a la tasa máxima legal vigente, ¿Qué saldo quedó en la cuenta corriente luego de consignar $14 millones el día 21 de febrero? Ejercicios de Valor del Dinero en el Tiempo

25. 5. Para unos excedentes que tiene una empresa ($100 millones), el tesorero ha encontrado dos alternativas de inversión aceptables que son: Depositar el dinero en un CDT ($100 millones) y obtener $101,5 millones al cabo de 92 días. Comprar un título valor por el cual debe pagar $99’115.000 y recibirá 65 días después $100 millones. ¿Qué alternativa resulta más rentable? ¿Qué debería hacer el tesorero? Ejercicios de Valor del Dinero en el Tiempo

26. 6. Un ahorrador planea realizar depósitos mensuales para acumular un capital con el fin de iniciar una empresa (la tasa de interés ofrecida es 1% mensual). Al inicio del año deposita $500.000, un mes después no logra realizar ningún depósito, por lo cual al mes siguiente hace un esfuerzo y deposita $900.000. Al finalizar el siguiente mes de nuevo deposita $500.000 y decide averiguar el saldo. ¿Cuánto tiene acumulado? Ejercicios de Valor del Dinero en el Tiempo