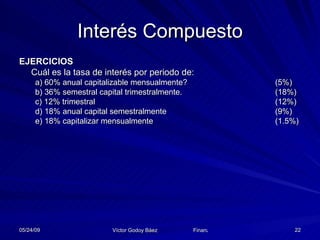
El documento presenta el calendario de evaluaciones para una clase que comienza el 11 de agosto de 2008 y termina el 22 de diciembre de 2008. Habrá tres evaluaciones sumativas y cuatro controles a lo largo del semestre. Las evaluaciones sumativas representarán el 25%, 25% y 30% de la nota respectivamente.

1. Calendario de Pruebas, Controles Son 20 clases, las que se inician el día 11/08/2008 y la última será el 22/12/2008 (Examen). Realizaremos tres(3) evaluaciones sumativas, la primera el 15/09/2008(I-II Unidad), la segunda el 27/10/2008(III Unidad), y la tercera el 02/12/2008 (IV y V Unidad). (25%; 25% y 30% respectivamente) y cuatro controles: 19/08/2008 (5%); 02/09/2008 (5%); 07/10/2008 (5%); 11/11/2008 (5%)

2. FINANZAS 88 HORAS PRIMAVERA 2008 VICTOR GODOY BAEZ INGENIERO COMERCIAL - MBA [email_address]

3. Contenidos Programáticos Consideraciones Generales 14 Horas Bases de Administración Financiera 12 Horas Análisis y Planeación financiera 30 Horas Elementos de Gestión en Administración Financiera 12 Horas Administración Financiera de corto Plazo 14 Horas Evaluaciones 06 Horas

4. I UNIDAD Consideraciones Generales Reconocer Conceptos Básicos del ámbito financiero Reconocer diferentes características de los conceptos y materias financieras

5. Diagnóstico Ejercicios Encontrar 4% de 725 (29) 175% de 800 (1.400) 2½% de 35.640 (891,02) ¾% de12.000 (90.000) ¿Qué % de: 40 es 20 (50%) 31 es 620 (2.000%) ¿De qué número. Es 20 el 25%? (80) Sobre una inversión de US $2.500, M obtiene una utilidad de $131,25 ¿Qué % de la inversión representa dicha utilidad? (5 ¼%) Un abogado recupera el 90% de una demanda de US$300 y cobra por concepto de servicios el 15% de la suma recuperada ¿Qué cantidad recibirá su cliente? (229,50)

6. El Valor del Dinero en el Tiempo El dinero es un activo que cuesta conforme transcurre el tiempo. Ejemplo: De las siguientes opciones ¿Cuál elegiría? Tener M$1.000 hoy u Obtener M$1.000 dentro de un año. Ambas 100% seguras

7. El Valor del Dinero en el Tiempo Indudablemente, cualquier persona sensata elegiría la primera, M$1.000 valen más hoy que dentro de un año. Ahora si se tratara de: Tener M$1.000 hoy u Obtener M$1.500 dentro de un año Ambas 100% seguras

8. El Valor del Dinero en el Tiempo La elección es más difícil, la mayoría elegiría la segunda. Contiene un “premio por esperar” llamada TASA DE INTERES, del 50%. Generalmente en el mercado, esta tasa de interés lo determina el libre juego de la oferta y demanda. “No sumas ni restas”

9. El Valor del Dinero en el Tiempo Suponga que Ud. que dispone de M$1.000 y le ofrecen un interés de 10% anual en los próximos 3 años. Ud. recibe y retira el interés a fin de año Ud. recibirá y retirará el dinero y los intereses a fin del año 3.

10. El Interés Es la cantidad pagada por el uso del dinero obtenido en préstamo o la cantidad producida por la inversión del capital La Tasa de interés: Es la razón del interés al capital, en la unidad de tiempo.

11. El Interés Designamos por C a una cierta cantidad de dinero en una fecha dada cuyo valor aumenta a S en una fecha posterior C se conoce como capital, S se conoce como monto o valor acumulado de C I=S – C se conoce como interés

12. El Interés Ejemplo: B obtiene de L un préstamo de $500.000 y al final del año le paga $525.000. En este caso C = $500.000, S = $525.000 e I= S – C = $25.000 I 25 i=------ = ------- = 0,05 P 500

13. Interés Simple Cuando únicamente el capital gana intereses por todo el tiempo que dura la transacción, al interés vencido al final del plazo se le conoce como: Interés simple. El interés simple sobre el capital C, por t años a la tasa i, está dado por la expresión: I = Cit

14. Interés Simple Y el monto simple está dado por: S = C + I = C + Cit = C(1+ it) Determinar el interés simple sobre $750.000 al 4% durante ½ año ¿Cuál será el monto? En este caso C=750.000, i=0,04 y t= ½, por lo cual I = Cit = 750.000(0,04) ½ = $15.000 S= C + I = 750.000 + 15 = 765.000

15. Interés Simple Ejercicios Encontrar el interés simple y el monto de $1.000 Al 4½% , durante un 1 año (I:$45; S:$1.045) Al 5¼%, durante 2 años. (I:$105; S:$1.105) Al 3½%, durante ½ año (I:$17,50; S:$1.017,50) Al 6%, durante 8 meses (I:$40; S:$1.040) Al 4%, durante 15 meses (I:$50; S:$1.050) Al 5%, durante 10 meses (I:$41,67; S:$1.041,67)

16. Interés Simple Valor Presente de una deuda Es el valor de una deuda en una fecha anterior a la de su vencimiento. El valor presente a la tasa interés simple i, del monto S, con vencimiento en t años es: S C = -------- 1 + it

17. Interés Simple Ejemplo: Encontrar el valor presente, al 6% de interés simple, de $1.500 con vencimiento en 9 meses. En este caso, S = 1.500; i=0,06; t=9/12 Luego, 1.500=[1+(0,06)(9/12)] = C(1,045) C=1.500/1,045=$1.435,41 es el valor presente

18. Interés Simple Ejercicios ¿Qué suma debe ser invertida al 5% para tener $1.000 después de 8 meses? ($967,74) ¿Qué capital produce en 8 meses, $48 al 6% ($1.200) b) $50 al 5% ($1.500) ¿En qué tiempo un capital de $3.000, Produce $90 al 4% de interés simple (9 meses) Alcanza un monto de $3.100 al 5% de interés simple (8 meses)

19. Interés Simple Determinar el valor de un préstamo de $2.500 con vencimiento dentro de 9 meses, suponiendo un rendimiento de 6% El día de hoy ($2.392,34) Dentro de 3 meses ($2.427,18) Dentro de 7 meses ($2.475,25) Dentro de 1 año ($2.537,50)

20. Interés Compuesto En el interés compuesto los intereses que se van generando se van incrementando al capital original en periodos establecidos y a su vez van a generar un nuevo interés adicional para el siguiente lapso. El interés se capitaliza. Periodo de capitalización .- El interés puede ser convertido en Anual, semestral, trimestral y mensualmente.

21. Interés Compuesto Frecuencia de Conversión .- Número de veces que el interés se capitaliza durante un año (n). El periodo de tiempo entre dos conversiones sucesivas se conoce como periodo de conversión o periodo de interés. Tasa de Interés compuesto. - Se expresa comúnmente en forma anual indicando si es necesario su periodo de capitalización. Ej. 8% anual capitalizable mensualmente.

22. Interés Compuesto EJERCICIOS Cuál es la tasa de interés por periodo de: a) 60% anual capitalizable mensualmente? (5%) b) 36% semestral capital trimestralmente. (18%) c) 12% trimestral (12%) d) 18% anual capital semestralmente (9%) e) 18% capitalizar mensualmente (1.5%)

23. Interés Compuesto Por interés al 6% se entiende que el 6% se convierte anualmente. Conclusiones a) Interés compuesto es mayor que el interés simple. b) A mayor frecuencia de conversión mayor será el interés siendo igual la tasa anual nominal. Ej. un depósito que obtenga intereses mensualmente tendrá mayor rendimiento que uno que los obtenga trimestralmente.

24. Interés Compuesto Ejemplo: Hallar el interés simple sobre $1.000 por 3 años al 5% de interés simple. ($150) Hallar el interés compuesto sobre $1.000 por 3 años si el interés de 5% es convertible anualmente en capital. ($157,62)

25. Interés Compuesto Tasa nominal tasa efectiva y tasa equivalente.- Cuando se utiliza una operación financiera, se pacta una tasa de interés anual que rige durante el lapso que dure la operación. Tasa Nominal de Interés.- Tasa de interés anual que rige durante el lapso que dure la operación. Tasa efectiva anual. - Si el interés se capitaliza en forma trimestral, semestral, mensual, la cantidad efectivamente pagada o ganada es mayor que si se compone en forma anual. Tasas equivalentes. - Dos tasas con diferentes periodos de capitalización serán equivalentes, si al cabo de un año producen el mismo interés compuesto.

26. Interés Compuesto Al final de un año, el monto compuesto de $100 al 4% convertible trimestralmente es 100(1,01)^4= $104,06 4,06% convertible anualmente es 100(1,0406)= $104,06 Por tanto, 4% convertible. trimestralmente y 4,06% convertible anualmente son tasas equivalentes

27. Interés Compuesto En el ejemplo 4% es la tasa nominal y 4,06% es la tasa efectiva

28. Monto Compuesto Sea un capital C invertido a la tasa i por periodo de conversión y designamos con S al monto compuesto de C al final de n periodos de conversión. Puesto que C produce Ci de interés durante el primer periodo de conversión, al final de dicho periodo produce a C + Ci= C(1 + i)

29. Monto Compuesto En otras palabras, el monto de un capital al final de un periodo de conversión se obtiene multiplicando el capital por el factor (1 + i). En consecuencia, al final del segundo periodo de conversión el capital es C(1+i)*(1+i)= C(1+i) ² y asi sucesivamente al final del tercer, cuarto, etc periodo

30. Monto Compuesto La sucesión de montos C(1+i), C(1+i) ², C(1+i)³ ….. Forma una progresión geométrica cuyo n-ésimo término es: S=C(1+i)ⁿ

31. Monto Compuesto El factor (1+i)ⁿ es el monto compuesto de 1 a la tasa i por periodo, por n periodos de conversión y será conocido como el monto compuesto de 1