Matlab sesion3

Universidad Nacional de Ingeniería Universidad Nacional de Ingeniería
Facultad de Ingeniería Eléctrica y Electrónica MATLAB Facultad de Ingeniería Eléctrica y Electrónica MATLAB
Lima – Perú NIVEL BÁSICO Lima – Perú NIVEL BÁSICO

SESIÓN No. 3

Gráficas Gráficas en MATLAB

Gráficas MATLAB
Anatomía de las Gráficas
Gráficas Bidimensionales
Procesos para el trazado de una gráfica
Graficas Tridimensionales
Creación de una gráfica

http://matlabperu.blogspot.com
Herramientas de exploración gráfica
Algunas Herramientas GUI
Gráficos especializados

EXPOSITOR: http://matlabperu.blogspot.com EXPOSITOR: http://matlabperu.blogspot.com
Miguel Ataurima Arellano ataurima@telefonica.net.pe Miguel Ataurima Arellano ataurima@telefonica.net.pe
INGENIERO CONSULTOR
ma2lac@msn.com 1 INGENIERO CONSULTOR
ma2lac@msn.com 2

Anatomía de las gráficas en MATLAB Procesos para el trazado de una gráfica

El entorno MATLAB ofrece una variedad de ejemplo1.m Una gráfica es la traza de datos, los cuales pueden ser generados por código
funciones para la gráfica de datos además MATLAB, por ejemplo a través de una regla de correspondencia aplicada sobre un
x = 0:0.2:20; código
de herramientas GUI para crear y x = 0:0.2:20;
y = sin(x)./sqrt(x+1); fuente dominio; o pueden ser importados de alguna base de datos, como un archivo de
y = sin(x)./sqrt(x+1);
modificar la visualización de las gráficas. y(2,:) = sin(x/2)./sqrt(x+1);
y(2,:) = sin(x/2)./sqrt(x+1);
y(3,:) = sin(x/3)./sqrt(x+1); Excel.
Una figura es una ventana MATLAB que y(3,:) = sin(x/3)./sqrt(x+1);
plot(x,y)
plot(x,y)
contiene la visualización de una gráfica
DATOS
(usualmente trazado de datos) y
componentes UI.
Un trazado (plot) es cualquier visualización
Sea bidimensional o tridimensional, el proceso de trazado de una gráfica esta
gráfica, a partir de un conjunto de datos,
que se pueda crear dentro de una ventana constituido por las siguientes etapas
figura. ƒ Creación de la gráfica
Una gráfica (graph) es el conjunto de uno ƒ Exploración de datos
o mas trazas en ejes bidimensionales o ƒ Edición del gráfico
tridimensionales. ƒ Adición de anotaciones al gráfico
Ventana figura
ƒ Impresión y Exportación de gráficas
(figure)
ƒ Adición y eliminación de contenido de una ventana figure
Eje ƒ Almacenamiento y reutilización de gráficas (*.fig)
(axes)
Cada una de estas etapas se pueden desarrollar a través de código (funciones y/o
Trazas de curvas
scripts) o utilizando las herramientas que provee MATLAB.
(plots)

Copyright © 2008 – ataurima@telefonica.net.pe 3 Copyright © 2008 – ataurima@telefonica.net.pe 4
1

Creación de una gráfica Algunas Herramientas GUI

Preparar los datos a graficar. Barra de herramientas de las Ventana figure
ƒ Los datos deben estar en el workspace. Modo edición Zoom in/out Barra de colores Legenda

Especificar la ventana figura en la que se desea hacer la gráfica.
ƒ Usando el comando figure.
Hace la subdivisión de la gráfica en sub-gráficas (ejes) si es necesario. Pan Rotador Cursor Pincel Data Link Oculta/Muestra herramientas
3D de Datos de Datos de trazado
Especificar la sub-gráfica (eje) en la que se desea hacer la gráfica .
Otras herramientas (menú View)
ƒ Usando el comando subplot.
ƒ Cámara
Efectuar el trazado de la gráfica.

iluminación
Controles de movimiento Selector de ejes Tipo de
ƒ Usando las funciones trazadoras de gráfica bidimensional/tridimensional. de cámara principales Proyección Reset y Stop
Agregar detalles a la gráfica . Jerarquía de
root
ƒ Legenda, enrejado, título, etiquetas, etc. objetos gráficos

Estableciendo valores a las propiedades figure
de los objetos que componen la gráfica. ƒ Edición de trazas
ƒ Creando manipuladores
edición de propiedades de Fija objetos en una posición
a los objetos de la gráfica. Anotaciones objetos gráficos específica
Alinea objetos
objetos UI axes
ocultas de ejes
ƒ Obteniendo/estableciendo
propiedades mediante
los comandos get y set. objetos de Grupo de Anotaciones de
objetos núcleo
trazado objetos objetos


Universidad Nacional de Ingeniería Funciones Gráficas Bidimensionales
Facultad de Ingeniería Eléctrica y Electrónica MATLAB
Lima – Perú NIVEL BÁSICO

Linea

Barra
Gráficas Bidimensionales agrupada apilada agrupada apilada

Área
Funciones trazadoras de Gráficas Bidimensionales.
La función de trazado lineal bidimensional: plot.
Control de ejes y anotaciones. Direccional
Múltiples ejes en una ventana figura.
Ejemplos con funciones para el trazado de líneas, barra, gráficas dispersas,
funciones polares, funciones paramétricas, campos vectoriales y funciones
Radial
animadas.

Dispersas
(Scatter)
EXPOSITOR: http://matlabperu.blogspot.com
Miguel Ataurima Arellano ataurima@telefonica.net.pe
INGENIERO CONSULTOR
ma2lac@msn.com 7 Copyright © 2008 – ataurima@telefonica.net.pe 8
2

La función de trazado bidimensional: plot

Se deben seguir los siguientes pasos: ws La función plot, procede a desarrollar el trazado de la siguiente manera
ƒ Preparar los datos por graficar (coordenadas de x y
los puntos. >> plot(x,y);
ws
x = (0:pi/4:2*pi)'; 0 0
0.7854 0.7071
y = sin(x); 1.5708 1.0000 x y
2.3562 0.7071
3.1416 0.0000
ƒ Con estos vectores se efectúa la gráfica 3.9270 -0.7071
3
4.7124 -1.0000 1 0 0
haciendo uso de las funciones MATLAB para el
5.4978 -0.7071 2
trazado bidimensional 6.2832 -0.0000 2 0.7854 0.7071 4

3 1.5708 1.0000
plot(x,y);
4 2.3562 0.7071 5 9

1
5 3.1416 0.0000

6 3.9270 -0.7071

7 4.7124 -1.0000 6 8

8 5.4978 -0.7071 7

9 6.2832 -0.0000


EJEMPLO

plot( x , y ) plot( x1, y1 , x2, y2 , ... ) Graficar la función:

1 1 1
2 2 2
: : : : para segundos
: : : : :
n1 n1 : : :
n2
eje y
eje y

eje x eje x

graf2d01.m

3

EJEMPLO

plot( x1, y1, linespec1, ... ) Graficar los siguientes datos
obtenidos experimentalmente.
ƒ linespec1, es una cadena que contiene uno o mas caracteres cada uno de los cuales
representa a un especificador, los cuales pueden ser del tipo línea, del tipo marcador y/o x y
del tipo color 0.1 11.23

TIPO LÍNEA TIPO MARCADOR 0.3 12.31
0.4 14.26
Especificador Estilo de línea Especificador Tipo de Marcador
- Línea sólida (default) + Signo mas 0.7 13.44
-- Línea guión o Círculo 0.9 13.57
: Línea punteada * Asterisco 1.1 16.10
-. Línea punto-guión . Punto 1.6 15.43 graf2d02.m
x Cruz 1.9 14.56
TIPO COLOR 'square' o s Cuadrado
Especificador Color 'diamond' o d Diamante La gráfica obtenida debe tener las

r Rojo ^ Triangulo apuntando hacia arriba siguientes características:
g Verde v Triángulo apuntando hacia abajo ƒ Estilo de línea: línea sólida
b Azul > Triángulo apuntado a la derecha ƒ Marcador: cuadrado
c Cyan < Triángulo apuntando a la izquierda
ƒ Color: rojo
M Magenta 'pentagram' o p Estella de cinco puntas
Y Amarillo 'hexagram' o h Estrella de seis puntas
k Negro
w Blanco


EJEMPLO graf2d03.m
EJEMPLO

Graficar la epicicloide Graficar la siguiente función polar (cardioide)

graf2d04.m

para y ,

4

EJEMPLO

Graficar la evolución de la función polar plot( ... , 'propiedad1' , 'valor1' , ... )
ƒ Permite establecer valores a determinadas propiedades de la traza tales como:
Color, LineStyle, LineWidth, Marker, MarkerSize, MarkerEdgeColor,
para valores de
MarkerFaceColor, XData, YData, ZData, Type, etc.
graf2d05.m

plot( y1 ) plot( Y1 )
1 1
2 2
: : : : : ...
n1 n1

eje y
eje y
1 2 …… k …..……… n1 1 2 …… k …..……… n1
eje x eje x


plot( x , Y ) NOTA:
Cada vez que la función plot sea
1
2 invocada:
: : : : ... ƒ Si existen ventanas figuras presentes
n1 entonces plot trazará la(s) curva(s) y/o
conjuto(s) de muestra(s) en la última ventana
figura referenciada (utilizada) a la cual
MATLAB denomina figura actual (current
figure)
ƒ Si no existe ni una ventana figura entonces
eje y

plot creará una en la cual trazará la(s)
curva(s) y/o conjuto(s) de muestra(s).

eje x

Copyright © 2008 – ataurima@telefonica.net.pe 19
5

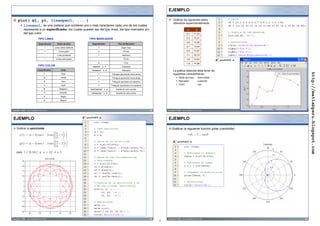
EJEMPLO graf2d06.m

Graficar los polinomios obtenidos por
el método de los mínimos
cuadrados, que se ajusten a los
siguientes datos obtenidos
experimentalmente

x y
0.1 11.23
0.3 12.31
0.4 14.26
0.7 13.44
0.9 13.57
1.1 16.10
1.6 15.43

1.9 14.56

NOTA: Considere que los valores en el eje
x representan los instantes de tiempo
(medidos en segundos) en los que se
tomaron las muestras (valores en el eje y).


Control de ejes y anotaciones

Control de ejes ƒ axis equal Anotaciones ƒ datetick(tickaxis,dateform)
ƒ axis([xmin xmax ymin ymax]) Establece la proporción entre la anchura y la altura de ƒ title('cadena') Formatea las etiquetas de las líneas tick de un eje
la traza (aspect ratio) de manera que las unidades de Muestra la cadena en la parte superior-centro del eje usando fechas, reemplazando las etiquetas numéricas
Establece los límites para los ejes x e y del actual eje.
los datos son las mismas en toda dirección. actual. por defecto. tickaxis es la cadena ‘x’, ‘y’ o ‘z’. Por
ƒ axis([xmin xmax ymin ymax zmin zmax cmin cmax])
ƒ axis image ƒ title(axes_handle,...)
defecto es ‘x’. datetick selecciona un formato de
Igual que el anterior mas los límites de escalamiento etiqueta basado en los límites mínimo y máximo de los
Funciona igual que axis equal excepto que la caja
de color Añade el titulo a los ejes especificados. ejes especificados. dateform es un entero que
de la traza se ajusta de manera ceñida alrededor de
ƒ v = axis ƒ title(... ','Propiedad',valor,...) especifica el formato de las etiqueta.
los datos.
Retorna un vector fila conteniendo los factores de ƒ axis square Funciona igual que las anteriores añadiendo la ƒ [x,y]=ginput(n)
escala de los ejes. posiblidad de especificar pares propiedad/valor. Permite seleccionar n puntos del actual eje cuyas
hace cuadrada la región del actual eje.
ƒ axis auto ƒ xlabel('cadena') coordenadas x e y son retornadas en los vectores
ƒ axis normal
Establece los límites del actual eje basándose en los ylabel('cadena') columna x e y respectivamente. Se puede finalizar el
Ajusta automáticamente el proporción de aspecto de ingreso de los puntos presionando la tecla Enter.
valores mínimos y máximos de los datos. Etiqueta los ejes x e y respectivamente.
los ejes y el escalamiento relativo de las unidades de ƒ [x,y]=ginput
ƒ axis tight dato de manera que la traza se ajuste a la forma de la ƒ legend('cadena1', 'cadena2',...)
Establece los limites de los ejes al rango de los datos figura tan bien como sea posible. Muestra una leyenda en el actual eje usando las Igual que el anterior pero permitiendo seleccionar los
puntos hasta presionar la tecla Enter.
ƒ axis ij ƒ axis off cadenas especificadas para etiquetar cada conjunto de
datos en el orden en que han sido trazados. ƒ gtext('cadena')
Establece el origen del sistema de coordenadas en la Desactiva las líneas de los ejes, marcadores tick, y
esquina superior izquierda. El eje i es vertical, con etiquetas. ƒ text(x,y,'cadena') Espera a que se presione un botón del ratón o del
teclado mientras el puntero esta dentro de la ventana
valores crecientes de arriba a abajo. El eje j es ƒ axis on Añada la cadena en la posición especificada por el
horizontal con valores crecientes de izquierda a punto (x,y), x e y deben ser números double. figura. Ubica el texto especificado por cadena en la
Activa las líneas de los ejes, marcadores tick, y posición en donde se presione un botón del ratón o
derecha
etiquetas. ƒ text(x,y,'cadena','Propiedad',valor,...)
presione cualquier tecla.
ƒ axis xy
ƒ axis(axes_handles,...) Funciona igual que la anterior añadiendo la posiblidad ƒ clabel(C,h,'Propiedad',valor,...)
Dibuja el gráfico en formato de ejes cartesianos por de especificar pares propiedad/valor.
Aplica el comando axis a ejes específicos. alterna las etiquetas e las inserta en las líneas de
defecto con el origen del sistema de coordenadas en ƒ texlabel(f)
ƒ xlim([xmin xmax]) contorno. La función inserta solo aquellas etiquetas
la esquina inferior izquierda. El eje x es horizontal con
ylim([ymin ymax]) Convierte la expresión MATLAB f en un equivalente que se ajustan al interior del contorno, dependiendo
valores crecientes de izquierda a derecha. El eje y es
TeX / LaTeX para usarlo en cadenas de texto. del tamaño del contorno. Se pueden especificar pares
vertical con calores crecientes de abajo hacia arriba. Establece los límites de los ejes en x e y
Generalmente se usa en como cadena con la función propiedad/valor
respectivamente.
text.

6

Múltiples ejes en una Ventana figura EJEMPLO

Para crear múltiples ejes en una venta Graficar las funciones
figura, o dicho de otra manera, dividir la
actual figura en ejes dispuestos en una
distribución de m filas por n columnas se
utiliza la función subplot 1 2 n-1 n para segundos
h = subplot(m,n,p)
A) En un mismo eje graf2d07.m
La cual permite elegir el objeto eje p-ésimo n+1 n+2 n+(n-1) 2n
m
como eje actual retornando un manipulador filas
de ejes h.
p

(m-1)n+1 (m-1)n+2 (m-1)n+(n-1) mn
NOTAS:
ƒ Cada eje es numerado por filas de izquierda a
derecha a partir de 1 hasta mn.

ƒ Cada vez que se especifica un eje actual, toda n
ejecución de algún comando de graficación, por columnas
ejemplo plot, se ejecutará en dicho eje.

subplot(m,n,p)
plot(x,y)


B) En ejes independientes: t vs.x, t vs.y C) En ejes independientes: t vs.x, t vs.y, x vs.y
graf2d09.m
graf2d08.m

7

EJEMPLO Universidad Nacional de Ingeniería
Facultad de Ingeniería Eléctrica y Electrónica MATLAB
Graficar , donde graf2d10.m
Lima – Perú NIVEL BÁSICO

para y
con particiones. Gráficas Tridimensionales

Funciones trazadoras de Gráficas Tridimensionales.
Gráfica de muestras tridimensionales
Gráfica de curvas tridimensionales.

Gráfica de superficies tridimensionales.
Ejemplos con funciones para el trazado de muestras tridimensionales.
Ejemplos con funciones para el trazado de curvas tridimensionales.
Ejemplos con funciones para el trazado de superficies tridimensionales R2 a R.
Ejemplos con funciones para el trazado de superficies tridimensionales R2 a R3.

EXPOSITOR: http://matlabperu.blogspot.com
Miguel Ataurima Arellano ataurima@telefonica.net.pe
INGENIERO CONSULTOR
ma2lac@msn.com 30
Copyright © 2008 – ataurima@telefonica.net.pe 29

Funciones Gráficas Tridimensionales Gráfica de muestras tridimensionales

Se deben seguir los siguientes pasos:
Linea ƒ Se debe especificar el dominio de graficación a través de vectores.

x = [1 3 5 8 6 4 2];
Malla y = [2 4 5 7 6 4 1];
y Barra y = [2 6 7 8 9 10 12];

Área ƒ Con estos vectores se efectúa la gráfica de las muestras haciendo usando las funciones
y objetos MATLAB para el trazado tridimensional
constructivos
stem3(x,y,z) scatter3(x,y,z)

Superficie
15 15

10 10

Dirección
5 5

0 0
12 8
12
Volumétrico 10
8
6 10 6
8

6 4 8
2 6 4
4
2 0 4 2
2 0

8

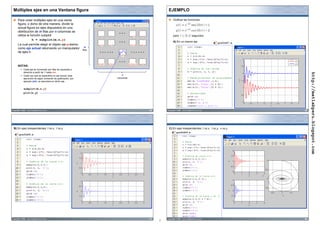
Gráfica de curvas tridimensionales Gráfica de superficies tridimensionales

Se deben seguir los siguientes pasos: Se deben seguir los siguientes pasos:
ƒ Especificar el dominio de la variable t =
independiente (por lo general, tiempo). 0 0.3142 ... 31.1018 31.4159 ƒ Transformar los vectores dominios a
arreglos bidimensionales a través de la
t = 0:pi/10:10*pi; función meshgrid.
x =
0 0.0971 ... -9.6110 -0.0000
ƒ Generar los vectores dominio a través Dx = -3:3;
de alguna regla de correspondencia con y = Dy = -2:2;
la variable independiente. 0 0.2988 ... 29.5795 31.4159
[x,y] = meshgrid(Dx,Dy);
z =
x = t.*sin(t); 0 0.0987 ... 967.3199 986.9604 ƒ Estas matrices serán usadas para evaluar
y = t.*cos(t); las funciones y luego graficarlas usando
z = t.^2; las funciones MATLAB de trazado de

superficies/mallas tridimensionales.
ƒ Graficar la curva descrita por los
400
Gráfica de la curva
300
vectores obtenidos en el paso anterior z = x.^2 + y.^2; 15

usando las funciones MATLAB para el 200
surf(x,y,z); 10
trazado de curvas tridimensionales 100
Gráfica de la función
5
0
20
10 20
plot3(x,y,z); 0 10
0
2
0 1 4
-10 -10
0 2
-20 -20 0
-1 -2
-2 -4


EJEMPLO EJEMPLO

Graficar la curva definida por Graficar la función sinc dada por

curva3d1.m

para
para

40
misinc.m

20
eje Z

0
1
1
0
0

eje Y -1 -1
eje X

9

EJEMPLO EJEMPLO

Graficar la función sinc levantando la intederminación en (0,0) Graficar la superficie

misinc1.m discontinuidad

para y
además 20 curvas de nivel

graf3d1.m

misinc2.m


EJEMPLO EJEMPLO

Graficar la función Graficar el campo vectorial (gradiente) de la función

4

con separaciones en y de 0.5 en [-2,2] para todo x [-3,3] para 3

graf3d2.m 2
graf3d3.m

1

0

-1

-2

-3

-4
-2 -1 0 1 2

10

EJEMPLO EJEMPLO

Graficar los vectores normales a la superficie Efectuar la gráfica de un toroide circular

graf3d4.m
Ecuaciones paramétricas

para

Z

0 (x,y,z)

a u r
Y
v

X


EJEMPLO

Efectuar la gráfica de la banda de Möbius
mitoroide.m

para ,
mobius.m

11

EJEMPLO

Graficar en forma superpuesta las siguientes superficies paramétricas graf3d5.m

Paraboloide Esfera


12

Matlab sesion3

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Matlab sesion3

Más de José Caraguay

Último

Matlab sesion3