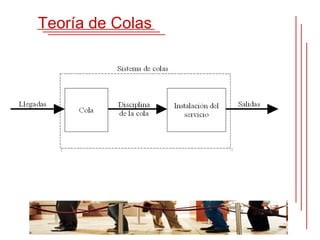
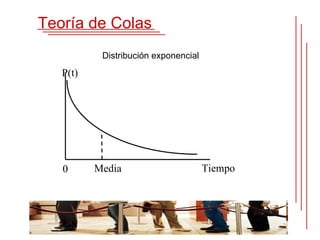
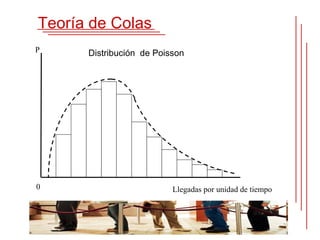
La teoría de colas estudia matemáticamente el comportamiento de las líneas de espera. Se forma una cola cuando los clientes llegan a un servidor compartido demandando servicio. La teoría de colas provee modelos para predecir el comportamiento de sistemas de colas y encontrar un balance entre los costos y tiempos de espera. El matemático danés Agner Krarup Erlang publicó el primer artículo sobre la teoría de colas en 1909 para estudiar el dimensionamiento de sistemas telefónicos.

1. Teoría de Colas
Las "colas" son un aspecto de la vida moderna que
nos encontramos continuamente en nuestras actividades
diarias. En el contador de un supermercado, en los Bancos,
entre otros, el fenómeno de las colas surge cuando unos
recursos compartidos necesitan ser accedidos para dar
servicio a un elevado número de trabajos o clientes.

2. Teoría de Colas
El estudio de las colas es importante porque
proporciona tanto una base teórica del tipo de servicio que
podemos esperar de un determinado recurso, como la forma
en la cual dicho recurso puede ser diseñado para
proporcionar un determinado grado de servicio a sus clientes.

3. Teoría de Colas
El matemático danés Agner Krarup Erlang, trabajador
de la Copenhagen Telephone Exchange, publicó el primer
artículo sobre la teoría de colas en 1909. Específicamente se
preocupó del estudio del problema de dimensionamiento de
líneas y centrales de conmutación telefónica para el servicio
de llamadas.

4. Teoría de Colas
La teoría de colas es el estudio matemático del
comportamiento de líneas de espera.
Esta se presenta, cuando los "clientes" llegan a un
"lugar" demandando un servicio a un "servidor", el cual tiene
una cierta capacidad de atención. Si el servidor no está
disponible inmediatamente y el cliente decide esperar,
entonces se forma la línea de espera.

5. Teoría de Colas
Una cola es una línea de espera y la teoría de colas
es una colección de modelos matemáticos que describen
sistemas de línea de espera particulares o sistemas de colas.
Los modelos sirven para encontrar un buen compromiso entre
costes del sistema y los tiempos promedio de la línea de
espera para un sistema dado.

6. Teoría de Colas
En la teoría de la formación de colas, generalmente
se llama sistema a un grupo de unidades físicas, integradas
de tal modo que pueden operar al unísono con una serie de
operaciones organizadas.
La teoría de la formación de colas busca una solución
al problema de la espera prediciendo primero el
comportamiento del sistema.

7. Teoría de Colas
Pero una solución al problema de la espera consiste
en no solo en minimizar el tiempo que los clientes pasan en el
sistema, sino también en minimizar los costos totales de
aquellos que solicitan el servicio y de quienes lo prestan.
Se debe lograr un balance económico entre el costo
del servicio y el costo asociado a la espera por ese servicio.
La teoría de colas en sí no resuelve el problema, sólo
proporciona información para la toma de decisiones.

8. Teoría de Colas
Los objetivos de la teoría de colas consisten en:
* Identificar el nivel óptimo de capacidad del sistema que
minimiza el coste del mismo.
* Evaluar el impacto que las posibles alternativas de
modificación de la capacidad del sistema tendrían en el coste
total del mismo.
* Establecer un balance equilibrado (“óptimo”) entre las
consideraciones cuantitativas de costes y las cualitativas de
servicio.
* Prestar atención al tiempo de permanencia en el sistema
o en la cola de espera.
En general el objetivo es encontrar el estado estable
del sistema y determinar una capacidad de servicio
apropiada.

9. Teoría de Colas
Un sistema de colas puede dividirse en dos
componentes principales:
•La cola
•La instalación del servicio
Los clientes o llegadas vienen en forma individual para recibir
el servicio.
Los clientes o llegadas pueden ser:
–Personas
–Automóviles
–Máquinas que requieren reparación
–Documentos
–Entre muchos otros tipos de artículos

10. Teoría de Colas
Si cuando el cliente llega no hay nadie en la cola,
pasa de una vez a recibir el servicio; si no, se une a la cola.
Es importante señalar que la cola no incluye a quien está
recibiendo el servicio.
Las llegadas van a la instalación del servicio de
acuerdo con la disciplina de la cola.
Generalmente ésta es primero en llegar, primero en ser
servido.
Pero pueden haber otras reglas o colas con prioridades.

11. Teoría de Colas

12. Teoría de Colas
•El número de clientes en la cola es el número de clientes que
esperan el servicio.
•El número de clientes en el sistema es el número de clientes
que esperan en la cola más el número de clientes que
actualmente reciben el servicio.
•La capacidad de la cola es el número máximo de clientes que
pueden estar en la cola.
Generalmente se supone que la cola es infinita,
aunque también la cola puede ser finita.
•La disciplina de la cola se refiere al orden en que se
seleccionan los miembros de la cola para comenzar el
servicio.

13. Teoría de Colas
Costo de espera: Es el costo para el cliente al esperar,
representa el costo de oportunidad del tiempo perdido.
Un sistema con un bajo costo de espera es una
fuente importante de competitividad.
Costo de servicio: Es el costo de operación del servicio
brindado.
Es más fácil de estimar.

14. Teoría de Colas
El objetivo de un sistema de colas es encontrar el
sistema del costo total mínimo.
•El tiempo que transcurre entre dos llegadas sucesivas en el
sistema de colas se llama tiempo entre llegadas.
•El tiempo entre llegadas tiende a ser muy variable.
•El número esperado de llegadas por unidad de tiempo se
llama tasa media de llegadas (λ).
•El tiempo esperado entre llegadas es 1/λ
Por ejemplo, si la tasa media de llegadas es λ = 50
clientes por hora.
Entonces el tiempo esperado entre llegadas es 1/λ =
1/50 = 0.02 horas o 1 minutos.

15. Teoría de Colas
Además es necesario estimar la distribución de
probabilidad de los tiempos entre llegadas.
Generalmente se supone una distribución
exponencial
Esto depende del comportamiento de las llegadas.
La forma algebraica de la distribución exponencial es:
P(tiempo de servicio ≤ t ) = 1 − e − µt
Donde t representa una cantidad expresada en de tiempo
unidades de tiempo (horas, minutos, etc.)

16. Teoría de Colas
Distribución exponencial
P(t)
0 Media Tiempo

17. Teoría de Colas
La distribución exponencial supone una mayor
probabilidad para tiempos entre llegadas pequeños.
En general, se considera que las llegadas son aleatorias.
La última llegada no influye en la probabilidad de llegada de la
siguiente.

18. Teoría de Colas
P Distribución de Poisson
0 Llegadas por unidad de tiempo

19. Teoría de Colas
La Distribución de Poisson es una distribución
discreta empleada con mucha frecuencia para describir el
patrón de las llegadas a un sistema de colas.
Para tasas medias de llegadas pequeñas es
asimétrica y se hace más simétrica y se aproxima a la
binomial para tasas de llegadas altas.
Su forma algebraica es: λk e − λ
P (k ) =
k!
Donde:
P(k) : probabilidad de k llegadas por unidad de tiempo
λ : tasa media de llegadas
e = 2,7182818…