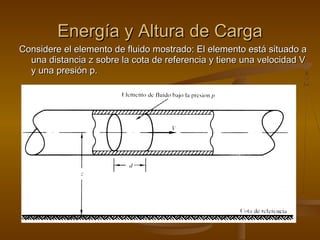
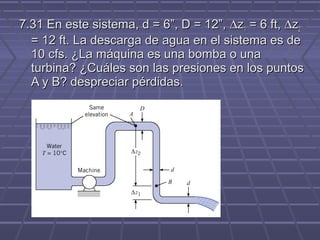
El documento describe las diferentes formas de energía que pueden poseer los fluidos en movimiento, incluyendo la energía potencial, cinética y de presión. Explica la ecuación de la energía total para fluidos incompresibles y su equivalencia a la altura de carga. También presenta el teorema de Bernoulli y su aplicación para resolver problemas de mecánica de fluidos. Finalmente, incluye ejemplos resueltos de aplicación del teorema.

1. Cont. CAPITULO 6
Energía Y Altura de Carga
 La energía se define como la capacidad de
realizar un trabajo. El trabajo resulta de aplicar
una fuerza a lo largo de cierto recorrido (F*d). Se
expresa en Joules (1J = 1Nm), o lb-ft.
 Los fluidos en movimiento poseen energía.
Aparece en tres formas distintas:
1) Energía Potencial.
2) Energía Cinética.
3) Energía de Presión.

2. Energía y Altura de Carga
Considere el elemento de fluido mostrado: El elemento está situado a
una distancia z sobre la cota de referencia y tiene una velocidad V
y una presión p.

3.  Energía potencial: Se refiere a la energía que posee el
elemento de fluido debido a su elevación respecto de la cota de
referencia. La energía potencial (PE) viene dada por:
PE = W*z
 Energía Cinética: es la energía que posee el elemento debido
a su velocidad. La energía cinética (KE) viene dada por:
KE = m*V2/2 = W*V2/2g
 Energía de Presión: es llamada también energía de flujo. Es
la cantidad de trabajo que se requiere para forzar al fluido a
moverse cierta distancia contra la presión. La energía de flujo
viene dada por:
FE = F*d = p*A*d
Vol = A*d = W/γ
Por lo tanto: FE = p*W/γ

4. Energía y Altura de Carga
 La energía total (E): Es la suma de PE, KE y FE, es decir,
E = W*z + W*V2/2g + W*p/γ
 En los problemas de mecánica de fluidos y de hidráulica es
conveniente manejar la energía como carga, es decir cantidad
de energía por unidad de peso del fluido. (J/N = m)
 Al expresar la energía total como altura de carga (H)
obtenemos (dividiendo todos los términos por W):
H = z + v2/2g + p/γ
Donde z es la cota topógráfica, a v2/2g se le llama altura de
velocidad y p/γ es la altura de presión, todo en metros o pies.

5. Ecuación de la Energía
 Se obtiene la ecuación de la energía al aplicar al flujo
fluido el principio de conservación de la energía, la cual
se aplica en la dirección del flujo:
E. en (1) + E. añadida – E. extraída – E. perdida = E. en (2)
 Esta ecuación es para flujos incompresibles,
permanentes con variaciones en su energía interna
despreciables. Se reduce a:
(P1/γ + V12/2g + z1) + HA – HL – HE = (p2/γ + V22/2g + z2)
TEOREMA DE BERNOULLI

6. Altura de Velocidad
 La altura de velocidad representa la energía cinética por
unidad de peso que existe en un punto específico, si la
velocidad en una sección fuera uniforme (variaciones
despreciables), el cálculo de la altura de velocidad podría
determinarse a partir de la velocidad media sin producirse
errores significativos.
 Por lo general la distribución de velocidades no es uniforme,
se debe integrar las energías cinéticas diferenciales. El factor
de corrección (α) por el que hay que multiplicar Vmedia2/2g viene
dado por:
α= 1/A f (v/V)3 dA
A
Donde V = Velocidad media,
v = velocidad en un punto.

7. Altura de Velocidad
 Para velocidades uniformes α = 1.0.
 Para flujos turbulentos α = 1.02 – 1.15.
 Para flujos laminares α = 2.0.
 En los problemas de mecánica de fluidos por lo general
se toma α = 1 debido a que la altura de velocidad
representa un pequeño porcentaje de la altura de carga
total.

8. Aplicación del Teorema de
Bernoulli
1) Dibujar un esquema.
2) Aplicar la ecuación en dirección del flujo, seleccionar
nivel de referencia.
3) Si las dos alturas de velocidad son desconocidas,
relacionarlas con la ecuación de continuidad. (Q = A1V1
= A2V2)
4) Utilizar presiones absolutas o manométricas siempre y
cuando se mantenga el tipo de presión en todos los
puntos.
5) Restar las alturas de carga que extraen las turbinas y
las que representan energía perdida, agregar las
suministradas por las bombas.

9. Ejemplos
7.16 Un depósito con agua se encuentra presurizado como
se muestra. El diámetro del tubo es de 1”. La pérdida de
carga en el sistema está dada por hL = 5v2/2g. La altura
entre la superficie del agua y el tubo es 10 ft. Se hace
necesaria una descarga de 10 ft3/s. ¿Cuál debe ser la
presión en el tanque para alcanzar este caudal?

10. Escribir la ecuación de la energía desde la superficie de agua en el
depósito (punto 1) hacia la descarga (punto 2):
(P1/γ + V12/2g + z1) + HA – HL – HE = (p2/γ + V22/2g + z2)
Consideraciones especiales en el punto 1:
- La presión es igual a la presión que ejerce el aire.
- La velocidad se toma como cero debido a que es despreciable la
velocidad a la que bajan de nivel los depósitos al compararlas
con las velocidades adentro de las tuberías (V 1 = 0).
Consideraciones especiales en el punto 2:
- La presión manométrica es cero porque se toma el dato en el
punto justo al salir del tubo, la cual es atmosférica (p 2 = 0).
- Por ser el punto más bajo, se elige como nivel de refencia, z 2 = 0.
Otras consideraciones:
- Al no haber bombas HA = 0, al no haber turbinas HE = 0.

11. Al simplificar la ecuación haciendo cero los valores apropiados:
(P1/γ + V12/2g + z1) + HA – HL – HE = (p2/γ + V22/2g + z2)
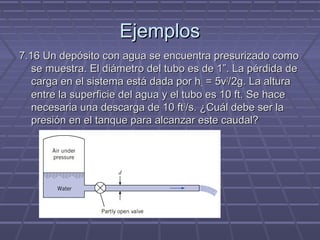
Z1 = 10 ft
V2 = Q/A = 0.10/(π (1/12)2/4) = 18.33 ft/s
HL = 5 V2/2g
Entonces:
P1/(62.4) + 0 + 10 + 0 - 5 (18.33)2/2g – 0 = 0 + (18.33)2/2g + 0
P1 = [6 (18.33)2/2g -10]*62.4 = 1329 psfg = 9.23 psig

12. 7.26 La descarga en el
sifón es de 2.8 cfs, D
= 8”, L1 = 3 ft, L2 = 3 ft.
Determinar la pérdida
de carga entre el
depósito y el punto C.
Determinar la presión
en B si ¾ de la
pérdida de carga se
da entre la superficie
del depósito y B.

13. Escribir la ecuación de la energía desde la superficie de agua en el
depósito (punto 1) hacia la descarga (punto 3) debido a que son
los puntos con menos incógnitas:
(P1/γ + V12/2g + z1) + HA – HL – HE = (p3/γ + V32/2g + z3)
Consideraciones especiales en el punto 1:
- La presión manométrica es cero porque es la atmosférica.
- La velocidad se toma como cero debido a que es despreciable la
velocidad a la que bajan de nivel los depósitos al compararlas
con las velocidades adentro de las tuberías (V 1 = 0).
Consideraciones especiales en el punto 3:
- La presión manométrica es cero porque se toma el dato en el
punto justo al salir del tubo, la cual es atmosférica (p 3 = 0).
- Por ser el punto más bajo, se elige como nivel de refencia, z 3 = 0.
Otras consideraciones:
- Al no haber bombas HA = 0, al no haber turbinas HE = 0.

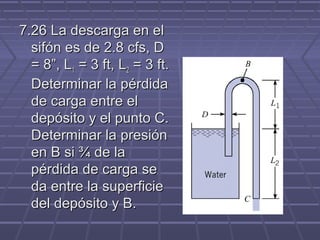
14. Al simplificar la ecuación haciendo cero los valores apropiados:
(P1/γ + V12/2g + z1) + HA – HL – HE = (p3/γ + V32/2g + z3)
Z1 = 3 ft
V3 = Q/A = 2.8/(π (8/12)2/4) = 8.02 ft/s
HL = ?
Entonces:
0 + 0 + 3 + 0 - HL – 0 = 0 + (8.02)2/2g + 0
HL = [-(8.02)2/2g + 3] = 2 ft

15. Para el siguiente paso se aplica la ecuación de la energía desde la
superficie de agua en el depósito (punto 1) el punto B del sifón
(punto 2) debido a que ya se sabe la pérdida entre los puntos:
(P1/γ + V12/2g + z1) + HA – HL – HE = (p2/γ + V22/2g + z2)
Consideraciones especiales en el punto 2:
- La presión manométrica no es cero.
- La velocidad es la misma a lo largo de todo el tubo debido a que
el diámetro no cambia. (V2 = 8.02 ft/s).
- La cota desde el nivel de referencia es z2 = 6 ft
Otras consideraciones:
- Al no haber bombas HA = 0, al no haber turbinas HE = 0.
- La pérdida de carga entre 1 y 2 es ¾(2ft) = 1.5 ft

16. Al simplificar la ecuación haciendo cero los valores apropiados:
(P1/γ + V12/2g + z1) + HA – HL – HE = (p2/γ + V22/2g + z2)
Entonces:
0 + 0 + 3 + 0 – 1.5 – 0 = p2/62.4 + (8.02)2/2g + 6
P2 = -343 psfg = - 2.38 psig

17. 7.31 En este sistema, d = 6”, D = 12”, ∆z1 = 6 ft, ∆z2
= 12 ft. La descarga de agua en el sistema es de
10 cfs. ¿La máquina es una bomba o una
turbina? ¿Cuáles son las presiones en los puntos
A y B? despreciar pérdidas.

18. Escribir la ecuación de la energía desde la superficie de agua en el
depósito (punto 1) hacia la descarga (punto 3) debido a que son
los puntos con menos incógnitas:
(P1/γ + V12/2g + z1) + HA – HL – HE = (p3/γ + V32/2g + z3)
Consideraciones especiales en el punto 1:
- La presión manométrica es cero porque es la atmosférica.
- La velocidad se toma como cero debido a que es despreciable la
velocidad a la que bajan de nivel los depósitos al compararlas
con las velocidades adentro de las tuberías (V 1 = 0).
Consideraciones especiales en el punto 3:
- La presión manométrica es cero porque se toma el dato en el
punto justo al salir del tubo, la cual es atmosférica (p 3 = 0).
- Por ser el punto más bajo, se elige como nivel de refencia, z 3 = 0.
Otras consideraciones:
- La máquina desconocida se tomará solo como H y HL = 0.

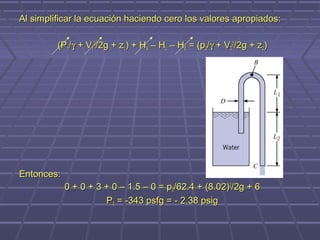
19. Al simplificar la ecuación haciendo cero los valores apropiados:
(P1/γ + V12/2g + z1) + H – HL = (p3/γ + V32/2g + z3)
Z1 = 6 + 12 = 18 ft
V3 = Q/A = 10/(π (6/12)2/4) = 50.95 ft/s
H=?
Entonces:
0 + 0 + 18 + H - 0 = 0 + (50.95)2/2g + 0
H = [(50.95)2/2g - 18] = 22.31 ft (BOMBA)

20. HOJA DE TRABAJO
Encontrar las presiones en A y B.