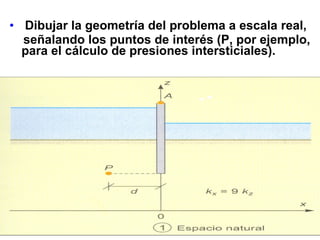
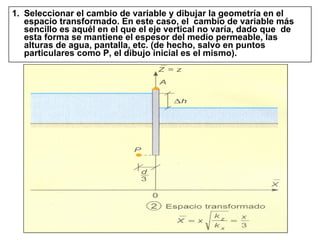
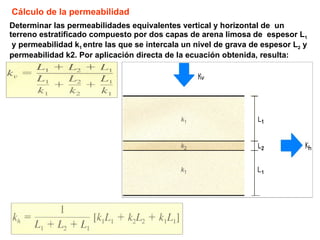
El documento describe los métodos y aplicaciones de la ingeniería geológica. Se basa en la geología y el comportamiento mecánico de suelos y rocas. Incluye técnicas de investigación del subsuelo e instrumentales, así como métodos de análisis y modelado. Siguiendo un proceso metodológico, se identifican materiales, estructuras, litología y condiciones hidrogeológicas. Luego se caracterizan propiedades de los materiales y se evalúa su comportamiento mecánico e hidrá