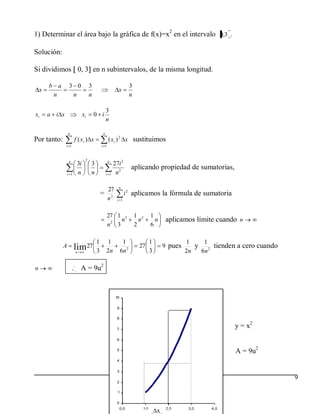
Este documento trata sobre el cálculo de integrales definidas. Explica que los matemáticos griegos intentaron calcular el área bajo curvas, y que Arquímedes desarrolló el método de agotamiento. Luego introduce la notación sigma para sumatorias y presenta propiedades y fórmulas útiles para calcular sumas. Finalmente, explica cómo usar sumatorias para aproximar el área bajo una curva.

1. LA INTEGRAL DEFINIDA
Uno de los grandes problemas que ocupó a los matemáticos griegos de la antigüedad fue
el de la comparación de figuras curvilíneas y rectilíneas.
Durante mas de 2,000 años los griegos abordaron el problema de calcular áreas de
regiones limitadas por curvas, destacándose entre ellos el método empleado por
Arquímedes llamado método de exhaución. Dicho método consiste en inscribir polígonos
regulares y calcular su área, repetir el proceso varias veces duplicando el número de lados
de los polígonos, hasta llegar a un valor que se consideraba que representaba el área de la
región.
3 b
1
6x 2 5 dx 45 f med f ( x)dx
2
b a a
9
t 3 20
dt
4 t 3
INTEGRAL DEFINIDA
En esta unidad trataremos con sumas de muchos términos, por lo cual introducimos una
notación llamada notación sigma para facilitar la escritura de estas sumas.
Esta notación incluye el uso del símbolo , la sigma mayúscula del alfabeto griego que
corresponde a nuestra letra S.
5
Ej: i2 12 22 32 42 52
i 1
1

2. 2
(3i 2) 3 2 2 3 1 2 30 2 31 2 32 2
i 2
-4 - 1 + 2 +5 +8 = 10
8
1 1 1 1 1 1 1
k 3 k 3 4 5 6 7 8
n f (i ) f ( m) f (m 1) f (m 2) ....... f ( n)
En General:
i m
Donde m y n son entero y m ≤ n
El número m se llama límite inferior de la suma y n se llama el límite superior. El
símbolo i se llama el índice de la suma, es un símbolo arbitrario porque se puede usar
cualquier letra.
Por Ejemplo:
5
t2 32 42 52
t 3
En ocasiones los términos de la suma incluyen subíndices como:
n
a) Ai A1 A2 .... An
i 1
9
b) kbk 4b4 5b5 6b6 7b7 8b8 9b9
K 4
5
c) f ( xi ) X f ( x1 ) x f ( x2 ) x2 f ( x3 ) 3 f ( x4 ) 4 f ( x5 ) 5
i 1
Propiedades de la Sumatoria
n
Propiedad 1. c cn donde c es cualquier constante.
i 1
n n
Propiedad 2. c. a ( i ) c a i donde c es cualquier constante.
i 1 i 1
n n n
Propiedad 3. a +b ]=
i i a + i bi
i 1 i 1 i 1
2

3. n n
Si ai = a (una constante) entonces a bi na bi
i 1 i 1
n
Propiedad 4. a( i )-a(i-1) = a( n ) – a( 0 )
i 1
La suma de las k-ésima potencias de los primeros n enteros positivos
n
ik 1k 2k 3k .... n k
i 1
Las siguientes fórmulas relativas a las sumatorias también son útiles.
n
n(n 1) 1 2 1
1) i n n
i 1 2 2 2
n
n(n 1)( 2n 1) 1 3 1 2 1
2) i2 n n n
i 1 6 3 2 6
n
3 n 2 (n 1) 2 1 4 1 3 1 2
3) i n n n
i 1 4 4 2 4
Ejemplo
n
1) Calcular (4 i 4 i 1 ) sustituimos los superíndices de la propiedad 4.
i 1
n
4i 4i 1
4n 41 1
i 1
= 4n 40
= 4n 1
20
2) Calcular 3k ( k 2 2)
k 1
3

4. 20
Soluc. 3 k (k 2 2) propiedad 2
k 1
20
3 k3 2K
k 1
20 20
3 k3 2k propiedad 3
k 1 k 1
2
20 2 20 1 20 20 1
3 2 Usando fórmulas 3 y 1 y calculadora.
4 2
2
400 21
3 420
4
3 44100 420
R = 133560
1 2 3 .... n
3) Evalúe el límite lim n n2
n
nn 1
i
Solución: Usamos la fórmula i 1 2
1
nn 1
1 2 3 .... n 2 n 1
lim
n n2 lim n 2
n
lim
n 2n
n 1 1 1 1
lim
n 2n 2n lim
n 2 2n 2
1
Ya que 2n tiende a cero cuando n
Ejercicios Propuestos
4

5. Calcular la suma indicada, usando propiedades y/o fórmulas:
25
R/ 10,400
2i i 1
a) i 1
20
R/ 133,560
3i i 2 2
b) i 1
100
1 1 R/ 100/101
c) ik 11 k k 1
40
2i 1 2i 1 1 81
d) R/
i 11
8
R/ -32
5 2j
e) j 1
100
R/ 25,502,500
i3
f) i 1
8
R/ 224
r 1 r 2
g) r 1
Área por Sumatorias o Suma de Áreas
Es fácil calcular el área de una región plana cuando está limitada por líneas. Por ejemplo,
si la región es un rectángulo, un triángulo o cualquier polígono que se pueda dividir en
triángulos, existen fórmulas que permiten determinar su área:
5

6. Para encontrar área de regiones cuyos límites no son rectas sino gráficas de funciones, es
necesario utilizar un proceso que se fundamenta en le concepto de límite.
La siguiente figura muestra la región R que está bajo la gráfica de una función creciente f,
con valores positivos, y por arriba del intervalo a, b . Para aproximar el área A de R,
elegimos un entero fijo n y dividimos el intervalo a, b en n intervalos.
b a
x0, x1 , x1, x2 , x2 , x3 , …, xn-1 , xn todos con la misma longitud x . En cada
n
uno de estos intervalos, levantamos un rectángulo inscrito y un rectángulo circunscrito
(figura1)
y
y = f(x)
Figura 1
f (b) – f (a)
6

7. x x
a = x0 x1 x2 x3 xn-1 xn= b
Una función f continua y no negativa tiene área bajo su grafica si cuando la amplitud de
su partición x tiende a cero, entonces el límite de las aproximaciones por exceso es
igual al límite de las aproximaciones por defecto.
El rectángulo inscrito sobre el i-esimo termino sub intervalo xi-1, xi tiene altura f (xi-1),
mientras que el i-esimo rectángulo circunscrito tiene una altura f(xi). Como la base de
cada rectángulo tiene una longitud x las áreas de estos rectángulos son f (xi-1) x y
f (xi) x.
y
f(xi)
f (xi-1)
x
a=x0 xi-1 xi xn=b
7

8. Al sumar las áreas de los rectángulos inscritos para i = 1, 2, 3 ….. n obtenemos la
n
An f xi 1 x
subestimación i 1 del área real A
De manera análoga la suma de las áreas de los rectángulos circunscritos es la
n
An f xi x
sobreestimación i 1
n n
f xi 1 x A f xi x
La desigualdad implica que An A An , entonces i 1 i 1
Las desigualdades se invierten si f` x fuera decreciente. Si el número n de
subintervalos es muy grande, de modo que x sea muy pequeño, entonces la
diferencia entre las áreas An y An de los polígonos inscritos y circunscritos será
muy pequeña. Por tanto ambos valores serán muy cercanos al área real A de la
región R.
An An f b f a
Pero b a , cuando
0 n
n
El área de la región R está dada por:
n n
A lim f xi 1 lim f xi x
n i 1 n i 1
b a
Al aplicar la fórmula o Ecuación recordemos que x y x1 a i x para i=0, 1, 2,
n
…..n pues xi está a i pasos de longitud x a la derecha de 0 a
Ejemplos.
8

9. 1) Determinar el área bajo la gráfica de f(x)=x2 en el intervalo 0,3 .
Solución:
Si dividimos 0, 3 en n subintervalos, de la misma longitud.
b a 3 0 3 3
x x
n n n n
3
xi a i x xi 0 i
n
n n
Por tanto: f ( xi ) x ( xi ) 2 x sustituimos
i 1 i 1
2
n
3i 3 n
27i 2
2
aplicando propiedad de sumatorias,
i 1 n n i 1 n
n
27
= i 2 aplicamos la fórmula de sumatoria
n2 i 1
27 1 3 1 2 1
n n n aplicamos límite cuando n
n2 3 2 6
1 1 1 1 1 1
A lim 27 27 9 pues y 2 tienden a cero cuando
n 3 2n 6n 2 3 2n 6n
n ... A = 9u2
10
9
8
7
y = x2
6
5
A = 9u2
4
3
9
2
1
0
0,0 1,0 2,0 3,0 4,0
x

10. Ejemplo:
2) Determine el área bajo la gráfica de f(x):100-3x2 de x=1 a x=5
Solución: El intervalo es 1 , 5
b a 5 1 4
x
n n n
xi a i x
4 4i
xi 1 i xi 1 Ahora apliquemos la fórmula
n n
n n
f x x 100 3x 2 x
i 1 i 1
n 2
4i 4
100 31
i 1 n n
n
8i 16i 2 4
100 3 1
i 1 n n2 n
n
24i 48i 2 4
100 3
i 1 n n2 n
n
24 i 48 i 2 4
97
i 1 n n2 n
n
388 96i 192i 2
i 1 n n2 n3
10

11. n n n
388 96 192
1 i i2
n i 1 n2 i 1 n3 i 1
aplicamos fórmulas correspondientes a cada caso.
n n
388 96 1 2 1 192 1 3 1 2 1
f x x 100 3x 2 x n n n n n n
i 1 i 1 n n2 2 2 n3 3 2 6
48 96 32
Simplificamos (n) 388 48 64
n n n2
144 32
276 -
n n2
Aplicamos límite
144 32
A lim
n
276
n n3
276
A=276 u2
GRAFICA
Ejercicios Propuestos
Determine exactamente el área A, de la región bajo y=f(x)
11

12. a) f x x3 en 0,3 R/ 81 u2
4
b) f x x 2 en 0,2 R/ 6u2
c) f x 5 3x en 0,1 R/ 7 u2
2
d) f x 9 x2 en 0,3 R/ 18 u2
SUMAS DE RIEMANN
n n
Las sumas de aproximación en la ecuación f xi 1 x y f xi x son ambas de la
i 1 i 1
n
*
forma f xi * x donde xi es un punto seleccionado en el iésimo subintervalo xi 1 , xi
i n
a = x0 x1* x1 *
x2 x2 …… xi-1 x i* xi *
xn xn = b
Una función f definida en a , b que no necesariamente es continua o positiva. Una
partición P de a , b es una colección de subintervalos
x0, x1 , x1, x2 , x2, x3 ,…. xn-1, xn de a , b de modo que a = x0 x1 x2 x3 ….. xn-
1 xn = b
12

13. La NORMA de la partición P es el máximo de las longitudes xi xi xi 1 de los
subintervalos en P y se denota P .
n
*
Para obtener una suma como f xi x , necesitamos un punto xi * en el iésimo
i 1
subintervalo para cada i, 1 i n. Una colección de puntos S xi *, x2* , x3* ,.....xn* donde
xi *, en xi 1 , xi (para cada i) es una selección para la partición P.
Esto define la suma de Riemann para una función f en un intervalo a , b , S una
n
*
selección para P, entonces la suma de Riemamn R f xi xi
i 1
En la siguiente gráfica de la función f x 2 x3 6x2 5 en el intervalo 0, 3
6,0
Suma según los extremos
izquierdos
4,0
n
R f xi 1 x
2,0
i 1
F(x)
0,0
-2,0
-4,0
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
,00
,10
,20
,30
,40
,50
,60
,70
,80
,90
1,00
1,10
1,20
1,30
1,40
1,50
1,60
1,70
1,80
1,90
X
Según los extremos derechos Según los puntos medios
n n
xi xi
R= f ( xi ) x Rmed = f ( mi ) x , xi* mi 1
i 1 i 1 2
13

14. 6,0 6,0
4,0 4,0
2,0 2,0
F(x)
F(x)
0,0 0,0
-2,0 -2,0
-4,0 -4,0
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
,00
,10
,20
,30
,40
,50
,60
,70
,80
,90
1,00
1,10
1,20
1,30
1,40
1,50
1,60
1,70
1,80
1,90
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
,00
,10
,20
,30
,40
,50
,60
,70
,80
,90
1,00
1,10
1,20
1,30
1,40
1,50
1,60
1,70
1,80
1,90
X X
LA INTEGRAL DEFINIDA SEGÚN RIEMANN
El matemático alemán G . F. B Riemann (1826 -1866) Proporcionó una definición
rigurosa de la integral.
Definición: La integral definida de la función f de a a b es el número
n
*
I lim
p 0 i 1
f xi xi
Siempre que el límite exista, en cuyo caso decimos que f es integrable en [a, b]. La
ecuación significa que, para cada número > 0, existe un número > 0 tal que
n
*
I f xi xi <
i 1
Para cada suma de Riemann asociada con una partición arbitraria P de [a, b] para la que
P <
Nota: La palabra límite se usa para denotar el número mínimo y el número máximo del
intervalo [a, b] y no tiene nada que ver con las definiciones de límite dadas anteriormente.
La notación usual para la integral de f de a a b, debida al filósofo y matemático alemán G.
W Leibniz, es:
14

15. Esta notación integral no solo es altamente sugerente, sino que también es útil, en
extremo para el manejo de las integrales. Los números a y b son el limite inferior y el
limite superior de la integral, respectivamente, son los extremos del intervalo de
integración.
La variable x se puede reemplazar por cualquier otra variable sin afectar el significado de
la Ecuación.
Así si f es integrable en [a, b] , entonces
b b
b
f x dx f t dt f u du ; f x es el integrando.
a
a a
La integral dada, de la integral definida, se aplica solamente cuando a < b, pero es
conveniente incluir, cuando a > b y a = b.
b
* Si a = b f x dx 0
a
b a
* Si a > b f x dx f x dx
a b
b
Definición: Se llama integral definida entre a y b de f(x), y se denota f x dx al área de
a
la porción del plano limitado por la grafica de la función f(x), el eje x y las rectas x = a y
x = b.
TEOREMA DE EVALUACIÓN DE INTEGRALES
“ Si G es una primitiva de la función continua f en G(b) – G(a) se abrevia generalmente [
b
b
G(x) ]a entonces f x dx Gb Ga
a
Ejemplo: Evaluar
15

16. 1) senxdx cosx 0 cos cos0
0
= - (-1) – (-1)
= +1 + 1 = 2
2 2
5 1 6 1 6 1 6 64 32
2) X dx X 2 0 0
0
6 0
6 6 6 3
9 9
1/ 2 x2 x1 / 2
3) 2X X 3 dx 2 3x
1
2 1/ 2 1
9
x2 2 x1 / 2 3x 1
9 2 12 2 91 / 2 11 / 2 39 1
80 4 24
52
Propiedades de las Integrales Definidas
Sea f una función integrable en a, b :
Propiedad 1:
b
f x dx 0 Es decir, si la base del área de la región bajo la curva es cero,
a
el área es cero.
Propiedad 2:
b
f x dx > 0 , x a, b y f(x) > 0, Es decir, el área de la región bajo la curva siempre
a
será positiva si f(x) es positiva.
Propiedad 3:
b
f x dx < 0, x a, b y f(x) < 0, Es decir, el área de la región bajo la curva siempre será
a
negativa si f(x) es negativa.
16

17. Propiedad 4:
c b c
f x dx = f x dx + f x dx , Si f es una función integrable en un intervalo que contiene
a a b
los puntos a, b, c talque a < b < c.
Propiedad 5:
b b b
f x g x dx f x dx g x dx Si f y g son funciones integrables en [a,b].
a a a
Propiedad 6:
b b
Kf x dx k f ( x)dx para toda constante k
a a
Propiedad 7:
b a
f ( x)dx = - f ( x)dx Al intercambiar los limites de integración cambia el signo de la
a b
integral.
Propiedad 8:
b b
f ( x)dx g x dx Si f y g son funciones integrables [a,b] y si f(x) g(x).
a a
Propiedad 9:
b
Kdx Kb a Es decir, si la función es constante su integral es el producto de la
a
constante por la diferencia de los límites de integración.
Ejemplos
Calcular la integral definida de las siguientes funciones:
17

18. 5
1) 7dx
2
5
Solución : como es una constante, entonces: 7dx = 7(5-2) = 7(3) = 21 (Por prop. 9)
2
2 2 2
2) x 3 dx 4 y x dx 2 entonces calcular 5x 3 3x 4 dx
0 0 0
Solución:
2 2 2 2
3 3
5x 3x 4 dx = 5 x dx 3xdx 4dx
0 0 0 0
2 2
5 x 3 dx 3 xdx 4 2 0
0 0
= 5(4) – 3(2) + 8 Sustituyendo
= 20 – 6 + 8
= 22
3) Calcular el área bajo la gráfica aplicando la integral definida.
4
3
2
1
1 2 3 4 5
Solución:
5
3dx 3(5 1) 3(4) 12u 2
1
18

19. 4) Evalúe
5 5
1 5 2 3
dx reescribimos x 5x dx
4 x2 x3 4
Solución:
5 5
2
x dx 5x 3 dx integrando obtenemos
4 4
1 2 5 5
x x 1 5
5
1 2 4
x 2x 2 4
Sustituimos aplicando la definición
1 5 1 5
2 2
5 25 4 24
1 5 1 5 17
= 0.10625
5 50 4 32 160
Ejercicios Propuestos
7
R/ = 2025/4
a) x3 4 x dx
2
6
R/ = -1661/12
b) y3 y 2 1 dy
5
R/ = 6
c) 3senZdz
0
19

20. 4
1 R/ = 8.2
d) x 3
x dx
1 x
e
R/ = 1
e) ln y dy
1
4
R/ = 192
f) 7x5/ 2 5 x 3 / 2 dx
0
0
3 R/ = 1/4
g) x 1 dx
1
8 R/ = 1/2
2
h) sec tdt
0
/4
R/ = 1/4
i) senx cosxdx
0
2
x R/ = 4/
j) cos dx
0
4
3
R/ = 23.37
k) xe x / 2 dx
1
2
x2 1
R/ = 3/2 e (e2-1)
l) 3xe dx
0
TEOREMA FUNDAMENTAL DEL CÁLCULO
Si f(x) es continua en el intervalo cerrado [a, b] y F es una primitiva de f en [a, b],
b
entonces a f x dx = F(b) – F(a); la diferencia F(b) – F(a) se denota por el símbolo f ( x)] b
a
o por F ( x) b .
a
Estrategia para usar el teorema fundamental del cálculo
1. Supuesta conocida una primitiva de f, disponemos de un nuevo recurso para calcular
integrales definidas que no requiere hallar el límite de una suma.
2. Use la siguiente notación para aplicar el teorema fundamental del cálculo
b
f ( x)dx = F ( x) a = F(b) – F(a).
b
a
Nota: No es necesario incluir una constante de integración C en la primitiva.
20

21. Ocurren los siguientes casos:
b a
1) Si a > b se tiene a
f x dx
b
f x dx
=- [F(a) – F(b)]
= F(b) – F(a)
2) a = b se tiene
a
f x dx 0 F a F a
a
Ejemplos
Evaluar
3
x3 3
a) 6x 2 5 dx 6 5x 2
2
3
3
2 x 3 5x 2
3 3
23 53 2 2 5 2
2 27 15 2 8 10
54 15 16 10
39 6
45
0
2x 3 3x 2 0
b) 2x 2 3x 2 dx 2x 2
2
3 2
3 2
2 2 03 02
2 3 22 2 3 20
3 2 3 2
21

22. 8
2 6 4 0
3
16 2
3 1
10
3
10
3
4 4 4 3/ 2 3/ 2
1/ 2 x3/ 2 4 4
c) 3 x dx 3 x dx 3 3 3 0
4 4
3/ 2 4
3/ 2 3/ 2
* Aplicación del teorema fundamental del cálculo para hallar un área.
d) Calcular el área de la región acotada por la gráfica f(x) = x2 en el intervalo 0,3 nótese
que y 2.
10
3
x3 3
9
Área = x 2 dx 0
.
0
3 8
33 0 3 7
6
3 3
2 5
9u
4
3
2
1
0
0,0 1,0 2,0 3,0 4,0
Nota: Este ejercicio esta resuelto al inicio de la unidad usando sumatoria.
TEOREMA DEL VALOR MEDIO PARA INTEGRALES DEFINIDAS
Si f es continua en el intervalo cerrado a, b , entonces existe un número “c” en a, b tal
b
que f ( x)dx f (c)(b a) , c puede ser cualquier punto de a, b .
a
22

23. Si despejamos f(c) tendríamos:
b
1
f (c ) f ( x)dx obteniéndose así la definición del valor medio de una función en un
b a a
intervalo cuyo teorema es:
“Si f es integrable en el intervalo cerrado a, b , el valor medio de f en a,b) es
b
1
f med f ( x)dx ”
b a a
Ejemplo
a) Halle el valor medio de f ( x) 3x 2 2 x en el intervalo 1,4 en este caso a =1, b = 4
b 4 4
1 1 2 1 3x 3 2x 2 1 3 4
f med f ( x)dx 3x 2 x dx x x2 1
b a a
4 11 3 3 2 1
3
1 3 2 3 2
4 4 1 1
3
1 1
64 16 0 48
3 3
16
GRAFICO
2
f(x) = 3x -2x
x Y
1 1
2 8
3 23
4 40
La figura muestra que el área de la región bajo la grafica de f es igual al área del
rectángulo cuya altura es el valor medio.
23

24. b) Encuentre un número c que satisfaga la conclusión del teorema del valor medio para la
3
siguiente integral definida x 2 dx f (c)(b a)
0
Recordemos que esta ya es un área conocida igual a 9 unidades cuadradas, por tanto
3
x 2 dx f (c)(b a)
0
x3 3
0 f (c ) 3 0
3
33
f (c)(3)
3
9 f (c)(3)
9
f (c )
3
f (c ) 3
Como f(x) = x2 entonces c2 = 3
c = 3 que es valor que satisface la conclusión del teorema.
INTEGRACIÓN NUMÉRICA
En varias ciencias, como las ciencias sociales, frecuentemente aparecen funciones en las
que se conocen de ellas solo su gráfica o algunos puntos de la misma. En estos casos no
es posible calcular la antiderivada de la función para determinar el área de la región
limitada por dicha función. Existe un método que proporciona una aproximación al valor
del área y que se conoce con el nombre de “INTEGRACIÓN NUMÉRICA”. Este método
se utiliza en los casos en que es muy complicado o imposible obtener la antiderivada de
la función.
Para aproximar el área de una región usaremos los siguientes métodos:
1) Método del Trapecio
24

25. Una forma de aproximar el valor de una integral definida es usar “n” trapecios como lo
muestra la figura:
x=0 x1 x2 x3 x4 = b
En este método se supone que f es continua y positiva en a, b de manera que la integral
b
f ( x)dx
a
representa el área de la región limitada por la grafica de f y el eje x, entre x=a y x=b.
b a
En primer lugar partimos a, b en n subintervalos, cada uno de anchura x tales
n
que a= x0 x1 x2 ... xn = b
A continuación formamos un trapecio sobre cada subintervalo como lo muestra la figura
f(x0)
f (x1)
x0 x1
25

26. b a
n
f xi 1 f ( x i ) b a
donde el área del i-ésimo trapecio = por tanto la suma de las áreas
2 n
de los n trapecios es:
b a f ( x0 ) f ( x1 ) f ( xn 1 ) f ( xn ) b a
Área = ... f ( x0 ) f ( x1 ) ... f ( xn 1 ) f ( xn )
n 2 2 2n
b b a
f ( x)dx f ( x0 ) 2 f ( x1 ) ... 2 f ( xn 1 ) f ( xn ) que es la regla del trapecio para
a 2n
b
aproximar a
f ( x)dx
Ejemplo:
3
1) Use la regla de los trapecio para estimar x 2 dx con n=5
0
b a 3 0 3
Primero calcular x
n 5 5
x0 0, x1 0.6, x 2 1.2, x3 1.8, x 4 2.4, x5 3
Segundo aplicar la ecuación
b a
= f ( x0 ) 2 f ( x1 ) 2 f ( x 2 ) ... 2 f ( x n 1 ) f ( x n )
2n
3 0
= 0 2(0.36 ) 2(1.44 ) 2(3.24 ) 2(5.76 ) 2(9)
2(5)
3
= 0.72 2.88 6.48 11.52 18 9.18 U 2
10
10
9
y = x2
A = 9.18 u2
8
7
6
5
4
3
2
1
26
0
0,0 1,0 2,0 3,0 4,0

27. 2) Use la regla del trapecio para estimar senxdx con n=4 y n=8
0
b a 0
Cuando n=4 x
n 4 4
3
x0 0, x1 , x2 , x3 , x4
4 2 4
0 3
senxdx sen0 2sen 2sen 2 sen 2sen
0 2(4) 4 2 4
2 2 2 1
= 0 2( ) 2(1) 2( ) 0 2 2 2 2 2 2 1.896
8 2 2 8 8 4
0
Cuando n=8 x
8 8
3 5 3 7
x0 0, x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8
8 4 8 2 8 4 8
0
senxdx sen0 2sen 2sen 2sen3 2sen 2sen5 2sen3 2sen7 sen
0
28 8 4 8 2 8 4 8
GRAFICA
como vemos
sen sen7 y sen3 sen5
8 8 8 8
Por tanto tenemos
27

28. 2 2
2sen 2 2sen3 2(1) 2sen5 2 2sen7
16 8 2 8 8 2 8
2 2 2 2 sen 2sen7 2sen3 2 sen5
16 8 8 8 8
2 2 2 4 sen 4sen3
16 8 8
Utilizando la calculadora obtenemos 1.974 u2 que se aproxima al área exacta que es 2u2
Ejercicios Propuestos
Aproxime el valor de la integral para el “n” que se especifique usando la regla del
trapecio.
2
2
R/ = 8/3 u2
a) x dx, n 4
0
8
2
R/ = 416/3 u2
b) 4 x dx, n 4
0
9
R/ = 38/3 u2
c) x dx, n 8
4
3
1 R/ = 2/3 u2
d) dx, n 4
1 x2
1.1
2
R/ = 0.089 8.9 * 10-2
e) senx dx n 4
1
28