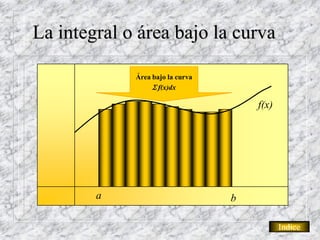
El documento resume los conceptos básicos de la integral definida y algunos de sus teoremas fundamentales. Explica que la integral definida representa el área bajo una curva y que puede calcularse como la suma de pequeñas áreas. También resume el Teorema Fundamental del Cálculo, el cual establece que la integral de una función es igual a la evaluación de su primitiva entre los límites, y que la derivada de una primitiva es la función original. Por último, explica que resolver integrales numéricamente implica aproximarlas como sumas, mientras que resolverlas

1. La integral
•Llyne Agudo

2. La integral definida
 El producto del valor
de la función en un
f(x)
punto, por la duración
del instante de
variación corresponde
f(x)dx con el concepto más
simple de integral.
dx
 Haz el instante tender
x
a cero y será dx.

3. La integral o área bajo la curva
Área bajo la curva
 f(x)dx
f(x)
a b
Indice

4. Definición de integral definida
La integral definida de la función f de a a b es el
número: n
I P 0
lim f ( x )xi
*
i
i 1
Que corresponde a la suma de n barras de ancho
x, donde este ancho se hace tan pequeño como se
quiera y x*i es un punto interior en cada barra.
|P| identifica el máximo ancho de todas las barras.
Indice

5. Teorema fundamental del Cálculo
 La primera parte de  Segunda parte: si G es
este teorema afirma cualquier primitiva de
que si F (la primitiva) f en [a,b], entonces:
corresponde a la b b
integral de una
función f, luego:
 f ( x)dx  G( x)  G(b)  G(a)
a a
 F’(x)=f(x)  ¡Conocida la
 Esto es: La derivada primitiva, únicamente
es la operación se evalúa en a y b.!
inversa de la integral.
Indice

6. Razonamiento básico
 El pretender resolver un problema que
implique una integral por métodos
numéricos, es equivalente a realizar una
suma que entre más términos tenga será más
exacto el resultado.
 Resolver integrales por métodos analíticos,
es equivalente a encontrar primitivas o
también llamadas antiderivadas.
Indice