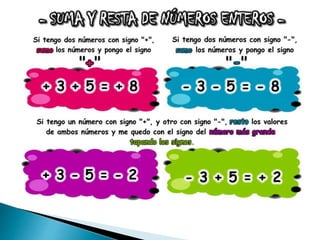
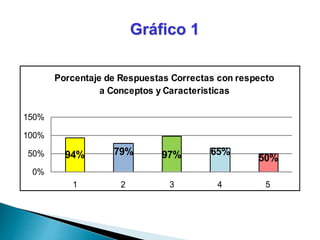
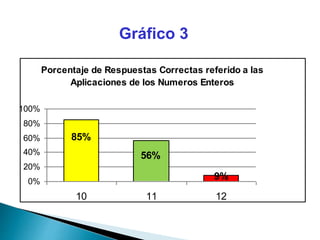
Este documento describe los números enteros, incluidas sus características, representación, operaciones básicas como suma, resta, multiplicación y división, y reglas para combinar operaciones. Explica cómo multiplicar y dividir números enteros siguiendo pasos específicos y proporciona ejemplos. También menciona que las raíces cuadradas de números negativos no tienen solución en los números reales y son números imaginarios. Finalmente, incluye gráficos sobre los resultados de una encuesta relacionada con conceptos de números enteros.

2. CONCEPTOS Y CARACTERÍSTICAS
 El conjunto de los números enteros se
describe como:
z = { ∞, …, -3, -2, -1, 0, 1, 2, 3, … ∞}
Representación gráfica de los números enteros:

4. OPERACIONES CON NÚMEROS ENTEROS
 Las operaciones básicas que podemos
realizar con los números enteros son las
siguientes:
 Suma
 Resta
 Multiplicación
 División

6. MULTIPLICACIÓN Y DIVISIÓN DE NÚMEROS ENTEROS
MULTIPLICACIÓN DE NÚMEROS ENTEROS
 Para multiplicar dos números enteros se siguen estos pasos.
 1.º Se multiplican sus valores absolutos (en la práctica, los números entre sí).
 2.º Al resultado le colocamos el signo + si ambos números son de igual signo, y el
signo − si son de signos diferentes
EJEMPLO: (+5) ⋅ (−3) = −15  5 ⋅ 3 = 15
El resultado es −15 ya que son de distinto signo (positivo y negativo).
(+5) ⋅ (+3) = +15  5 ⋅ 3 = 15
El resultado es +15 ya que son de igual signo (positivo)
DIVISION DE NÚMEROS ENTEROS:
 ¿Es posible? Claro que si! Se entiende como “ENTERO” porque no tienen parte decimal, y se
debe tener la siguiente salvedad , sólo se pueden dividir si el dividendo es múltiplo del
divisor y luego si se tratara de números primos, lo son únicamente por la unidad y por si
mismos.

7.  Son operaciones inversas.
 Se aplica la regla de los signos.
 Caso Particular: Raíz Cuadrada Negativa.
Las raíces de números negativos No tienen
Solución en el campo de los números reales
La solución es un numero imaginario.

8. COMBINACIÓN DE OPERACIONES
Para resolver operaciones combinadas
es indispensable seguir estas reglas:
 Primero se resuelven las operaciones que haya
entre paréntesis, corchetes y luego las llaves.
 Se resuelven las multiplicaciones antes que las
sumas y restas.
 Si hay un signo negativo anterior a los
paréntesis, corchetes y llaves, los signos de las
operaciones internas deben modificarse.

9. Gráfico 1
Porcentaje de Respuestas Correctas con respecto
a Conceptos y Caracteristicas
94% 79% 97% 65%
50%
150%
100%
50%
0%
1 2 3 4 5

10. Gráfico 2
Porcent aje de Respuest as Cor rect as con respect o a Propiedades y
Regla de los Signos
85%
24%
32% 32%
100%
80%
60%
40%
20%
0%
6 7 8 9
6
7
8
9

11. Gráfico 3
Porcentaje de Respuestas Correctas referido a las
Aplicaciones de los Numeros Enteros
9%
56%
85%
100%
80%
60%
40%
20%
0%
10 11 12

12.  Fue acertado el Diagnostico, el curso conoce lo
suficiente en cuanto a la naturaleza de este
conjunto de números, las aplicaciones y algunas
propiedades.
 Ventajas de la encuesta, al ser de opción múltiple y
devolver variables cualitativas no hubo muchos
inconvenientes en la tabulación.
 Desventajas: ausencia de ejercicios prácticos y
algún ejemplo numérico por ejemplo en las
preguntas 4, 8,9 y 12.

13.  A las Autoridades y Docentes del
Profesorado de Matemáticas que participan
del proyecto.
 A la profesora Ana María Gamboa.
 Se hace extensivo a cada uno de los alumnos
que participaron de la encuesta y por sus
valiosas devoluciones en los foros.
 A las familias por apoyar a cada uno durante
los encuentros en grupo.